
中国科学技术大学物理学院叶邦角整理 第32届全国中学生物理竞赛决赛理论考试评分标准 本卷可能需要用到下列公式: 广空-h:会-2+c:n+小-亏hx1 一、(15分)一根轻杆两端通过两根轻质弹簧A和B悬挂在天花 板下,一物块D通过轻质弹簧C连在轻杆上:A、B和C的劲度 系数分别为k、k,和k,D的质量为m,C与轻杆的连接点到A 和B的水平距离分别为α和b;整个系统的平衡时,轻杆接近水 平,如图所示。假设物块D在竖直方向做微小振动,A、B始终 6 可视为竖直,忽略空气阻力。 (1)求系统处于平衡位置时各弹簧相对于各自原长的仲长: (2)求物块D上下微小振动的固有频率: (3)当a和b满足什么条件时,物块D的固有频率最大?并求 Dm 出该固有频率的最大值。 参考解答: (1)沿竖直方向建立如图所示的坐标轴o.x。设三根弹簧 A、B和C的原长分别为1、1,和1,不妨设1,>1。设系 统处于平衡位置时,三根弹簧A、B和C相对于各自原长 的伸长分别为△x,、△x,和△x,。此时物块D处于平衡状态; 有 mg=k,△x3 即 4 ② AXE k E 设此时弹簧A和B的末端对轻杆的拉力分别为F和 mg £,。以弹簧C与轻杆的连接点为支点,由力矩平衡有 Fa=Fb ③ 竖直方向轻杆所受合力为零,有 F+F-mg=0 ④ 由胡克定律有 F=k△r ⑤ F2=k2△x ⑥ 由③④⑤⑥式得 4此-mgb ⑦ (a+b)k 11g0 △x,=(a+bk, ⑧ (2)挂上物块D之前,系统平衡时弹簧C的木端E点的坐标x为 x=(+4+) ⑨ a+b 挂上物块D后,系统重新处于半衡位置时,弹簧C的木端从E点移动到E'点。E点的坐 标x为 x=+A+h+△x3+a+A-4x) ⑩ a+b 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 将系统视为一等效弹簧,则系统处于静平衡时等效弹簧仲长为 AX:=x=A+r +a(r,Ar) ① a+b 将②⑦⑧式代入①式,得到系统处于静平衡时等效弹簧的伸长为 Axr =mg(a'k +bk)mg 1② (a+b)kk,k 因此等效弹簧的等效劲度系数为 (a+b)'kk k ③ a'k k+b'kk+(a+b)'k k 系统的固有频率为 (a+b)k kks .=mmlakkj+bk.k,+(a+b)'k.k:] ④ (3)由4@=0,有 da a=点6 ③ k 此时 d'=_m 6 da' (k+k)k+飞+k) 因此⑤式为系统尚有频率取最人值的条件,其最人固有频率的值为 (k+k2)ks 0三 ① (k+kz +k)m 评分标准: 第(1)问8分,①2③④⑤⑥⑦⑧式各1分 第(2)问4分,①②3④式各1分: 第(3)问3分,⑤⑥①式各1分. 二、(20分)如图,轨道型电磁发射器是山两条平行固定长直刚性金属导轨、高功率电源、 接触导电性能良好的电枢和发射体等构成。电流从电流源输出,经过导轨、电枢和另~条导 轨构成闭合回路,在空问中激发磁场。载流电枢在安培力作用下加速,推动发射体前进。已 比枢质量为m,发射体质量为m,:导轨单位长度的比阻为R,导轨每增加单位长度整个 回路的电感的增加量为,;电枢引入的电阻为R、电感为L,;回路连线引入的电阻为R,、 电感为L。导轨与电枢间摩擦以及空气阻力可忽略。 (1)试画出轨道型比磁发射器的等效比路图,并给出回路方程: (2)求发射体在导轨屮运动加速度的大小与可路电流的关系: (3)设回路比流为恒流I(平顶脉冲地流)、电枢和发射休的总质量为m,+m。=0.50kg、 导轨长度为x=500m、导轨.上单位长度电感增加量L,=1.0H/m,若发射体开始时静止, 山口速度为vm=3.0×103m/s,,求回路电流1和加速时间x。 中国科学技术大学物理学院叶邦角整理
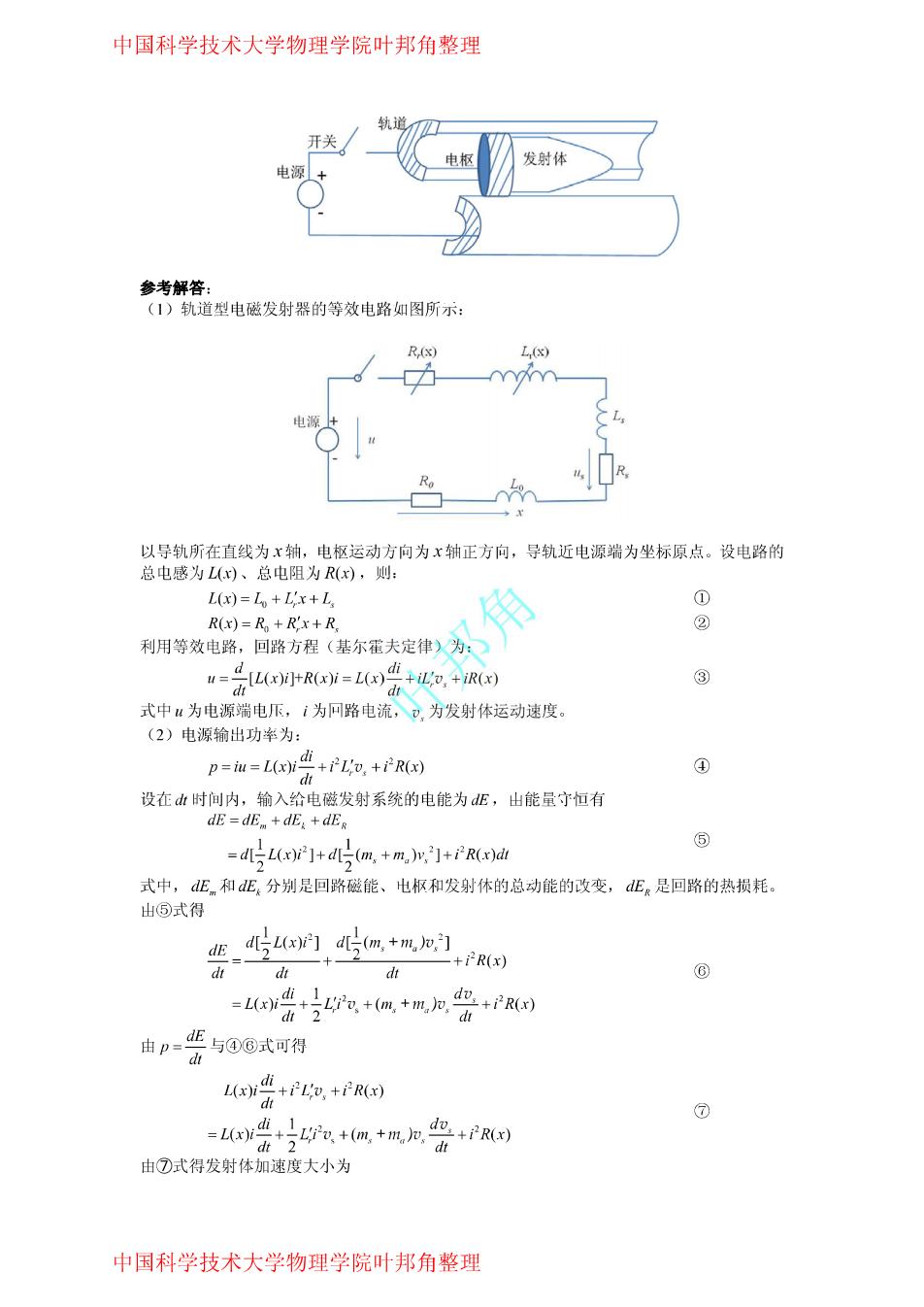
中国科学技术大学物理学院叶邦角整理 轨道 开关 电枢 发射体 电源 参考解答: (1)轨道型电磁发射器的等效电路如图所示: R(x) L,(x) 以导轨所在直线为x轴,电枢运动方向为x轴正方向,导轨近电源端为坐标原点。设电路的 总电感为L(心)、总电阻为R(x),则: L(x)=Lo+L'x+L ① R(x)=R+Rx+R ② 利用等效电路,回路方程(基尔霍夫定律)为: u=4L(x)i+R(x)i=L(x)+iL,+iR(x) ③ d dt 式中u为电源端电压,i为回路电流,。,为发射体运动速度。 (2)电源输出功率为: p=iu=L)i +2Lo,+R(x) ④ dt 设在d山时间内,输入给电磁发射系统的电能为dE,山能量守恒有 dE =dE+dE+dEg ⑤ -dL()]+d (m+m)v,]+R(x)di 式中,dE和dE分别是回路磁能、枢和发射体的总动能的改变,dE。是回路的热损耗。 出⑤式得 dE d5L(x)]d5m,+,力,] +2R(x) d dt dt ⑥ =L(x)idi 1 +'0,+(m,+m,加, dt 2 do+i平R(x) 由p=E与④⑥式可得 L)i+PL+PR() dt =L)idi1 ⑦ 而++m+m,加多+ dt 由⑦式得发射体加速度大小为 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 1 、L2 ⑧ dt2(m、+m (3)若回路电流为恒流I,则电枢和发射体在时刻1的加速度、速度和位移的大小分别为 a=d地= 1 LP dt2(m。+m,) ⑨ L12 0、=a,f= ⑩ 2(m。+m,) 1 L72 x=21= 一2 ① 4(m。+m,) 要使发射体山口速度m达到3.0×103ms,则由题给数据得 9.0×10 dom= m/s2=9.0×103ms3 1② 2Xsm 2×5.0 H⑨2式得 2(m。+ma)am 2×0.50×9.0×106 A=3.0×10°A L 1.0×10-6 加速时间为 T=D=3.0x103 s=3.3×10-4s ④ am9.0×105 评分标准:第(1)问7分,等效电路图正确给3分,①②式各1分,③式2分: 第(2)问8分,④⑤⑥式各2分,⑦⑧式各1分: 第(3)问5分,⑨⑩①3④式各1分。 二、(15分)俄国火箭专家齐奥尔科夫斯基将火箭发射过程进行模型简化,得出了最早的理 想火箭方程,为近代火箭、导弹T程提供了理论依据。该简化模型为:待发射火箭静止于惯 性参考系S中某点,忽略火箭所受的地球引力等外力的作刀,火箭(包含燃料)的初始静 止质量为M,;在=0时刻点火,火箭向左排出气休,气体相对于火箭的速度恒为'。,使火 箭向右发射:在S系中观测,火箭的速度为,排出气体的速度为V,,如图所示。根据此 模型,火箭运行一段时间后,当其静止质量山M,变为M时, (1)用牛顿力学推导火箭所获得的速度V与质量比M/M,之间的关系: (2)用狭义相对论力学推导火箭所获得的速度Y与质量比M/M,之间的关系: (3)当Y远小于真空中的光速c时,计算以上两种结果之差,保留至(化/c)项。 V(相对丁火箭) '(相对于S系) (相对于S系) M 参考解答: (1)用牛顿力学求火箭获得的速度与质量比率之间的关系。 根据动量守恒定律,火箭动量的变化等于排出质量为dm的气体引起的动量的变化 d(MV)=V,dm ① 由质量守恒定律得 dMdm =0 ② 由速度叠加原理有 2='。- ③ 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 将③式代入①式得 d(M')=('-')dm ④ 将②式代入④式得 dM=_dy ⑤ M V. 两边取积分得 此兴 ⑥ 利用题给积分公式完成积分,并考虑初始条件,得 n-上 ⑦ M,' 或 M y=-'ln。 ⑧ “M (2)用狭义相对论求火箭获得的速度与质量比率之间的大系。 根据相对论动量守恒定律,火箭动量的变化等于排出质量为dm的气体引起的动量变化 d MV )= dm ⑨ v1-V2/c v1-V2/c2 根据相对论能量守恒定律,火箭能量的减少等于排山质量dm的气休对应的能量 Me2 an-vl dme2 ⑩ 邦角 V1-1c 中相对论速度叠加原理有 y。- V,=1-W.19 ① 将①式代入⑨式并利用⑩式得 d(- d(- ② 1-1c 1-vV.lc;-v2lc 此即 dM dv 图 MV.1-V21c2) 对③式两边积分,并利用恒等式 品) 1 得 兴e ④ 利用题给积分公式完成积分,并考虑初始条件,得 5 或 6 或 5=1-(M/M)ě 1+M/M)产 ⑩ 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 (3)当火箭速度?很小时,利用公式 ln(1+x)≈x- ,当x<1 2 得 1+)-和n--之-j 1⑧ 把⑧代入用相对论力学求得的结果⑤式,并利用⑧式,得 n)- 丽 -wH}-o】 可见,在火箭速度很小的情况下,相对论力学的结果与牛顿力学的结果之差直至 级为零,实际上为 的量级。 评分标准:第(1)问5分,①②③⑤⑦[或⑧]各1分: 第(2)问8分,⑨式2分,⑩式1分,①式2分,飞④⑤[或⑤或①]式各1分: 第(3)问2分,⑧9式各1分。 四、(15分)光在物体表面反射或者被吸收时,光子将其动堂传给物休,使光具有对物体的 辐射压力(光压)。利而光压,可实现对某些微小粒子的精确操控(光镊)。设在≥L的区 域有一匀强激光场,沿z轴负方问入射,其强度(单位时间内通过单位横截面积的光能)为 I;在y∈(-L,L)之间没有光场,其横截面如图所示。一密度为p的三棱柱形小物体(其横 截面是底边长为2L、底角为O的等腰三角形)被置于光滑的水平面y上,其朝上的A和B两 面均涂有特殊反射层,能完全反射入射光。小物体初始时静止,位置如图。 (1)假定光子的反射角等于入射角,H反射前后光子的频率不变。试求: (a)小物体在受到激光场照射后的动力学方程; (b)小物体从初始位置向y轴负方向移动3L2的距离所需的时间。 (2)实际上,由于小物体的运动,反射光了频举会有微小的变化:在小物体从初始位置向 y轴负方向移动到距离为3L/2的过程中,定性比较反射光子与入射光子频率的大小及其随时 间的变化。 B 参考解答: (1) (a)先计算母个光子对于物体的作用。假定光的频率是v,树个光子的能量和动量大小分 别为 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 Eo=hv ① hi ② 现分析光子反射后相对于反射前共动量的变 化量。如z剖面图所示,光子入射到B面的入射 角和反射角都等于等腰三角形的底角日,出射光子 的动量方向与z轴成20角:由题设,山射光子动 Po 量的大小在反射前后基本不变。光子反射给物体的 冲量在z轴方向的分量与xy平面的支持力抵消, 其在x轴的分量为零,只有在y轴上的分量不为零: 且y平面光滑,所以物体只会沿y轴做水平运动。 Q0,y,0) 故可以用等腰三角形顶点在y轴上的垂足Q(0,y,0) 变化米表征整个物体的运动。单个光子在B面上反射后给物体的冲量沿y轴的分量大小 为 1osin20 ③ 方向指向坐标原点O。 再计算当Q(0,y,0)点处在y轴的止半轴上不同位置即y≥0时,单位时间内入射到斜面 B上的光了数。这时,激光束入射到物体的B面,其横截面积为 s=yd ④ 其中,为该二棱柱形小物体的棱长。此时物体受到的单位时间内的激光的入射功率为 w=Is lyd ⑤ 此时单位时间内入射物体B面的光子数为 n="-d ⑥ Eo hv 同理,当Q(0,y,0)点处在y轴的负半轴上即y≤0时,单位时间内入射到物体的A面的光子 数为 n=”=-d ⑦ Eo hv 由于光束反射给物体带来的力的z轴分量以及物体本身的亚力始终与y平面的支持力 抵消,同时山③式中的单个光子反射后给物体带来的冲量的y轴分量大小并考虑到其方向指 向坐标原点,所以物体受到的合外力F与物体上Q(0,y,0)点的y轴坐标y的关系为 F=nloy = Id sin20 1V ⑧ 这是一个线性回复力。 出⑧式可知,物体从初始位置丌始、在受到中空激光场照射后,以坐标原点为中心沿着 y轴做简谐运动,对应的谐振动角频率为 Id sin20/c 2Icos20 0= ⑨ VoL'dtan0 Cpl 考虑到Q(0,y,0)点的初始位置为(0,L,0),物体上Q(0,y,0)点的运动方程为 Lcos 21 cos0 cpl2 ⑩ ()小物体从初始位置向y抽负方向移动3汇2的距离的时候)=-,考虑到@式,则 21 cos20 -L=Lcos ① cpL☑ 小物体从从初始位置向y轴负方向移动3L/2的距离的时间为 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 2πL 1= 3cos0121 ② (2)当小物体从题图的初始位置开始向y轴负方向移动到距离为L的过程中,由」反射光 子速度的y分量与小物体的运动方向相反,根据多普勒效应,反射光子的频率比入射光子的 频率小;随着时间的增加,反射光子的频率会越来越小(即与入射光子的频率的差距越来越 大)。 当小物体继续向y轴负方向移动到离初始位置的距离为3L/2的过程中,由」反射光子 速度的y分量与小物体运动方向相同,根据多普勒效应,反射光子的频率比入射光子的频率 大;随着时间的增加,反射光子的频率会越米越小(即与入射光子频率差距越米越小)。 评分标准:第(1)问11分,①式1分,②式2分,③④⑤⑥⑦⑧式各1分,描述出“物体 从题设图示的初始位置开始在受到巾空激光场照射后以坐标原点为巾心沿着y轴做简谐运 动”这一结论或者直接得到⑩式给1分,②式1分:第(2)问4分,准确判断山两种情况下 反射光子频率小或大各1分,准确判断出两种情况下反射光子频率的变化趋势各给1分。 五、(20分)如图,一个上端固定、内半径为R的 玻璃圆筒底部浸没在人容器中的水而之下,未与容 器底接触:另将一个外半径为R,(R,略小于R,) 2 的同质玻璃制成的圆筒(上端固定)放置其中,不 接触容器底,保持两玻璃圆简的中轴线重合且竖 直。设水与玻璃之间的接触角为0(即气-液界面在 水的最高处的切线与固液界面的夹角,见局部放大 图)。已知水的表面张力系数为α,地面重力加速 度大小为g。 (1)在毛细现象中,系统毛细作用引起的势能变 化,可以等效地看作山-液-气分界线上液体表面张 力在液面上升或下降过程中做的功。试证:以大容 器中的水面处为系统势能零点,则当水由于毛细作用上升高度为h时,系统毛细作用的势能 为 E(h)=-2xacos0(R+R)h: (2)试导出系统在水由于毛细作用上升的过程中释放的热量: (3)如果在超力米高空飞机中短时间内做此实验,飞机可视为做匀速直线运动。测得该系 统在同样过程中放出的热量为Q,试求此时飞机距离地面的高度。假定该飞机内水的表面张 力系数和接触角与地面情形相问。 以上计算不考虑地球的自转。 参考解答: (1)作用在两筒壁之问的水面与玻璃壁的交界线上水面的表面张力沿器壁方向的投影F的 大小为 F。=2πR,acos0+2πR,acos0 ① 该力大小不变,方向竖直向下。当水由于毛细作用上升到相对于大容器中的水面高度为时, 力F所做的功为 W=-Fh ② 系统毛细作用引起的势能变化为 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 E(h)-E(0)=W ③ 式中,E,(O)是系统毛细作用的势能在h=0处的值。由题设有 E,(0)=0 ④ 联立①②③④式得 E.(h)=-2za cose(R +R,)h ⑤ (2)两圆筒之间水面上升h时引起的重力势能的改变为 E。=Pg(xR-πR)h ⑥ 联立⑤⑥式,可知系统达到平衡时的系统毛细作用的总势能为 E()=E(h)+Eo(h)=pg(R-R)h-2racos(+R:)h ⑦ 根据系统平衡时势能最小原理 de(h =0 dh n=he 可知 pgh(R2-R)=2Racos0+2Racos0 ⑧ 系统平衡时,两圆筒之间水面上升的高度是 2acos0 h。= 邦角 ⑨ P8(R-R) 因此,在平衡时,中⑤⑥⑨式得 E,(h)=- 4πa2cos20(R+2) ⑩ Pg(R-R2) 2πa2cos20(R,+R,) Eg(he)= ① Pg(R-R,) 毛细作用势能的减小,一部分转化为水的重力势能,另一部分用来克服系统摩擦而做的功, 这部分的功转化为热耗散了。因此,系统平衡时释放的热量为 Q=[-E(h】-Ec(h) @ 出⑩①②式得 Q=2xa'cos'0(R+R.) ⑧ p8(R-R2) (3)设飞机处在距离地球地面高度:处,根据 mg: ®*,8 GMm ④ R电 式中R为地球半径,G为万有引力常数,M为地球质量。可得重力加速度随地面高度的 变化规律为 g 8,-0+z1R} ⑤ 将⑤式代入③式,可得在地球不同高度处,所释放的热量随高度的变化关系为 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 Q=2za'cos0(R+R ⑥ p8(R-R2) 飞机距离地球地血高度z为 z=R地 Qpg(R-R2) -1 ① V2πa2cos20(R+R2) 评分标准:第(1)问5分,①式2分,②③④式各1分: 第(2)问10分,⑥式2分,⑦⑧⑨⑩①式各1分,②式2分,③式1分: 第(3)问5分,④式2分,⑤6①式各1分。 六、(15分)太阳系内行星的公转方向是基本相问的。地球上的观测者所看到的行星位置实 际上是该行星在遥远的背景星空中的投影。山于各行星的公转速度以及它们在轨道上位置的 不同,地球上的观测者看到的行星在背景星空中移动的方向与地球的公转方向并非总是相 同。人们把看到的行星移动方向与地球公转方向相同情形下行星的视运动叫顺行,方向相反 的叫逆行。当行星位于由顺行转为逆行或由逆行转为顺行的转折点时,行星看起来好像停留 在星空不动,该位置叫留。天义学把地外行星运行到太阳和地球所在的直线上、且太阳和地 外行星位于地球两侧的情形叫行星冲日。火星冲日是常见的天文现象。设地球和火星都在同 :平面内绕太阳做圆周运动,且只考虑太阳对行星的引力。已知火星轨道半径R为地球轨 道半径R的1.524倍,不考虑地球的自转,试计算火星在经历相邻两次冲日的时问问隔内其 视运动为逆厅和顶行的时间间隔。 参考解答: 选如图所示地球、火星和太阳三点共线(火星冲日) 时为计时零点,逆时针方向为中角的正方向。经过时间t后, 火星在如图所示的以地心为原点的平动坐标系0y中的位 烈火星 置为: x=Rm cos @mt-Ro cos @ot ① -x y=R sin @t-Ro sin @ot ② 太阳 地球 0m和@,分别为火星和地球的公转角速度。火星与地球的 连线在地球坐标系0-y中与x轴的夹角中为 tan- R sin @t-Ro sin @ot ③ R cos @t-Ro cos aot ③式两边对时问求导,得 p=0R+4R-(@m+4)RR cos[(-0)]川 ④ cos2 (Rm cos @t-Ro cost) 火足的顺行或逆行分别对应中为正或为负的情形。令中=0,有 @mRmn +@oRo-(a+a)R Ro cos[(a-a )t]=0 ⑤ 解得 1 t=土 R+oRo -arccos- ⑥ 0,-0m (+)R Ro 火星在经历相邻两次冲日的时间间隔内,仅当 0nR+0R时 1 arccos 0R+,R时 0-0m (Om +)RRo @o-cm (0m+⊙,)RR 中国科学技术大学物理学院叶邦角整理