
中国科学技术大学物理学院叶邦角整理 第28届全国中学生物理竞赛复赛试卷 题号 二 三 四 五 六 七 八 总分 得分 阅卷 复核 说明: 填空题的答案填在题中的横线上或题给的表格中, 计算题的解答应写出必要的文字说明、方程式和重要的演算步骤,只写出最后结果 的不能得分.有数值计算的,答案中必须明确写出数值和单位 本卷共8题,满分160分. 一、(20分)如图所示,哈雷曹星绕太阳S沿椭圆轨道逆时针方向 得分 阅卷复核 运动,其周期T为76.1年.1986年它过近日点P。时,与太阳S的 距离。=0.590AU,AU是天文单位,它等于地球与太阳的平均距 离.经过一段时间,彗星到达轨道上的P点,SP与SP。的夹角 0p=72.0°.已知:1AU=1.50×10"m,引力常量C=6.67×10-m3.kg1.s2,太阳质 量ms=1.99×10kg,试求P到太阳S的距离r。及彗星过P点时速度的大小及方向(用 速度方向与SP。的夹角表示). 二、(20分)质量均匀分布的刚性 得分 阅卷复核 杆AB、CD如图放置,A点与水平 地面接触,与地面间的静摩擦系数 D 为4A,B、D两点与光滑竖直墙面 接触,杆AB和CD接触处的静摩擦系数为Hc,两杆的质量 均为m,长度均为l 1.已知系统平衡时AB杆与墙面夹角为0,求CD杆与 墙面的夹角α应该满足的条件(用α及已知量满足的方程 式表示) 2.若4=1.00,c=0.866,0=60.0°,求系统平衡 时α的取值范围(用数值计算求出)
1 中国科学技术大学物理学院叶邦角整理
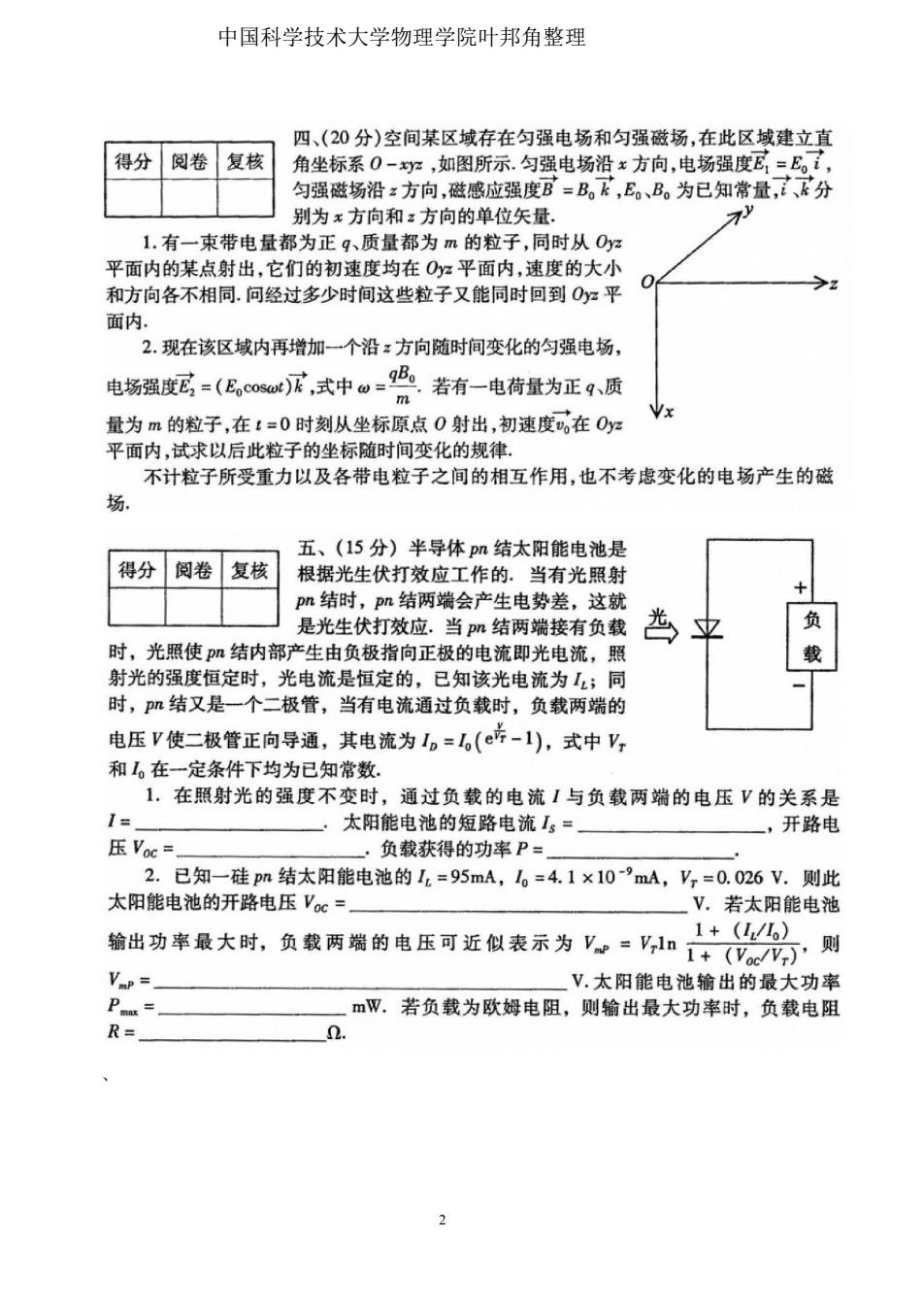
中国科学技术大学物理学院叶邦角整理 四、(20分)空间某区域存在匀强电场和匀强磁场,在此区域建立直 得分 阅卷 复核 角坐标系0-严,如图所示.匀强电场沿x方向,电场强度E,=E。, 匀强磁场沿:方向,磁感应强度B=B。下,E。、B。为已知常量,、分 别为x方向和:方向的单位矢量, 1.有一束带电量都为正g、质量都为m的粒子,同时从Oyz 平面内的某点射出,它们的初速度均在O:平面内,速度的大小 和方向各不相同.问经过多少时间这些粒子又能同时回到Oz平 面内. 2.现在该区域内再增加一个沿:方向随时间变化的匀强电场, 电场强度=(8,c正,式中。-识若有-电荷量为正g、质 x 量为m的粒子,在t=0时刻从坐标原点0射出,初速度在Oy 平面内,试求以后此粒子的坐标随时间变化的规律, 不计粒子所受重力以及各带电粒子之间的相互作用,也不考虑变化的电场产生的磁 场。 五、(15分)半导体pn结太阳能电池是 得分 阅卷 复核 根据光生伏打效应工作的.当有光照射 pn结时,pn结两端会产生电势差,这就 是光生伏打效应.当pn结两端接有负载 负 时,光照使p肌结内部产生由负极指向正极的电流即光电流,照 射光的强度恒定时,光电流是恒定的,已知该光电流为I;同 时,p结又是一个二极管,当有电流通过负载时,负载两端的 电压V使二极管正向导通,其电流为1。=,(e诉-1),式中V, 和。在一定条件下均为已知常数, 1.在照射光的强度不变时,通过负载的电流I与负载两端的电压V的关系是 I= 太阳能电池的短路电流I5= ,开路电 压Voc= 负载获得的功率P= 2.已知一硅pn结太阳能电池的1=95mA,。=4.1×10-’mA,V,=0.026V.则此 太阳能电池的开路电压Vc=」 V.若太阳能电池 1+(I/L) 输出功率最大时,负载两端的电压可近似表示为V0=,1n+(V,则 VP= V.太阳能电池输出的最大功率 mW.若负载为欧姆电阻,则输出最大功率时,负载电阻 R= 2
2 、 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 六、(20分)图示为圆柱形气缸,气缸壁绝热,气缸的右端有一小 得分 阅卷 复核 孔与大气相通,大气的压强为Po·用一热容量可忽略的导热隔板N 和一绝热活塞M将气缸分为A、B、C三室,隔板与气缸固连,活 塞相对气缸可以无摩擦地移 N M 动但不漏气.气缸的左端A室中有一电加热器D. 已知在A、B室中均盛有1摩尔同种理想气体,电加 A 热器加热前,系统处于平衡状态,A、B两室中气体 的温度均为T。,A、B、C三室的体积均为V。,现通 过电加热器对A室中气体缓慢加热,若提供的总热量为Q。,试求B室中气体末态体积和A 室中气体的末态温度, 设A、B两室中气体1摩尔的内能为U=7,式中R为普适气体常量,T为绝对温 度 3
3 中国科学技术大学物理学院叶邦角整理
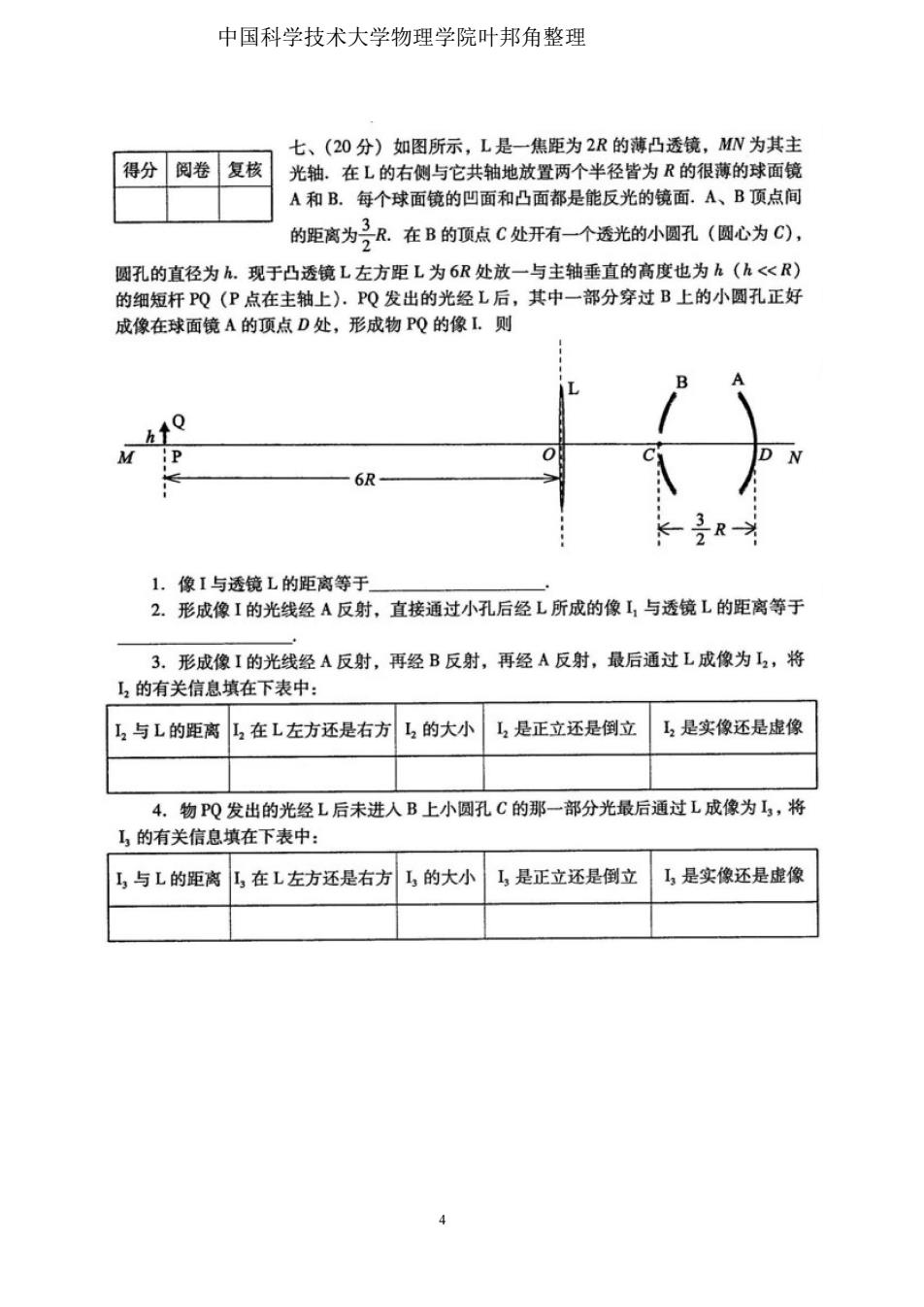
中国科学技术大学物理学院叶邦角整理 七、(20分)如图所示,L是一焦距为2R的薄凸透镜,MN为其主 得分 阅卷 复核 光轴。在L的右侧与它共轴地放置两个半径皆为R的很薄的球面镜 A和B.每个球面镜的凹面和凸面都是能反光的镜面.A、B顶点间 的距离为R、在B的顶点C处开有-个透光的小圆孔(圆心为C), 圆孔的直径为h.现于凸透镜L左方距L为6R处放一与主轴垂直的高度也为k(h<R) 的细短杆PQ(P点在主轴上).PQ发出的光经L后,其中一部分穿过B上的小圆孔正好 成像在球面镜A的顶点D处,形成物PQ的像L.则 P 0 6R 是R 1.像I与透镜L的距离等于 2.形成像I的光线经A反射,直接通过小孔后经L所成的像L,与透镜L的距离等于 3.形成像I的光线经A反射,再经B反射,再经A反射,最后通过L成像为I2,将 2的有关信息填在下表中: 2与L的距离 】2在L左方还是右方 L2的大小 马2是正立还是倒立 2是实像还是虚像 4. 物PQ发出的光经L后未进人B上小圆孔C的那一部分光最后通过L成像为J,将 L,的有关信息填在下表中: L3与L的距离 L,在L左方还是右方 ,的大小 L,是正立还是倒立 工,是实像还是虚像
4 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 八、(20分)有一核反应其反应式为p+H→He+n,反应中所 得分 阅卷 复核 有粒子的速度均远小于光速.试问: 1.它是吸能反应还是放能反应,反应能Q为多少? 2.在该核反应中,若H静止,入射质子的阈能T为多少?阈 能是使该核反应能够发生的入射粒子的最小动能(相对实验室参考系): 3.已知在该反应中入射质子的动能为1.21MeV,若所产生中子的出射方向与质子的 入射方向成60.0°角,则该中子的动能T.为多少? 已知p、0n、H核、2He核的静止质量分别为:m,=1.007276u,m。=1.008665u, m3g=3.015501u,m=3.014932u.u是原子质量单位,1u对应的能量为931.5MeV. 结果取三位有效数字, 参考解答: 解法一 取直角坐标系Oy,原点O位于椭圆的中心,则哈雷彗星的椭圆轨道方程为 x2.y2 =1 (1) a、b分别为椭圆的半长轴和半短轴,太阳S位于椭圆的一个焦点处,如图1所示 以T表示地球绕太阳运动的周期,则T=1.00年;以α.表示地球到太阳的距离(认为地球 绕太阳作圆周运动),则a.=1.00AU,根据开普勒第三定律,有 a T2 (2) 0 设c为椭圆中心到焦点的距离,由几何关系得 b C=a-0 (3) 人8p Po x J
5 参考解答: 解法一 取直角坐标系 Oxy,原点 O 位于椭圆的中心,则哈雷彗星的椭圆轨道方程为 2 2 2 2 1 x y a b (1) a、b 分别为椭圆的半长轴和半短轴,太阳 S 位于椭圆的一个焦点处,如图 1 所示. 以Te 表示地球绕太阳运动的周期,则 e T 1.00年 ;以 e a 表示地球到太阳的距离(认为地球 绕太阳作圆周运动),则 e a 1.00AU ,根据开普勒第三定律,有 3 2 3 2 a T a T e e (2) 设 c 为椭圆中心到焦点的距离,由几何关系得 c a r 0 (3) S P P Pr a b O P0 x y 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 b=va2-c2 (4) 由图1可知,P点的坐标 图1 x=c+rp cosep (5) y=rp sinep (6) 把(5)、(6)式代入(1)式化简得 (a'sin20p+b2 cos2 0p)re+2b2crp cos0p +b'c2-a'b2=0 (7) 根据求根公式可得 b2(a-ccosep) =a sin+b cos0 (8) 由(2)(3)、(4)(8)各式并代入有关数据得 p=0.896AU (9) 可以证明,彗星绕太阳作椭圆运动的机械能为 E=_Gmm, (10) 2a 式中m为彗星的质量.以)p表示彗星在P点时速度的大小,根据机械能守恒定律有 mo+ Gmms (11) 2a 得 21 ,-6ma (12) 代入有关数据得 vp=4.39×104ms (13) 设P点速度方向与SP的夹角为p(见图2),根据开普勒第二定律 rpopsin[o-0p]=20 (14) 其中σ为面积速度,并有 a=Tab P (15) T 6 由(9)、(13)、(14)、(15)式并代入有关数据可 人8 得 a S
6 22 cab (4) 由图 1 可知,P 点的坐标 cos P P x c r (5) sin P P y r (6) 把(5)、(6)式代入(1)式化简得 2 2 2 2 2 2 2 2 2 2 sin cos 2 cos 0 P P P P P a b r b cr b c a b (7) 根据求根公式可得 2 2 2 2 2 cos sin cos P P P P b a c r a b (8) 由(2)、(3)、(4)、(8)各式并代入有关数据得 rP 0.896AU (9) 可以证明,彗星绕太阳作椭圆运动的机械能为 s 2 Gmm E = a (10) 式中 m 为彗星的质量.以 P v 表示彗星在 P 点时速度的大小,根据机械能守恒定律有 1 2 s s 2 2 P P Gmm Gmm m r a v (11) 得 s 2 1 P P Gm r a v (12) 代入有关数据得 4 1 4.39 10 m s P v = (13) 设 P 点速度方向与 0 SP 的夹角为 (见图 2),根据开普勒第二定律 rP P P v sin 2 (14) 其中 为面积速度,并有 πab T (15) 由(9)、(13)、(14)、(15)式并代入有关数据可 得 S P P Pr a b O P0 x y 图 1 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 p=127° (16) 图2 解法二 取极坐标,极点位于太阳S所在的焦点处,由S引向近日点的射线为极轴,极角为日,取逆 时针为正向,用r、B表示彗星的椭圆轨道方程为 p = (1) 1+ecos0 其中,e为椭圆偏心率,p是过焦点的半正焦弦,若椭圆的半长轴为a,根据解析几何可知 p=a1-e2) (2) 将(2)式代入(1)式可得 al-e) r= (3) 1+ecos0 以T表示地球绕太阳运动的周期,则T=1.00年:以α.表示地球到太阳的距离(认为地球 绕太阳作圆周运动),则a.=1.00AU,根据开普勒第三定律,有 a T2 3 (4) a 在近日点0=0,由(3)式可得 e=1-6 (5) a 将Bp、a、e的数据代入(3)式即得 p=0.895AU (6) 可以证明,彗星绕太阳作椭圆运动的机械能 E=_Gmm, (7) 2a 式中m为彗星的质量.以⑦p表示彗星在P点时速度的大小,根据机械能守恒定律有 Gmm. Gmm (8) 2a 可得 21 Gm,'re d (9) 代入有关数据得 0p=4.39×104msl (10)
7 127 (16) 解法二 取极坐标,极点位于太阳 S 所在的焦点处,由 S 引向近日点的射线为极轴,极角为 ,取逆 时针为正向,用 r、 表示彗星的椭圆轨道方程为 1 cos p r e (1) 其中,e 为椭圆偏心率,p 是过焦点的半正焦弦,若椭圆的半长轴为 a,根据解析几何可知 2 p a e 1 (2) 将(2)式代入(1)式可得 1 cos 1 2 e ea r (3) 以Te 表示地球绕太阳运动的周期,则 e T 1.00年 ;以 e a 表示地球到太阳的距离(认为地球 绕太阳作圆周运动),则 e a 1.00AU ,根据开普勒第三定律,有 3 2 3 2 a T a T e e (4) 在近日点 0 ,由(3)式可得 1 r e a 0 (5) 将 P 、a 、e 的数据代入(3)式即得 rP 0.895AU (6) 可以证明,彗星绕太阳作椭圆运动的机械能 s 2 Gmm E = a (7) 式中 m 为彗星的质量.以 P v 表示彗星在 P 点时速度的大小,根据机械能守恒定律有 1 2 s s 2 2 P P Gmm Gmm m r a v (8) 可得 2 1 P s P Gm r a v (9) 代入有关数据得 4 1 4.39 10 m s P v = (10) 图 2 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 设P点速度方向与极轴的夹角为Q,彗星在近日点的速度为)。,再根据角动量守恒定律, 有 rpvp sin(p-0p)=rvo (11) 根据(8)式,同理可得 vo=Gm, 21 (12) 由(6)、(10)、(11)、(12)式并代入其它有关数据 p=127 (13) 评分标准: 本题20分 解法一 (2)式3分,(8)式4分,(9)式2分,(11)式3分,(13)式2分,(14)式3分,(15) 式1分,(16)式2分. 解法二 (3)式2分,(4)式3分,(5)式2分,(6)式2分,(8)式3分,(10)式2分,(11)式 3分,(12)式1分,(13)式2分. 二、参考解答: 1.建立如图所示坐标系Oxy.两杆的受力情况如图: ∫为地面作用于杆AB的摩擦力,N,为地面对杆AB 的支持力,∫)、N2为杆AB作用于杆CD的摩擦力和支持 D N4 力,N,、N,分别为墙对杆AB和CD的作用力,mg为重 力.取杆AB和CD构成的系统为研究对象,系统平衡时,由 平衡条件有 ☑BN mg N4+N3-f=0 (1) N1-2mg=0 (2) 以及对A点的力矩 6
8 设 P 点速度方向与极轴的夹角为 ,彗星在近日点的速度为 0 v ,再根据角动量守恒定律, 有 r r P P P v v sin 0 0 (11) 根据(8)式,同理可得 2 1 Gms r a 0 0 v (12) 由(6)、(10)、(11)、(12)式并代入其它有关数据 127 (13) 评分标准: 本题 20 分 解法一 (2)式 3 分,(8)式 4 分,(9)式 2 分,(11)式 3 分,(13) 式 2 分,(14)式 3 分,(15) 式 1 分,(16)式 2 分. 解法二 (3)式 2 分,(4)式 3 分,(5)式 2 分,(6)式 2 分,(8)式 3 分,(10) 式 2 分,(11)式 3 分,(12)式 1 分,(13)式 2 分. 二、参考解答: 1.建立如图所示坐标系 Oxy.两杆的受力情况如图: 1 f 为地面作用于杆 AB 的摩擦力, N1为地面对杆 AB 的支持力, 2f 、 N2 为杆 AB 作用于杆CD的摩擦力和支持 力, N3 、 N4 分别为墙对杆AB和CD的作用力,mg 为重 力.取杆AB和CD构成的系统为研究对象,系统平衡时, 由 平衡条件有 4 3 1 N N f 0 (1) 1 N mg 2 0 (2) 以及对 A 点的力矩 B D C A N1 E N2 mg mg f2 F O y f1 N4 N3 x 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 IsinO-Isina-No ()0 1 2 即 mlsin-mg/sina-N,lcos0-N,(lcos0lc-CF)-0 (3) 式中CF待求.F是过C的竖直线与过B的水平线的交点,E为BF与CD的交点.由几何关系 有 CF=Isinacot0 (4) 取杆CD为研究对象,由平衡条件有 N+N2 cose-f,sin=0 (5) N,sin0+f,cose-mg =0 (6) 以及对C点的力矩 1 N.I cosa-mglsina0 (7) 解以上各式可得 1 N=mg tan a (8) N3 tane-Itana-tanasina mg (9) cose 2 sine stano_sind I tancsina (10) cose 2 sine mg N=2mg (11) in-tancco mg (12) cos0+-tanasin mg (13) CD杆平衡的必要条件为 3≤4.N2 (14) 由(12)、(13)、(14)式得 2(uc sin0-cos) tana≤ (15) 4ccosθ+sin0 AB杆平衡的必要条件为 9
9 3 4 1 1 sin sin sin cos cos cos 0 2 2 mgl mg l l N l N l l CF 即 3 4 3 1 sin sin cos cos cos 0 2 2 mgl mgl N l N l l CF (3) 式中CF 待求. F 是过C 的竖直线与过 B 的水平线的交点, E 为 BF 与CD 的交点.由几何关系 有 CF l sin cot (4) 取杆 CD 为研究对象,由平衡条件有 4 2 2 N N f cos sin 0 (5) 2 2 N f mg sin cos 0 (6) 以及对C 点的力矩 4 1 cos sin 0 2 N l mgl (7) 解以上各式可得 4 1 tan 2 N mg (8) 3 3 1 sin 1 tan sin tan tan 2 2 cos 2 sin N mg (9) 1 3tan sin 1 tan sin 2 cos 2 sin f mg (10) 1 N mg 2 (11) 2 1 sin tan cos 2 N mg (12) 2 1 cos tan sin 2 f mg (13) CD 杆平衡的必要条件为 2 2 c f N (14) 由(12)、(13)、(14)式得 2 sin cos tan cos sin C C (15) AB 杆平衡的必要条件为 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 f≤44N (16) 由(10)、(11)(16)式得 tana sina (17) sin0 2simg≤4μ4-3tan8 cosa 因此,使系统平衡,a应满足的条件为(15)式和(17)式. 2.将题给的数据代入(15)式可得 a≤arctan0.385=21.1° (18) 将题给的数据代入(17)式,经数值计算可得 ≥19.5° (19 因此,a的取值范围为 19.5°≤a≤21.1° (20) 评分标准: 本题20分 第1问15分 (1)、(2)、(3)式共3分,(4)式1分,(5)、(6)、(7)式共3分,(9)、(10)式各1分,(12) 到(17)式各1分. 第2问5分 (18)式1分,(19)式3分,(20)式1分. 三、 参考解答: 解法一 1.设在时刻1,小球和圆筒的运动状态如图1所 示,小球位于P点,绳与圆筒的切点为T,P到T的 距离即绳的拉直部分的长度为1,圆筒的角速度为0, 小球的速度为).小球的速度可以分解成沿着绳子方向 的速度)1和垂直于绳子方向的速度V2两个分量.根据 图1 机械能守恒定律和角动量守恒定律有 M(Ra,广+m(Ra,广=M(Raj+m(+ (1) MR2@+mR2@o=MR'@+mRv +mlv? (2) 因为绳子不可伸长,)与切点T的速度相等,即 10
10 1 1 A f N (16) 由(10)、(11)、(16)式得 tan sin 2sin 4 3 tan sin cos A (17) 因此,使系统平衡, 应满足的条件为(15)式和(17)式. 2.将题给的数据代入(15)式可得 arctan 0.385 21.1 (18) 将题给的数据代入(17)式,经数值计算可得 19.5 (19) 因此, 的取值范围为 19.5 21.1 (20) 评分标准: 本题 20 分 第 1 问 15 分 (1)、(2)、(3)式共 3 分,(4)式 1 分,(5)、(6)、(7)式共 3 分,(9) 、(10) 式各 1 分,(12) 到(17)式各 1 分. 第 2 问 5 分 (18)式 1 分,(19)式 3 分,(20)式 1 分. 三、 参考解答: 解法一 1. 设在时刻t ,小球和圆筒的运动状态如图 1 所 示,小球位于 P 点,绳与圆筒的切点为T , P 到T 的 距离即绳的拉直部分的长度为l ,圆筒的角速度为 , 小球的速度为v .小球的速度可以分解成沿着绳子方向 的速度 1 v 和垂直于绳子方向的速度 2 v 两个分量.根据 机械能守恒定律和角动量守恒定律有 2 2 2 2 2 0 0 1 2 1 1 1 1 2 2 2 2 M R m R M R m v v (1) 2 2 2 MR mR MR mR ml 0 0 1 2 v v (2) 因为绳子不可伸长, 1 v 与切点T 的速度相等,即 2 v v 图 1 T O P 1 v 中国科学技术大学物理学院叶邦角整理