物理奥林匹克竞赛：全国物理奥林匹克竞赛第23届复赛试题（含参考答案）

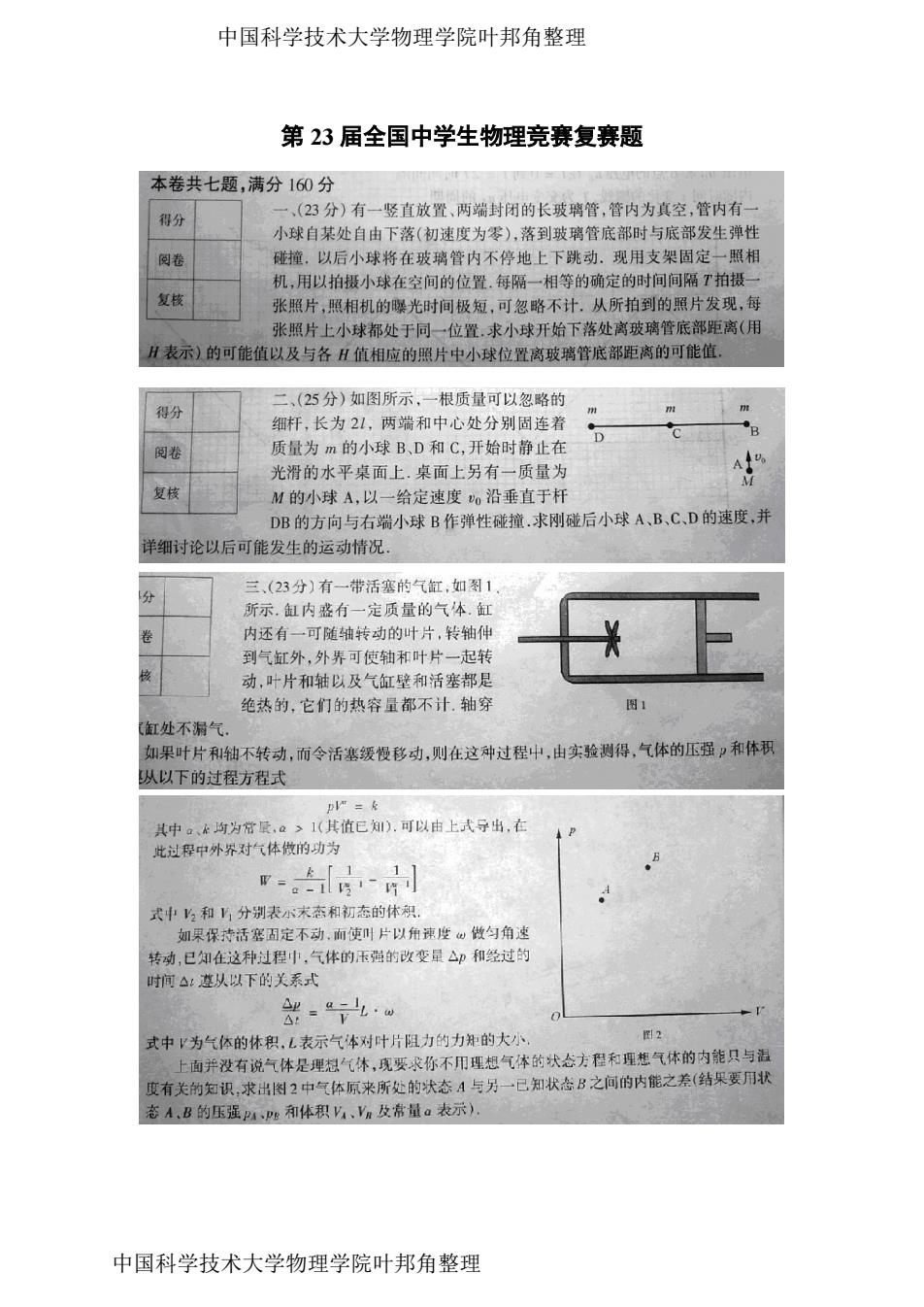
中国科学技术大学物理学院叶邦角整理 第23届全国中学生物理竞赛复赛题 本卷共七题，满分160分 得分 一、(23分)有一竖直放置、两端封闭的长玻璃管，管内为真空，管内有一 小球自某处自由下落（初速度为零），落到玻璃管底部时与底部发生弹性 阅卷 碰撞.以后小球将在玻璃管内不停地上下跳动.现用支架固定一照相 机，用以拍摄小球在空间的位置.每隔一相等的确定的时间间隔T拍摄一 复核 张照片，照相机的曝光时间极短，可忽略不计，从所拍到的照片发现，每 张照片上小球都处于同一位置求小球开始下落处离玻璃管底部距离（用 H表示)的可能值以及与各H值相应的照片中小球位置离玻璃管底部距离的可能值， 二、(25分)如图所示，一根质量可以忽略的 得分 细杆，长为21，两端和中心处分别固连着 B D 阅卷 质量为m的小球B、D和C,开始时静止在 光滑的水平桌面上.桌面上另有一质量为 复核 M的小球A,以一给定速度o沿垂直于杆 DB的方向与右端小球B作弹性碰撞.求刚碰后小球A、B、C、D的速度，并 详细时论以后可能发生的运动情况。 三、(23分)有一带活塞的气缸，如图1 分 所示.缸内盛有一定质量的气本.缸 卷 内还有一可随轴转动的叶片，转轴伸 到气缸外，外界可使轴和叶片一起转 动，叶片和轴以及气缸壁和活塞都是 绝热的，它们的热容量都不计轴穿 气缸处不漏气， 如果叶片和轴不转动，而令活塞缓慢移动，则在这种过程中，由实验测得，气体的压强？和体积 从以下的过程方程式 p"= 其中。、k均为常量，a>1(其值已知).可以由上式导出，在 此过程中外界对气体做的功为 -g 式中2和分别表小末态和初态的体积 如果保待活塞固定不动，而使叶片以角速度仙做匀角速 转动，已知在这种过程中，气体的，压猫的改变量△印和经过的 时间△：遵从以下的关系式 = 式中为气体的体积，L表示气体对叶片阻力的力知的大小。 图2 上面并没有说气体是理想气体，现要求你不用理想气体的状态方程和理想气体的内能只与温 度有关的知识，求出图2中气体原来所处的状态A与另一已知状态B之间的内能之差（结果要用状 态A,B的压强PA,Ps和体积V、Vn及常量a表示)， 中国科学技术大学物理学院叶邦角整理

第 23 届全国中学生物理竞赛复赛题 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

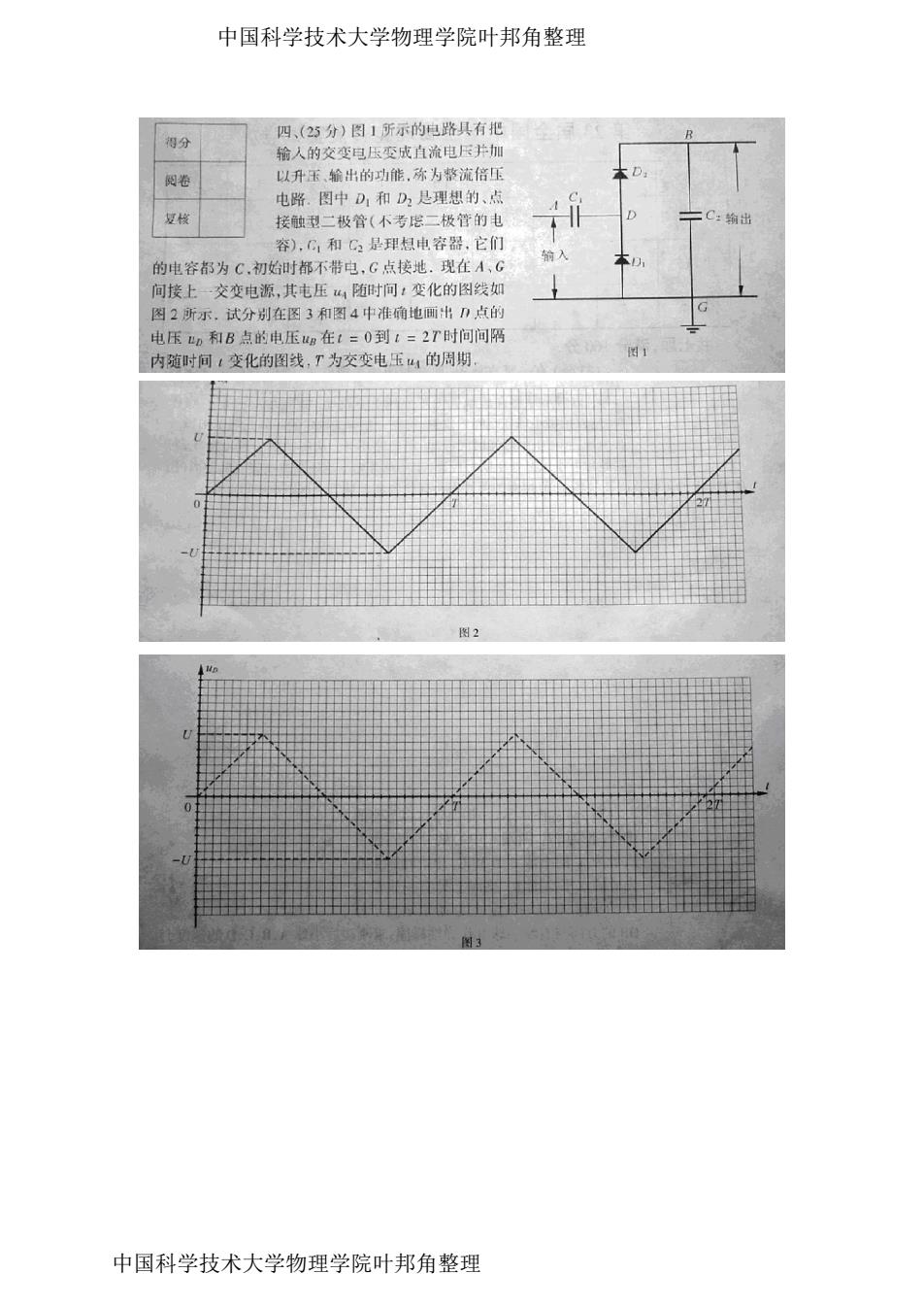
中国科学技术大学物理学院叶邦角整理 四、(25分)图1所示的包路具有把 得分 R 输人的交变旦压变成直流电压并加 阅卷 以升玉、输出的功能，称为整流倍压 本D 电路。图中D1和D是理想的、点 复核 接触型二极管（不考虑二极管的电 C:物出 容)，C,和C是理想电容器，它们 输入 的电容都为C,初始时都不带电，G点接地.现在A、G 本D 间接上一交变电源，其电压4随时间：变化的图线如 图2所示.试分别在图3和图4中准确地画出D点的 G 电压D和B点的电压ug在t=0到1=2T时间间隔 内随时间1变化的图线，T为交变电压，的周期 图1 图2 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

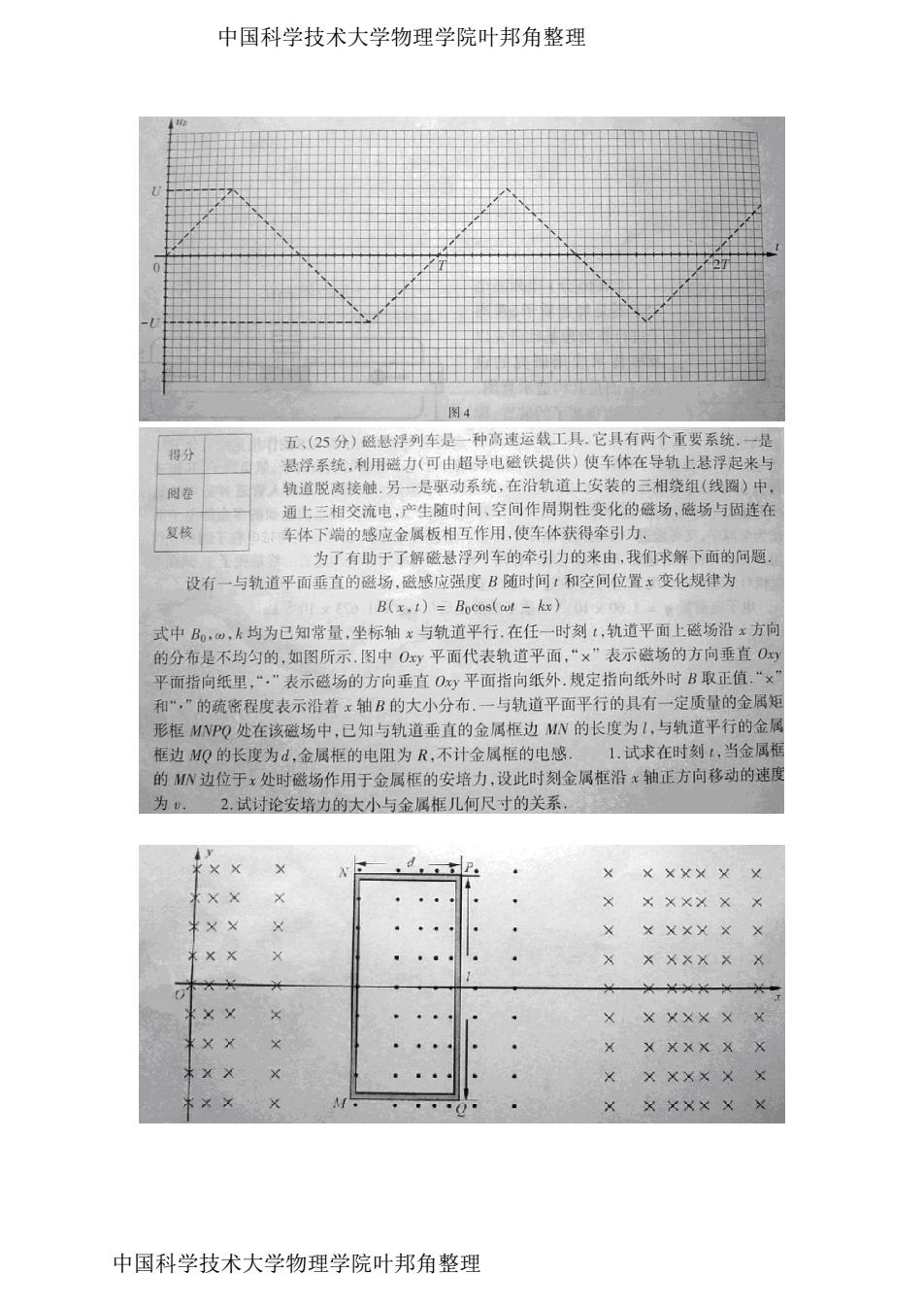
中国科学技术大学物理学院叶邦角整理 图4 五、(25分)磁悬浮列车是一种高速运载工具.它具有两个重要系统.一是 得分 悬浮系统，利用磁力（可由超导电磁铁提供）使车体在导轨上悬浮起来与 阅卷 轨道脱离接触.另一是驱动系统，在沿轨道上安装的三相绕组（线圈）中， 通上三相交流电，产生随时间、空间作周期性变化的磁场，磁场与固连在 复核 车体下端的感应金属板相互作用，使车体获得牵引力、 为了有助于了解磁悬浮列车的牵引力的来由，我们求解下面的问题。 设有一与轨道平面垂直的磁场，磁感应强度B随时间：和空间位置x变化规律为 B(x.t)=Bocos(at -kx) 式中B,m,k均为已知常量，坐标轴x与轨道平行.在任一时刻t,轨道平面上磁场沿x方向 的分布是不均匀的，如图所示，图中Oy平面代表轨道平面，“×”表示磁场的方向垂直O) 平面指向纸里，“.”表示磁场的方向垂直Oy平面指向纸外.规定指向纸外时B取正值.“× 和“，”的疏密程度表示沿着x轴B的大小分布.一与轨道平面平行的具有一定质量的金属矩 形框MNPQ处在该磁场中，已知与轨道垂直的金属框边MN的长度为L,与轨道平行的金属 框边MQ的长度为d,金属框的电阻为R,不计金属框的电感.1.试求在时刻1，当金属框 的M小边位于x处时磁场作用于金属框的安培力，设此时刻金属框沿x轴正方向移动的速度 为.2试讨论安培力的大小与金属框几何尺寸的关系。 ××××××× 米XX X XXX XX XX X XX×XX× XX XXX XX XX X××X×X× ×X×X××× 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 六、(23分)有一种称为直视 分光镜的光谱学仪器，所有光学 元件均放在一直长圆筒内，筒内 有：三个焦距分别为f2和方 的透镜L,L2和L,=f方> 观察屏P,它是一块带有刻度的 图1 玻璃片：由三块形状相同的等腰棱镜构成的分光元件（如图1所示），棱镜分别用折射率不同的玻璃 制成，两侧棱镜的质料相同，中间棱镜则与它们不同，棱镜底面与圆筒轴平行.圆筒的一端有一与圆 筒轴垂直的狭缝，它与圆简轴的交点为S,缝平行于棱镜的底面.当有狭缝的一端对准简外的光源 时，位于圆筒另一端的人眼可观察到屏上的光谱。 已知：当光源是钠光源时，它的黄色谱线（波长为589.3m,称为D线）位于圆筒轴与观察屏相 交处.制作棱镜所用的玻璃，一种为冕牌玻璃，它对钠D线的折射率D=1.5170:另一种为火石玻 璃，它对钠D线的折射率n6=1.7200. 1.试在图2中绘出圆筒内诸光学元件相对位置的示意图并说出各元件的作用. 2.试论证三块棱镜各应由何种玻璃制成并求出三棱镜的顶角α的数值 圆简轴 图2 得分 七、(16分)串列静电 加速器是加速质子、重离 阅卷 子进行核物理基础研究以 及核技术应用研究的设 复核 备，右图是其构造示意图。 S是产生负离子的装置，称 为离子源：中间部分N为充有氮气的管道，通 过高压装置H使其对地有5.00×10V的高压.现将氢气通入离子源S,S的作用是使氢分子变 为氢原子，并使氢原子粘附上一个电子，成为带有一个电子电量的氢负离子氢负离子（其初速 度为0)在静电场的作用下，形成高速运动的氢负离子束流，氢负离子束射入管道N后将与氮 气分子发生相互作用，这种作用可使大部分的氢负离子失去粘附在它们上面的多余的电子而 成为氢原子，又可能进一步剥离掉氢原子的电子使它成为质子.已知氮气与带电粒子的相互作 用不会改变粒子的速度.质子在电场的作用下由N飞向串列静电加速器的终端靶子T试在考 虑相对论效应的情况下，求质子到达T时的速度。. 电子电荷量g=1.60×10-19C,质子的静止质量m0=1.673×10-2”kg 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 第23届全国中学生物理竞赛复赛题参考解答及各题得分 一、参考解答： 解法一 小球沿竖直线上下运动时，其离开玻璃管底部的距离h随时间1变化的关系如图所示.设 照片拍摄到的小球位置用A表示，A离玻璃管底部的距离为4，小球开始下落处到玻璃管 底部的距离为H.小球可以在下落的过程中经过A点，也可在上升的过程中经过A点.现以 表示小球从最高点（即开始下落处）落到玻璃管底部所需 h 的时间（也就是从玻璃管底部反跳后上升到最高点所需的 时间)，表示小球从最高点下落至A点所需的时间（也 就是从A点上升至最高点所需的时间)，t2表示小球从A 点下落至玻璃管底部所需的时间（也就是从玻璃管底部反 跳后上升至A点所需的时间).显然，T1+t2=T.根据题 意，在时间间隔T的起始时刻和终了时刻小球都在A点.用表示时间间隔T内（包括起 始时刻和终了时刻)小球位于A点的次数(2).下面分两种情况进行讨论： 1,A点不正好在最高点或最低点. 当n为奇数时有 T=(n-1)x1+(n-1)x2=(n-1)z n=3,5,7,… (1 在(1)式中，根据题意x可取0<x<x中的任意值，而 T,=t-7 (2 当n为偶数时有 T=nr2+(n-2)x1=m1+(n-2)z2 n=2,4,6,… (3 由(3)式得 T1=T2 (4 由(1)、(3)、(4)式知，不论n是奇数还是偶数，都有 T=(n-1)x n=2,3,4,… (5 中国科学技术大学物理学院叶邦角整理

第 23 届全国中学生物理竞赛复赛题参考解答及各题得分 一、参考解答： 解法一 小球沿竖直线上下运动时，其离开玻璃管底部的距离h随时间 t 变化的关系如图所示．设 照片拍摄到的小球位置用 A 表示，A 离玻璃管底部的距离为 hA，小球开始下落处到玻璃管 底部的距离为 H.小球可以在下落的过程中经过 A 点，也可在上升的过程中经过 A 点.现以 表示小球从最高点（即开始下落处）落到玻璃管底部所需 的时间（也就是从玻璃管底部反跳后上升到最高点所需的 时间）， 1  表示小球从最高点下落至 A 点所需的时间（也 就是从 A 点上升至最高点所需的时间）， 2  表示小球从 A 点下落至玻璃管底部所需的时间（也就是从玻璃管底部反 跳后上升至 A 点所需的时间）.显然， 1 2      .根据题 意，在时间间隔的起始时刻和终了时刻小球都在 A 点．用 n 表示时间间隔 内（包括起 始时刻和终了时刻）小球位于 A 点的次数（n≥2）.下面分两种情况进行讨论： 1．A 点不正好在最高点或最低点． 当 n 为奇数时有       1 2 T n n n       1 1 1    n  3,5,7, （1） 在（1）式中，根据题意 1  可取 1 0     中的任意值，而 2 1      （2） 当 n 为偶数时有     2 1 1 2 T n n n n           2 2 n  2,4,6, （3） 由（3）式得 1 2    （4） 由（1）、（3）、（4）式知，不论 n 是奇数还是偶数，都有 T n    1 n  2,3,4, （5） t H O hA T h 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 因此可求得，开始下落处到玻璃管底部的距离的可能值为 n=2,3,4,… (6) 若用H,表示与n对应的H值，则与H,相应的A点到玻璃管底部的距离 1 h,=H,-28时 n=2,3,4,… (7) 当n为奇数时，T可取0<t1<x中的任意值，故有 0<h<H [a-(j n=3,5,7,·· (8) 可见与H相应的h,的可能值为0与H之间的任意值. 当n为偶数时，1= 二π，由(6)式、(7)式求得H的可能值 3 h=H 4 n=2,4,6,· (9) 2.若A点正好在最高点或最低点. 无论n是奇数还是偶数都有 T=2(n-1)x n=2,3,4,·… (10) n=2,3,4,.… (11) h=H。 n=2,3,4, (12) 或 ha=0 (13 解法二 因为照相机每经一时间间隔T拍摄一次时，小球都位于相片上同一位置，所以小球经 过该位置的时刻具有周期性，而且T和这个周期的比值应该是一整数.下面我们就研究小 中国科学技术大学物理学院叶邦角整理

因此可求得，开始下落处到玻璃管底部的距离的可能值为 2 1 1 2 2 2 1 n T H g g n           n  2,3,4, （6） 若用 Hn 表示与 n 对应的 H 值，则与 Hn 相应的 A 点到玻璃管底部的距离 2 1 1 2 A n h H g    n  2,3,4, （7） 当 n 为奇数时， 1  可取 1 0     中的任意值，故有 0 A n   h H 2 1 2 1 n T H g n               n=3,5,7,· · · （8） 可见与 Hn 相应的 A h 的可能值为 0 与 Hn 之间的任意值． 当 n 为偶数时， 1 1 2    ，由（6）式、（7）式求得 Hn 的可能值 3 4 A n h H  2 1 2 1 n T H g n               n=2,4,6,· · · （9） 2．若 A 点正好在最高点或最低点． 无论 n 是奇数还是偶数都有 T n   2 1   n=2,3,4,· · · （10）   2 1 1 2 2 2 2 1 n T H g g n             n=2,3,4,· · · （11） A n h H   2 1 2 2 1 n T H g n                     n=2,3,4,· · · （12） 或 0 A h  （13） 解法二 因为照相机每经一时间间隔 T 拍摄一次时，小球都位于相片上同一位置，所以小球经 过该位置的时刻具有周期性，而且 T 和这个周期的比值应该是一整数．下面我们就研究小 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 球通过某个位置的周期性， 设小球从最高点（开始下落处）落下至管底所需时间为x,从最高点下落至相片上小 球所在点(A点)所需时间为x,从A点下落至管底所需时间为2，则 t=T+T (1) (小球上升时通过相应路程段所需时间与下落时同一路程所需时间相同，也是πx和π，) 从小球在下落过程中经过A点时刻开始，小球经过的时间2x,后上升至A点，再经过 时间2x,后又落到A点，此过程所需总时间为2x+2x2=2π.以后小球将重复这样的运动.小 球周期性重复出现在A点的周期是多少？分两种情况讨论： (1).T1≠2，T和t2都不是小球在A点重复出现的周期，周期是2π. (2).1=t2,小球经过时间2x2=x回到A点，再经过时间2=T又回到A点，所 以小球重复出现在A点的周期为π. 下面就分别讨论各种情况中H的可能值和A点离管底的距离，的可能值.（如果从小 球在上升过程中经过A点的时刻开始计时，结果一样，只是x和τ，对调一下) 1.H的可能值 (1).较普遍的情况，T,≠t2·T与2π的比值应为一整数，T的可能值应符合下式 T =k, k=1,2,3,… (2) 2t 由自由落体公式可知，与此相应的H,的数值为 n.-) k=1,2,3, (3) (2).T,=t2·t的可能值应符合下式 T-k k'=1,2,3,… (4) 故H的可能值为 k'=1,2,3, 当k'为偶数时，即k'=2,4,6,…时，(5)式与(3)式完全相同.可见由(3)式求得的H的 中国科学技术大学物理学院叶邦角整理

球通过某个位置的周期性． 设小球从最高点（开始下落处）落下至管底所需时间为，从最高点下落至相片上小 球所在点（A 点）所需时间为 1  ，从 A 点下落至管底所需时间为 2  ，则 1 2      （1） （小球上升时通过相应路程段所需时间与下落时同一路程所需时间相同，也是、 1  和 2  ） 从小球在下落过程中经过 A 点时刻开始，小球经过的时间 2 2 后上升至 A 点，再经过 时间 1 2 后又落到 A 点，此过程所需总时间为 1 2 2 2 2      ．以后小球将重复这样的运动．小 球周期性重复出现在 A 点的周期是多少？ 分两种情况讨论： （1）． 1 2    ， 1  和 2  都不是小球在 A 点重复出现的周期，周期是2 ． （2）． 1 2    ，小球经过时间 2 2   回到 A 点，再经过时间 1 2   又回到 A 点，所 以小球重复出现在 A 点的周期为． 下面就分别讨论各种情况中 H 的可能值和 A 点离管底的距离 A h 的可能值．（如果从小 球在上升过程中经过 A 点的时刻开始计时，结果一样，只是 1  和 2  对调一下） 1．H 的可能值 （1）．较普遍的情况， 1 2    ．T 与 2 的比值应为一整数， 的可能值应符合下式 2 T k   ， k 1,2,3, （2） 由自由落体公式可知，与此相应的 Hk 的数值为 2 1 1 2 2 2 2 k T H g g k          k 1,2,3, （3） （2）． 1 2    ． 的可能值应符合下式 T k    k 1,2,3, （4） 故 Hk 的可能值为 2 1 1 2 2 2 k T H g g k           k 1,2,3, （5） 当 k为偶数时，即k  2,4,6,时，（5）式与（3）式完全相同．可见由（3）式求得的 H 的 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 可能值包含了1≠x2的全部情况和x=t2的一部分情况.当k'为奇数时，即k'=1,3,5,…时， 由(5)式得出的H的可能值为 k'=13,5,… (6) 它们不在(3)式之内，故(3)式和(6)式得出的H合在一起是H的全部的可能值 2.与各H值相应的h,的可能值 a.与H相应的h,的可能值 由于在求得(3)式时未限定A点的位置，故h,的数值可取0和H,之间的任意值，即 0≤ha≤H k=1,2,3,… (7) b.与H（k'为奇数)相应的h,的可能值 这些数值与A位于特定的位置，1==5 相对应，所以对于每一个H.对应的h。 是一个特定值，它们是 k'=1,3,5,… (8) 评分标准： 本题23分 二、参考解答： 1.求刚碰撞后小球A、B、C、D的速度 设刚碰撞后，小球A、B、C、D的速度分别为)A、、0c、D,并设它们的方向都 与？，的方向相同.由于小球C位于由B、C、D三球组成的系统的质心处，所以小球C的 速度也就是这系统的质心的速度.因碰撞前后四小球组成的质点组的动量守恒，故有 M'。=MoA+3mwc (1) 碰撞前后质点组的角动量守恒，有 0=mlvc +2mlop (2) 这里角动量的参考点设在与B球重合的空间固定点，且规定顺时针方向的角动量为正.因 为是弹性碰撞，碰撞前后质点组的动能相等，有 中国科学技术大学物理学院叶邦角整理

可能值包含了 1 2    的全部情况和 1 2    的一部分情况．当k为奇数时，即 k 1,3,5,时， 由（5）式得出的 H 的可能值为 2 1 2 k T H g k         k 1,3,5, （6） 它们不在（3）式之内，故（3）式和（6）式得出的 H 合在一起是 H 的全部的可能值． 2．与各 H 值相应的 A h 的可能值 a.与 Hk 相应的 A h 的可能值 由于在求得（3）式时未限定 A 点的位置，故 A h 的数值可取 0 和 Hk 之间的任意值，即 0 A k   h H 2 1 2 2 k T H g k              k 1,2,3, （7） b. 与 Hk （ k为奇数）相应的 A h 的可能值 这些数值与 A 位于特定的位置， 1 2 2      ，相对应，所以对于每一个 Hk 对应的 A h 是一个特定值，它们是 2 1 1 2 2 A k T h H g k          2 1 2 k T H g k                 k 1,3,5, （8） 评分标准： 本题 23 分 二、参考解答： 1． 求刚碰撞后小球 A、B、C、D 的速度 设刚碰撞后，小球 A、B、C、D 的速度分别为 A v 、 B v 、 C v 、 Dv ，并设它们的方向都 与 0 v 的方向相同．由于小球 C 位于由 B、C、D 三球组成的系统的质心处，所以小球 C 的 速度也就是这系统的质心的速度．因碰撞前后四小球组成的质点组的动量守恒， 故有 0 A C M M m v v v   3 （1） 碰撞前后质点组的角动量守恒，有 C D 0 2   ml ml v v （2） 这里角动量的参考点设在与 B 球重合的空间固定点，且规定顺时针方向的角动量为正．因 为是弹性碰撞，碰撞前后质点组的动能相等，有 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 Mo=)Mo+5moi+)mo2+)m哈 1 (3) 2 2 2 2 2 因为杆是刚性杆，小球B和D相对于小球C的速度大小必相等，方向应相反，所以有 0B-0c=0c-0n (4 解(1)、(2)(3)、(4)式，可得两个解 0e=0 (5) 和 4M 0e=5M+6m0 (6) 因为c也是刚碰撞后由B、C、D三小球组成的系统的质心的速度，根据质心运动定律，碰 撞后这系统的质心不可能静止不动，故(5)式不合理，应舍去.取(6)式时可解得刚碰撞 后A、B、D三球的速度 UA- 5M-6mvo (7 5M+6m 10M 0B 0 (8) 5M+6m 2M (9) 5M+6m 2.讨论碰撞后各小球的运动 碰撞后，由于B、C、D三小球组成的系统不受外力作用，其质心的速度不变，故小球 C将以(6)式的速度即vc= 4M 0沿)。方向作匀速运动.由(4)、(8)、(9)式可知， M+6m 碰撞后，B、D两小球将绕小球C作匀角速度转动，角速度的大小为 0=g-c=6M6 (10) 15M+6m1 方向为逆时针方向.由(7)式可知，碰后小球A的速度的大小和方向与M、m的大小有关， 下面就M、m取值不同而导致运动情形的不同进行讨论： ()⑦a=0,即碰撞后小球A停住，由(7)式可知发生这种运动的条件是 5M-6m=0 即 M=6 (11) m 5 (i)0但vA0和4M>5M-6m 中国科学技术大学物理学院叶邦角整理

2 2 2 2 2 0 A B C D 1 1 1 1 1 + 2 2 2 2 2 M M m m v v mv v v    （3） 因为杆是刚性杆，小球 B 和 D 相对于小球 C 的速度大小必相等，方向应相反，所以有 v v = v v B C C D   （4） 解（1）、（2）、（3）、（4）式，可得两个解 C v =0 （5） 和 C 0 4 5 6 M M m   v v （6） 因为 C v 也是刚碰撞后由 B、C、D 三小球组成的系统的质心的速度，根据质心运动定律，碰 撞后这系统的质心不可能静止不动，故（5）式不合理，应舍去．取（6）式时可解得刚碰撞 后 A、B、D 三球的速度 A 0 5 6 5 6 M m M m    v v （7） B 0 10 5 6 M M m   v v （8） D 0 2 5 6 M M m    v v （9） 2．讨论碰撞后各小球的运动 碰撞后，由于 B、C、D 三小球组成的系统不受外力作用，其质心的速度不变，故小球 C 将以（6）式的速度即 C 0 4 5 6 M M m   v v 沿 0 v 方向作匀速运动．由（4）、（8）、（9）式可知， 碰撞后，B、D 两小球将绕小球 C 作匀角速度转动，角速度的大小为 6 0 5 6 B M l M m      C v v v l （10） 方向为逆时针方向．由（7）式可知，碰后小球 A 的速度的大小和方向与 M、m 的大小有关， 下面就 M、m 取值不同而导致运动情形的不同进行讨论： （i） v =A 0 ，即碰撞后小球 A 停住，由（7）式可知发生这种运动的条件是 5 6 0 M m   即 6 5 M m  （11） （ii） Av A 0 但 v v A C  ，即碰撞后小球 A 沿 0 v 方向作匀速直线运动，但其速度小于小 球 C 的速度．由（7）式和（6）式，可知发生这种运动的条件是 5 6 0 M m   和   654 mMM 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 即 6 m)c,即碰撞后小球A仍沿V。方向运动，且其速度大于小球C的速度，发生 这种运动的条件是 M>6m (14) (V))A=c,即碰撞后小球A和小球C以相同的速度一起沿V。方向运动，发生这种 运动的条件是 M=6m (15) 在这种情形下，由于小球B、D绕小球C作圆周运动，当细杆转过180°时，小球D将 从小球A的后面与小球A相遇，而发生第二次碰撞，碰后小球A继续沿)，方向运动.根据 质心运动定理，C球的速度要减小，碰后再也不可能发生第三次碰撞.这两次碰撞的时间间 隔是 t=π-(5M+6m）ld (16) 6M℃00 从第一次碰撞到第二次碰撞，小球C走过的路程 2πl d=vt= (17) 3 3.求第二次碰撞后，小球A、B、C、D的速度 刚要发生第二次碰撞时，细杆已转过180°，这时，小球B的速度为Vo,小球D的速度为0B.在 第二次碰撞过程中，质点组的动量守恒，角动量守恒和能量守恒.设第二次刚碰撞后小球A、 B、C、D的速度分别为A、g、和，并假定它们的方向都与V的方向相同.注意到 (1)、(2)、(3)式可得 Mvo=MU+3muc (18) 0=mloc +2mloa (19) MR+mm 1 2 (20) 2 2 21 2 由杆的刚性条件有 -必=心-6 (21) (19)式的角动量参考点设在刚要发生第二次碰撞时与D球重合的空间点， 把(18)、(19)、(20)、(21)式与(1)、(2)、(3)、(4)式对比，可以看到它们除了 小球B和D互换之外是完全相同的.因此它们也有两个解 6=0 (22) 和 4M vc=5M+6m 0 (23) 中国科学技术大学物理学院叶邦角整理

即 6 6 5 m M m   （13） （iv） v v A C  ，即碰撞后小球 A 仍沿 0 v 方向运动，且其速度大于小球 C 的速度，发生 这种运动的条件是 M m  6 （14） （v） v v A C  ，即碰撞后小球 A 和小球 C 以相同的速度一起沿 0 v 方向运动，发生这种 运动的条件是 M m  6 （15） 在这种情形下，由于小球 B、D 绕小球 C 作圆周运动，当细杆转过180时，小球 D 将 从小球 A 的后面与小球 A 相遇，而发生第二次碰撞，碰后小球 A 继续沿 0 v 方向运动．根据 质心运动定理，C 球的速度要减小，碰后再也不可能发生第三次碰撞．这两次碰撞的时间间 隔是   0 0 π π π 5 6 6 M m l l t  M     v v （16） 从第一次碰撞到第二次碰撞，小球 C 走过的路程 C 2π 3 l d t   v （17） 3．求第二次碰撞后，小球 A、B、C、D 的速度 刚要发生第二次碰撞时，细杆已转过180，这时，小球B的速度为 D v ，小球D的速度为 B v ．在 第二次碰撞过程中，质点组的动量守恒，角动量守恒和能量守恒．设第二次刚碰撞后小球 A、 B、C、D 的速度分别为 A v 、 B v 、 C v 和 Dv ，并假定它们的方向都与 0 v 的方向相同．注意到 （1）、（2）、（3）式可得 0 A C M M m v v v     3 （18） C B 0 2   ml ml v v   （19） 2 2 2 2 2 0 A B C D 1 1 1 1 1 + 2 2 2 2 2 M M m m v v mv v v        （20） 由杆的刚性条件有 D C C B v v v v        （21） （19）式的角动量参考点设在刚要发生第二次碰撞时与 D 球重合的空间点． 把（18）、（19）、（20）、（21）式与（1）、（2）、（3）、（4）式对比，可以看到它们除了 小球 B 和 D 互换之外是完全相同的．因此它们也有两个解 C v  0 （22） 和 C 0 4 5 6 M M m    v v （23） 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理