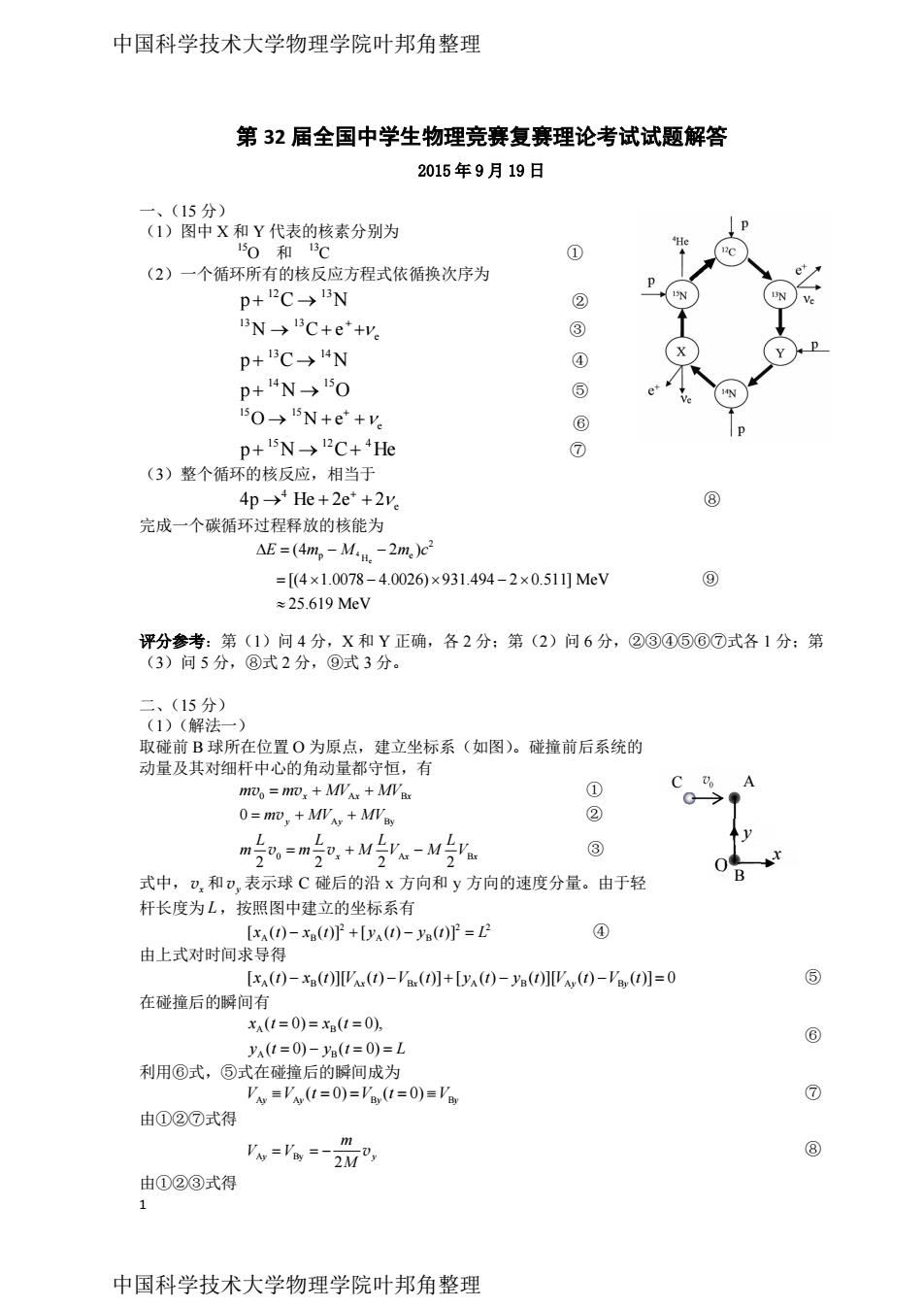
中国科学技术大学物理学院叶邦角整理 第32届全国中学生物理竞赛复赛理论考试试题解答 2015年9月19日 一、(15分) (1)图中X和Y代表的核素分别为 H 150和13C ① (2)一个循环所有的核反应方程式依循换次序为 p+2C→13N ② 13N→13C+e+y. ③ p+3C→I4N ⑦ p+4N→I5O ⑤ 5O→5N+e*+V. ⑥ p+l5N→12C+4He ⑦ (3)整个循环的核反应,相当于 4p→4He+2e*+2y ⑧ 完成一个碳循环过程释放的核能为 △E=(4mp-MH.-2m)e2 =[(4×1.0078-4.0026)×931.494-2×0.511]MeV ⑨ ≈25.619MeV 评分参考:第(1)问4分,X和Y正确,各2分:第(2)问6分,②③④⑤⑥⑦式各1分:第 (3)问5分,⑧式2分,⑨式3分。 二、(15分) (1)(解法一) 取碰前B球所在位置O为原点,建立坐标系(如图)。碰撞前后系统的 动量及其对细杆中心的角动量都守恒,有 m0o mo,MVAx MVB ① C A G→ 0=moy MVAy MVay ② m吃0=m子,+5-M5a L L ③ 2 式中,),和),表示球C碰后的沿x方向和y方向的速度分量。由于轻 杆长度为L,按照图中建立的坐标系有 [xA(1)-xB()+[yA()-yB(t)=L ④ 由上式对时间求导得 [xa(t)-x(t)]V(t)-'✉(t]+[yA(t)-y(t)]VA(t)-'(t]=0 ⑤ 在碰撞后的瞬间有 xA(1=0)=xB(1=0), y(t=0)-y(t=0)=L 利用⑥式,⑤式在碰撞后的瞬间成为 'A='A(t=0)='(t=0)=' ⑦ 由①②⑦式得 Vw='=-2M0y ⑧ 由①②③式得 y 中国科学技术大学物理学院叶邦角整理
1 第 32 届全国中学生物理竞赛复赛理论考试试题解答 2015 年 9 月 19 日 一、(15 分) (1)图中 X 和 Y 代表的核素分别为 15O 和 13C ① (2)一个循环所有的核反应方程式依循换次序为 12 13 p C N ② 13 13 N C e e ③ 13 14 p C N ④ 14 15 p N O ⑤ 15 15 O N e e ⑥ 15 12 4 p N C He ⑦ (3)整个循环的核反应,相当于 4 e 4p He 2e 2 ⑧ 完成一个碳循环过程释放的核能为 4 e 2 p e H (4 2 ) [(4 1.0078 4.0026) 931.494 2 0.511] MeV 25.619 MeV E m M m c ⑨ 评分参考:第(1)问 4 分,X 和 Y 正确,各 2 分;第(2)问 6 分,②③④⑤⑥⑦式各 1 分;第 (3)问 5 分,⑧式 2 分,⑨式 3 分。 二、(15 分) (1)(解法一) 取碰前 B 球所在位置 O 为原点,建立坐标系(如图)。碰撞前后系统的 动量及其对细杆中心的角动量都守恒,有 m m MV MV v v 0 A B x x x ① A By 0 m MV MV y y v ② 0 A B 2 2 2 2 x x x L L L L m m M V M V v v ③ 式中,vx 和 vy 表示球 C 碰后的沿 x 方向和 y 方向的速度分量。由于轻 杆长度为 L,按照图中建立的坐标系有 2 2 2 A B A B [ ( ) ( )] [ ( ) ( )] x t x t y t y t L ④ 由上式对时间求导得 A B A B A B A B [ ( ) ( )][ ( ) ( )] [ ( ) ( )][ ( ) ( )] 0 x x y y x t x t V t V t y t y t V t V t ⑤ 在碰撞后的瞬间有 A B A B ( 0) ( 0), ( 0) ( 0) x t x t y t y t L ⑥ 利用⑥式,⑤式在碰撞后的瞬间成为 A A B B ( 0) ( 0) V V t V t V y y y y ⑦ 由①②⑦式得 A By 2 y y m V V M v ⑧ 由①②③式得 x y O A B C 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 ="。-,) ⑨ M VBx=0 ⑩ 利用⑧⑨⑩式,碰撞后系统的动能为 m匠+时+号ME++Mg+g E、 1 2m@+)+5M+2) ① F2M(o。-0)2+2M+mmo 4M (解法二) 取碰前B球所在位置O为原点,建立坐标系(如图)。设碰撞后,小球C的运动速率为,细 杆中心的运动速度为'。,细杆绕中心转动的角速度为⊙。碰撞前后系统的动量及其对细杆中心的 角动量都守恒,有 mo=mv,+2MVc ① 0=mv,+2MVc ② 吃吃知+2w台片 ③ 式中,),和?,表示球C碰后的沿x方向和y方向的速度分量。由①②③式得 =%-) ④ =品0 ⑤ o=7a-) ⑥ 碰撞后系统的动能为 E=m++2wg+g+2x对oj ⑦ 利用④⑤⑥式,系统动能⑦式可表示成 E=m+a-旷+2画 ⑧ 4M (2)解法(一)的①式或者解法(二)的⑧式即为 E=1(M+m)m( +2W+m时 ② 可见,在条件 m 0x= M+m ③ 0,=0 下,碰后系统动能达到其最小值 E=1m6 2M+m 四 它是小球仅与球A做完全非弹性碰撞后系统所具有的动能。 评分参考:第(1)问10分,(解法一)①②③④⑤⑦⑧⑨⑩①式各1分:(解法二)①②式各1 分,③式2分,④⑤⑥各1分,⑦式2分,⑧式1分:第(2)问5分,②③式各2分,4式1 分。 中国科学技术大学物理学院叶邦角整理
2 A 0 ( ) x x m V M v v ⑨ VBx 0 ⑩ 利用⑧⑨⑩式,碰撞后系统的动能为 2 2 2 2 2 2 A Ay Bx By 2 2 2 2 A Ay 2 2 2 2 0 1 1 1 ( ) ( ) ( ) 2 2 2 1 1 ( ) ( 2 ) 2 2 1 1 2 ( ) 2 2 4 x y x x y x x x y E m M V V M V V m M V V m M m m m M M v v v v v v v v ⑪ (解法二) 取碰前 B 球所在位置 O 为原点,建立坐标系(如图)。设碰撞后,小球 C 的运动速率为v ,细 杆中心的运动速度为VC ,细杆绕中心转动的角速度为 。碰撞前后系统的动量及其对细杆中心的 角动量都守恒,有 m m MV v v 0 C x x 2 ① 0 2 m MV vy y C ② 0 2 2 2 2 2 x L L L L m m M v v ③ 式中,vx 和 vy 表示球 C 碰后的沿 x 方向和 y 方向的速度分量。由①②③式得 c 0 2 x x m V M v v ④ C 2 y y m V M v ⑤ 0 x m ML v v ⑥ 碰撞后系统的动能为 2 2 2 2 2 C C 1 1 1 ( ) (2 )( ) 2 2 2 2 2 x y x y L E m M V V M v v ⑦ 利用④⑤⑥式,系统动能⑦式可表示成 2 2 2 2 0 1 1 2 ( ) 2 2 4 x x y m M m E m m M M v v v v ⑧ (2)解法(一)的⑪式或者解法(二)的⑧式即为 2 2 2 2 0 0 1 ( ) 2 1 2 4 2 x y M m m m M m m E m M M m M M m v v v + v ⑫ 可见,在条件 0 , 0 x y m M m v v v ⑬ 下,碰后系统动能达到其最小值 2 2 0 1 2 m E M m v ⑭ 它是小球仅与球 A 做完全非弹性碰撞后系统所具有的动能。 评分参考:第(1)问 10 分,(解法一)①②③④⑤⑦⑧⑨⑩⑪式各 1 分;(解法二)①②式各 1 分,③式 2 分,④⑤⑥各 1 分,⑦式 2 分,⑧式 1 分;第(2)问 5 分,⑫⑬式各 2 分,⑭式 1 分。 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 三、(20分) (1)设圆环的质量为,它在碰撞过程中受到的地面对它的水平冲量为1,:碰撞后 圆环质心的速度大小为),)与竖直向上方向的夹角(按如图所示的顺时针方向计算) 为B,圆环的角速度为o。规定水平向右方向和顺时针方向分别为水平动量和角速度 的正方向。在水平方向,由动量定理有 mosin B-mo sin=I ① 由对质心的动量矩定理有 rm(ro)-rm(ro)=-rl, ② 按题意,圆环在弹起前刚好与地面无相对滑动,因而此时圆环上与地面的接触点的水 平速度为零,即 usin B-ro=0 ③ 由题意知 0-vcosβ ④ Vo cos0-0 联立①②③④式得 0=2V4k6cos20+(0a,+,sin9 ⑤ tanB=-1 2k (tan0+ ⑥ 。cosB 1 -(ro+vo sine) ⑦ (2)若圆环与地面碰后能竖直弹起,则其速度与竖直方向的夹角 B=0 将上式代入⑥式得,使圆环在与地面碰后能竖直弹起的条件为 sin0=-roo ⑧ Vo 在此条件下,在与地面刚刚碰后的瞬间有 0=0,0=-0kc0s0 ⑨ 即圆环做竖直上抛运动。圆环上升的最大高度为 hkcos ok'r) ⑩ 2g2g 2g (3)由于忽略空气阻力,圆环再次弹起后,角速度保持为。不变,质心做以初速度 为)的斜抛运动。圆环第二次落地点到首次落地点之间的水平距离s随0变化的函数关 系式为 s=U'sin28_kvocos -(v。sin0+ro)】 ① s取最大值时,θ的取值6满足 ② de _ke(cos20-r@osin0)=0 由得②式得 sina=-r%,±PG+8a网 ③ 40o 将③代入①式得 中国科学技术大学物理学院叶邦角整理
3 三、(20 分) (1)设圆环的质量为m ,它在碰撞过程中受到的地面对它的水平冲量为 t I ;碰撞后 圆环质心的速度大小为v,v与竖直向上方向的夹角(按如图所示的顺时针方向计算) 为 ,圆环的角速度为。规定水平向右方向和顺时针方向分别为水平动量和角速度 的正方向。在水平方向,由动量定理有 0 sin sin m m I t v v ① 由对质心的动量矩定理有 0 ( ) ( ) t rm r rm r rI ② 按题意,圆环在弹起前刚好与地面无相对滑动,因而此时圆环上与地面的接触点的水 平速度为零,即 vsin 0 r ③ 由题意知 0 0 cos cos 0 k v v ④ 联立①②③④式得 2 2 2 2 0 0 0 1 4 cos ( sin ) 2 v v v k r ⑤ 0 0 1 tan (tan ) 2 cos r k v ⑥ 0 0 1 ( sin ) 2 r r v ⑦ (2)若圆环与地面碰后能竖直弹起,则其速度与竖直方向的夹角 0 将上式代入⑥式得,使圆环在与地面碰后能竖直弹起的条件为 0 0 sin r v ⑧ 在此条件下,在与地面刚刚碰后的瞬间有 0, 0 v v k cosθ ⑨ 即圆环做竖直上抛运动。圆环上升的最大高度为 2 2 2 2 2 2 2 2 0 0 0 cos ( ) 2 2 2 k k r h g g g v vv ⑩ (3)由于忽略空气阻力,圆环再次弹起后,角速度保持为不变,质心做以初速度 为v的斜抛运动。圆环第二次落地点到首次落地点之间的水平距离 s随 变化的函数关 系式为 2 0 0 0 cossin 2 ( sin ) k s r g g vv v ⑪ s 取最大值时, 的取值 满足 0 0 0 ( cos2 sin ) 0 kds r d g v v ⑫ 由得⑫式得 2 2 2 0 0 0 0 8 sin 4 r r v v ⑬ 将⑬代入⑪式得 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 ++3rm)ysv-2re (ra) ④ 16g k(yraj+803-3r@)8v-2r@o(roo+yrog +8v3) ⑤ 16g 式中s和s,分别对应于③式右端根号前取正和负号的情形。由以上两式可知,s的最 大值为 k(rai +8vi +3rleoly8vi-2rleol(rleol-rai +8vi) ⑥ 16g 又因为 -1rao ⑩ 评分参考:第(1)问9分,①②式各2分,③④⑤⑥⑦式各1分:第(2)问4分,⑧⑨式各1 分,⑩式2分;第(3)问7分,①②③④⑤6⑦式各1分。 四、(25分) (1)解法(一) 按照题给坐标系,设待测点P的位置为(xp,0,a),飞机在 t=0时所在点K的位置为(0,h,0)。在时刻4,飞机所在位置A 点的坐标为(x1=x,h,0),,机载雷达此时发出一光信号;该信 号到达P点,经反射后,于时刻返回至飞机的机载雷达被接 受,此时飞机的机载雷达的位置为(x2=x,h,O),如图所示。 由于光速不变,飞机做匀速直线运动,有 √R+(x-x)2+√R+(x2-x)2=C(2-4) ① x2-x1=(52-4) ② 式中R=√?+a2。现设在时刻,飞机所在位置A点的坐标 为(x,h,0),机载雷达此时发出另一光信号:该信号到达P点, 经反射后,于时刻返回至飞机的机载雷达被接受,此时飞机 图(a) 的机载雷达的位置为(x5,h,0)。同理有 R+(xi-xp)+R+x-xp)=c(5-f) ③ x-x=(5-) ④ x-x=(-4) ⑤ x-x2=(6-42) 由①②式和v<c得 4-4=[底+%-+E+(偶-+-矿] -[®+G-F+E+(偶-护+2飞-名x-)+G-x] ⑥ =【民+6-o+E+6-广+26-4-,+6- 2WR+(出-x x1-xp 0 (4-4) √R6+(x-xp)2c 中国科学技术大学物理学院叶邦角整理
4 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 1 ( 8 3 ) 8 2 ( 8 ) 16 k r r r r r s g v v v ⑭ 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 2 ( 8 3 ) 8 2 ( 8 ) 16 k r r r r r s g v v v ⑮ 式中 1 s 和 2 s 分别对应于⑬式右端根号前取正和负号的情形。由以上两式可知, s 的最 大值为 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 max ( 8 3 ) 8 2 ( 8 ) 16 k r r r r r s g v v v ⑯ 又因为 1 sin 1 由上式得,当 s 取最大值时,r 、 v0 和0 应满足 0 0 v r ⑰ 评分参考:第(1)问 9 分,①②式各 2 分,③④⑤⑥⑦式各 1 分;第(2)问 4 分,⑧⑨式各 1 分,⑩式 2 分;第(3)问 7 分,⑪⑫⑬⑭⑮⑯⑰式各 1 分。 四、(25 分) (1)解法(一) 按照题给坐标系,设待测点 P 的位置为 P ( ,0, ) x a ,飞机在 t 0时所在点 K 的位置为(0, ,0) h 。在时刻 1 t ,飞机所在位置 A 点的坐标为 1 A ( , ,0) x x h ,机载雷达此时发出一光信号;该信 号到达 P 点,经反射后,于时刻 2t 返回至飞机的机载雷达被接 受,此时飞机的机载雷达的位置为 2 A ( , ,0) x x h ,如图所示。 由于光速不变,飞机做匀速直线运动,有 2 2 2 2 0 1 P 0 2 P 2 1 R x x R x x c t t ( ) ( ) ( ) ① 2 1 2 1 x x t t v( ) ② 式中 2 2 R h a 0 。现设在时刻 1 t,飞机所在位置 A 点的坐标 为 1 ( , ,0) x h ,机载雷达此时发出另一光信号;该信号到达 P 点, 经反射后,于时刻 2t 返回至飞机的机载雷达被接受,此时飞机 的机载雷达的位置为 2 ( , ,0) x h 。同理有 2 2 2 2 0 1 P 0 2 P 2 1 R x x R x x c t t ( ) ( ) ( ) ③ 2 1 2 1 x x t t v( ) ④ 1 1 1 1 x x t t v( ) ⑤ 2 2 2 2 x x t t v( ) 由①②式和v c 得 2 2 2 2 2 1 0 1 P 0 1 P 2 1 2 2 2 2 2 0 1 P 0 1 P 2 1 1 P 2 1 2 2 2 2 2 2 0 1 P 0 1 P 2 1 1 P 2 1 2 2 0 1 P 1 P 2 2 0 1 P 1 ( ) ( ) 1 ( ) ( ) 2( )( ) ( ) 1 ( ) ( ) 2 ( )( ) ( ) 2 ( ) ( ( ) t t R x x R x x x x c R x x R x x x x x x x x c R x x R x x t t x x t t c R x x x x t c c R x x v v v 2 1 t ) ⑥ 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 上式右端已略去了(o/c)级的高阶项。由⑥式解得 2VR+(x,-x了 t2-t1 c 1-0 R+(x-xp) 2VR+(x-xn月 ⑦ X1-xp c cRi+(x-xp)2 2Ro+(x-xp) 20 C (x-xp) 同理,由③④式和v<c得 6-42+- 20 +c2(x-x) ⑧ 由⑦⑧式得 G-5)-G-0风+G-x-风+(G-x,)+2x-x) ⑨ 利用⑤式,⑨式成为 (-4)-(G-4) 2+-+4--+6-)+2g-0 ⑩ 2x-x)=”(g-4) R+(x1-xp)2c 上式右端已略去了(o/c)2级的高阶项。令 -4=T。 ① 式中,T。为机载雷达在发射的光信号的周期,则 5-12=T @ 是机载雷达接受到相应的光信号的周期。①式可写成 T-T=1 2x-x)”五。 3 Ri+(xx)c 或 f6三f-f6=- 式中x已用x替代,而 1 1 是相应的光信号的频率,是接收到的回波信号的频率与发出信号的频率之差(频移)。①式也 可写为 6=f-6=-226cosa ④ c 式中 cosa=- XA一Xp R+(xA-x)月 即α为从机载雷达射出的光线与飞机航线之间的夹角。 解法(二) 取航线KA和直线BC所构成的平面为新的坐标平面。K为坐标原点,航线KA为x轴,从K 指向BC与Z轴交点的直线为y轴:在时刻1,飞机所在位置A点的坐标为(:=xA,O):目标点P 的位置(xp,R)在这个坐标系里是固定的。 中国科学技术大学物理学院叶邦角整理
5 上式右端已略去了 2 ( / ) v c 级的高阶项。由⑥式解得 2 2 0 1 P 2 1 1 2 2 0 1 P 2 2 0 1 P 1 P 2 2 0 1 P 2 2 0 1 P 2 1 P 2 ( ) 1 1 ( ) 2 ( ) 1 ( ) 2 ( ) 2 ( ) R x x t t c x c R x x R x x x x c c R x x R x x x x c c v v v ⑦ 同理,由③④式和v c 得 2 2 0 1 P 2 1 1 P 2 2 ( ) 2 ( ) R x x t t x x c c v ⑧ 由⑦⑧式得 2 2 2 2 2 2 1 1 0 1 P 0 1 P 1 1 2 2 2 ( ) ( ) ( ) ( ) ( ) t t t t R x x R x x x x c c v ⑨ 利用⑤式,⑨式成为 2 2 1 1 2 2 2 2 2 0 1 P 1 1 0 1 P 1 1 2 1 P 1 1 2 2 0 1 P ( ) ( ) 2 2 [ ( )] ( ) ( ) 2( ) ( ) ( ) t t t t R x x t t R x x t t c c x x t t R x x c v v v ⑩ 上式右端已略去了 2 ( / ) v c 级的高阶项。令 1 1 0 t t T ⑪ 式中,T0 为机载雷达在发射的光信号的周期,则 2 2 t t T ⑫ 是机载雷达接受到相应的光信号的周期。⑪式可写成 A P 0 0 2 2 0 A P 2( ) ( ) x x T T T R x x c v ⑬ 或 A P D 0 0 2 2 0 A P 2( ) ( ) x x f f f f R x x c v ⑭ 式中 1 x 已用 Ax 替代,而 0 0 1 1 f f , T T 是相应的光信号的频率, Df 是接收到的回波信号的频率与发出信号的频率之差(频移)。⑭式也 可写为 D 0 0 f f f f 2 cos c v ⑭ 式中 A P 2 2 0 A P cos ( ) x x R x x 即 为从机载雷达射出的光线与飞机航线之间的夹角。 解法(二) 取航线 KA 和直线 BC 所构成的平面为新的坐标平面。K 为坐标原点,航线 KA 为 x 轴,从 K 指向 BC 与 Z 轴交点的直线为 y 轴;在时刻 1 t ,飞机所在位置 A 点的坐标为 1 A ( ,0) x x ;目标点 P 的位置 P 0 ( , ) x R 在这个坐标系里是固定的。 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 设机载雷达于时刻1发出的发射信号的相位为 D(t)=0,1+p 式中o,和p分别是相应的角频率和初相位。机载雷达于时刻1在A'点(x,=xa(),0)接收到的经P 反射的信号是机载雷达于时刻1-π在A点(x=x(-t),0)发出的,其相位为 (4)=(4-t)+p ① 式中x为信号往返过程所需的时间,它满足 VR+(:-x,了+VR+(x-x=c红 ② X2-X1=0m ③ 经过时间间隔△t,同理有 D(4+△)=(4+△1-t)+p ④ VR+(xi-xp)++(x-xp)=cr' ⑤ X2-X=UT' ⑥ 另外,由于同样的原因(飞机作匀速直线运动),还有 X-x=0△M ⑦ x-x2=0△1 设机载雷达收到的信号的圆频率为。,则应有 D'(4+△)-D(4)=△1 ⑧ 由②③式和v<c得 -[+(偶+瓜店+-+西] -民+6-了+E+(-广+20--+6-] ⑨ =[+6-+E+-广+2r(-)+07 2+3- -p卫, Ro+(x-xp)c 上式右端已略去了(o/c级的高阶项。由⑨式解得 2+偶-羽 1、0 c√R+(x-xp) 2R+(x-xp) ⑩ 1+ c cR+(x-xp) 2VR+(x-x)22 c c(-p) 同理,由⑤⑥式和v<c得 2医6+- ① 由①④⑧式得 0△1=(△1-t)-(-t) @ 将 o=2nf ③ 代入②式,利用⑦⑩①式,在△1很小的情形下,略去△1的高阶项,得 fb三f-f6=- 2(xA-Xp)卫 Ro+(xA-xp)c 6 中国科学技术大学物理学院叶邦角整理
6 设机载雷达于时刻t发出的发射信号的相位为 0 t t 式中 0和 分别是相应的角频率和初相位。机载雷达于时刻 1 t 在A点 2 A 1 ( ( ),0) x x t 接收到的经 P 反射的信号是机载雷达于时刻 1 t 在A 点 1 A 1 ( ( ),0) x x t 发出的,其相位为 t t 1 0 1 ① 式中 为信号往返过程所需的时间,它满足 2 2 2 2 0 1 P 0 2 P R x x R x x c ( ) ( ) ② 2 1 x x v ③ 经过时间间隔t ,同理有 t t t t 1 0 1 ④ 2 2 2 2 0 1 P 0 2 P R x x R x x c ( ) ( ) ⑤ 2 1 x x v ⑥ 另外,由于同样的原因(飞机作匀速直线运动),还有 1 1 x x t v ⑦ 2 2 x x t v 设机载雷达收到的信号的圆频率为 ,则应有 t t t t 1 1 ⑧ 由②③式和v c 得 2 2 2 2 0 1 P 0 1 P 2 1 2 2 2 2 2 0 1 P 0 1 P 2 1 1 P 2 1 2 2 2 2 2 2 0 1 P 0 1 P 1 P 2 2 0 1 P 1 P 2 2 0 1 P 1 ( ) ( ) 1 ( ) ( ) 2( )( ) ( ) 1 ( ) ( ) 2 ( ) 2 ( ) ( ) R x x R x x x x c R x x R x x x x x x x x c R x x R x x x x c R x x x x c c R x x v v v ⑨ 上式右端已略去了 2 ( / ) v c 级的高阶项。由⑨式解得 2 2 0 1 P 1 2 2 0 1 P 2 2 0 1 P 1 P 2 2 0 1 P 2 2 0 1 P 2 1 P 2 ( ) 1 1 ( ) 2 ( ) 1 ( ) 2 ( ) 2 ( ) R x x c x c R x x R x x x x c c R x x R x x x x c c v v v ⑩ 同理,由⑤⑥式和v c 得 2 2 0 1 P 2 1 P 2 ( ) 2 ( ) R x x x x c c v ⑪ 由①④⑧式得 0 0 t t ( ) ( ) ⑫ 将 2πf ⑬ 代入⑫式,利用⑦⑩⑪式,在t 很小的情形下,略去t 的高阶项,得 A P D 0 0 2 2 0 A P 2( ) ( ) x x f f f f R x x c v ⑭ 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 或 )=f-6=-226c0sa ④ 式中 cosa=- XA-Xp R+(xA-xp) 即α为从机载雷达射出的光线与飞机航线之间的夹角。 (2)由于机载雷达天线发射的无线电波束面的张角的限制(见图(b),有 L,/2 5≤as+ L,/2 ⑤ 2√R+(L,122VR+(,12 频移。分别为正、零或负的条件是: 当a0: L/2 当9=π/2(x=x)时,即机载雷达发射信号时正好位于P 点到航线的垂足处,频移 f6=0 ⑥ 当0>π/2(x>x)时,频移fDL,有0 中国科学技术大学物理学院叶邦角整理
7 或 D 0 0 f f f f 2 cos c v ⑭ 式中 A P 2 2 0 A P cos ( ) x x R x x 即 为从机载雷达射出的光线与飞机航线之间的夹角。 (2)由于机载雷达天线发射的无线电波束面的张角的限制(见图(b)),有 2 2 2 2 0 0 π π / 2 / 2 2 2 ( / 2) ( / 2) s s s s L L R L R L ⑮ 频移 Df 分别为正、零或负的条件是: 当 π / 2 ( A P x x )时,频移 fD 0; 当 π / 2 ( A P x x )时,即机载雷达发射信号时正好位于 P 点到航线的垂足处,频移 fD 0 ⑯ 当 π / 2 ( A P x x )时,频移 0 Df 。 当 2 2 0 π / 2 / 2 ( / 2) L R L s s ( A P x x L s /2 )时,即机载 雷达发射信号时正好位于 A P ( /2, ,0) s x x L h 处,正的频移最大 D1 0 2 2 0 ( / 2) s s L f f R L c v ⑰ 当 2 2 0 π / 2 / 2 ( / 2) L R L s s ( A P x x L s /2)时,即机载雷 达发射信号时正好位于 A P ( /2, ,0) s x x L h 处,负的频移的绝对值最大 D2 0 2 2 0 ( / 2) s s L f f R L c v ⑱ (3)在飞机持续发射的无线电波束前沿 BC 全部通过目标 P 点过程中,多普勒频移的带宽为 1 2 0 0 2 2 0 2 4 sin ( / 2) 2 s D D D s L f f f f f R L c c v v ⑲ 由于 R L 0 s ,有 1,故 sin 2 2 将上式代入到⑲式得 0 2 Df f c v ⑳ 评分参考:第(1)问 16 分, (解法一) ①式 2 分,②式 1 分,③式 2 分,④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭式各 1 分; (解法二) ①式 1 分,②式 2 分,③④式各 1 分,⑤式 2 分,⑥⑦⑧⑨⑩⑪⑫⑬⑭式各 1 分; 第(2)问 6 分,⑮式 2 分,频移 Df 分别为正、零或负的条件正确(包括⑯式)给 2 分,⑰⑱ 式各 1 分; 第(3)问 3 分, ⑲式 2 分,⑳式 1 分。 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理
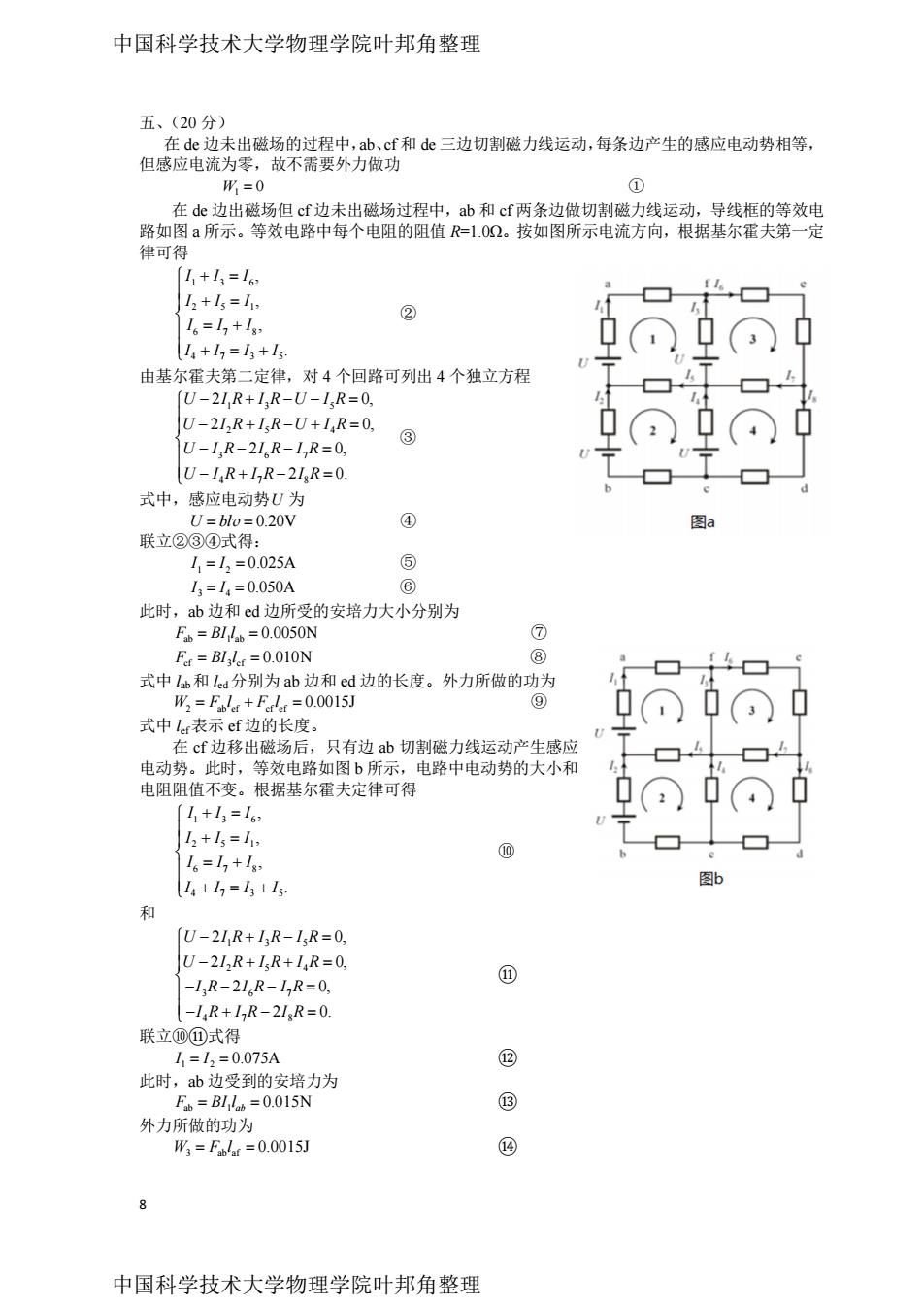
中国科学技术大学物理学院叶邦角整理 五、(20分) 在de边未出磁场的过程中,b、cf和de三边切割磁力线运动,每条边产生的感应电动势相等, 但感应电流为零,故不需要外力做功 W=0 ① 在de边出磁场但cf边未出磁场过程中,ab和cf两条边做切割磁力线运动,导线框的等效电 路如图a所示。等效电路中每个电阻的阻值R=1.02。按如图所示电流方向,根据基尔霍夫第一定 律可得 I+13=16, 12+13=1, ③ 16=1+1g, I4+1,=13+13 由基尔霍夫第二定律,对4个回路可列出4个独立方程 (U-21R+1R-U-IR=0. U-21,R+IR-U+IR=0, U-IR-2IR-1R=0, ③ U-I R+1R-2IgR=0. 式中,感应电动势U为 U=blo=0.20V ④ 图a 联立②③④式得: I1=13=0.025A ⑤ I3=I4=0.050A ⑥ 此时,ab边和cd边所受的安培力大小分别为 F=BI1b=0.0050N ① Fr =BI ler =0.010N ⑧ 式中lab和led分别为ab边和ed边的长度。外力所做的功为 W2=Fipler Frler =0.0015J ⑨ 式中ler表示ef边的长度。 在cf边移出磁场后,只有边ab切割磁力线运动产生感应 电动势。此时,等效电路如图b所示,电路中电动势的大小和 电阻阻值不变。根据基尔霍夫定律可得 1+13=16 12+1=11 ⑩ 16=17+1g, I4+17=13+I5 图b 和 [U-2I,R+I3R-1R=0, U-21,R+IR+IR=0, ① -I,R-2IR-I,R=0, -1,R+12R-2IR=0. 联立⑩①式得 11=12=0.075A ② 此时,ab边受到的安培力为 Fip=BI lo =0.015N ⑧ 外力所做的功为 W3=Fla=0.0015J ④ 中国科学技术大学物理学院叶邦角整理
8 五、(20 分) 在 de 边未出磁场的过程中,ab、cf 和 de 三边切割磁力线运动,每条边产生的感应电动势相等, 但感应电流为零,故不需要外力做功 W1 0 ① 在 de 边出磁场但 cf 边未出磁场过程中,ab 和 cf 两条边做切割磁力线运动,导线框的等效电 路如图 a 所示。等效电路中每个电阻的阻值 R=1.0Ω。按如图所示电流方向,根据基尔霍夫第一定 律可得 1 3 6 2 5 1 6 7 8 4 7 3 5 , , , . I I I I I I I I I I I I I ② 由基尔霍夫第二定律,对 4 个回路可列出 4 个独立方程 1 3 5 2 5 4 3 6 7 4 7 8 2 0, 2 0, 2 0, 2 0. U I R I R U I R U I R I R U I R U I R I R I R U I R I R I R ③ 式中,感应电动势U 为 U bl v 0.20V ④ 联立②③④式得: I I 1 2 0.025A ⑤ I I 3 4 0.050A ⑥ 此时,ab 边和 ed 边所受的安培力大小分别为 F BI l ab 1 ab 0.0050N ⑦ F BI l cf 3 cf 0.010N ⑧ 式中 lab和 led分别为 ab 边和 ed 边的长度。外力所做的功为 W F l F l 2 ab ef cf ef 0.0015J ⑨ 式中 lef表示 ef 边的长度。 在 cf 边移出磁场后,只有边 ab 切割磁力线运动产生感应 电动势。此时,等效电路如图 b 所示,电路中电动势的大小和 电阻阻值不变。根据基尔霍夫定律可得 1 3 6 2 5 1 6 7 8 4 7 3 5 , , , . I I I I I I I I I I I I I ⑩ 和 1 3 5 2 5 4 3 6 7 4 7 8 2 0, 2 0, 2 0, 2 0. U I R I R I R U I R I R I R I R I R I R I R I R I R ⑪ 联立⑩⑪式得 I I 1 2 0.075A ⑫ 此时,ab 边受到的安培力为 F BI l ab 1 ab 0.015N ⑬ 外力所做的功为 W F l 3 ab af 0.0015J ⑭ 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 整个过程中外力做的功为 W=W,+W2+W=0.0030J ⑤ 评分参考:①式1分,②③④式各2分,⑤⑥⑦⑧⑨式各1分,⑩①式各2分,②③④⑤式各 1分。 六、(23分) (1)设t时刻导线框平面与长直导线和转轴组成平面之间的夹角为0的值为0=o1,如图a所示 (俯视图),导线框旋转过程中只有左、右两边(图中分别用A、B表示)切割磁力线产生感应电 动势。A、B两条边的速度大小相等, 0=0a ① A、B处对应的磁感应强度大小分别为 B =Mol ② 2πr B=1 ③ -2π52 其中,,为真空磁导率,r1、n分别为A和B到长直导线 的垂直距离。A、B两边对应的感应电动势分别为 图a E,=B2 avsin,名=oc4sin名 πr ④ E2 B,2avsin x2= oauol sin π3 式中受么、2方分别为A、B的速度方向与小、n的夹角。 根据几何关系得 %=0+a ⑤ X2=0-B 其中a、B分别为”、2与x方向的夹角。⑤式代入④式得导线框中的感应电动势为 E=E+E=sin(+a)sin(0-B) ⑥ π 根据几何关系及三角形余弦定理得a、B、n1、n与a、b、0之间的关系为 b-acose cosa= ⑦ sina=asin cos B= b+acosθ ⑧ sin B=asin n r=a2+b2-2abcos0 ⑨ =a+b2+2abcos0 将⑦⑧⑨式代入⑥式得导线框的感应电动势为 9 中国科学技术大学物理学院叶邦角整理
9 整个过程中外力做的功为 W W W W 1 2 3 0.0030J ⑮ 评分参考:①式 1 分,②③④式各 2 分,⑤⑥⑦⑧⑨式各 1 分,⑩⑪式各 2 分,⑫⑬⑭⑮式各 1 分。 六、(23 分) (1)设 t 时刻导线框平面与长直导线和转轴组成平面之间的夹角为 θ 的值为 = t ,如图 a 所示 (俯视图),导线框旋转过程中只有左、右两边(图中分别用 A、B 表示)切割磁力线产生感应电 动势。A、B 两条边的速度大小相等, v a ① A、B 处对应的磁感应强度大小分别为 0 1 1 2 I B r ② 0 2 2 2 I B r ③ 其中,0 为真空磁导率,r1、r2分别为 A 和 B 到长直导线 的垂直距离。A、B 两边对应的感应电动势分别为 2 0 1 1 1 1 2 0 2 2 2 2 2 2 sin sin 2 sin sin a I E B a r a I E B a r 1 v v ④ 式中 1 π 2 、 2 π 2 分别为 A、B 的速度方向与 r1、r2的夹角。 根据几何关系得 1 2 ⑤ 其中 α、β 分别为 r1、r2与 x 方向的夹角。⑤式代入④式得导线框中的感应电动势为 2 0 1 1 2 1 2 a I sin( ) sin( ) E E E r r ⑥ 根据几何关系及三角形余弦定理得 α、β、r1、r2与 a、b、θ 之间的关系为 1 1 cos cos sin sin b a r a r ⑦ 2 2 cos cos sin sin b a r a r ⑧ 2 2 2 1 2 2 2 2 2 cos 2 cos r a b ab r a b ab ⑨ 将⑦⑧⑨式代入⑥式得导线框的感应电动势为 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理

中国科学技术大学物理学院叶邦角整理 E=wa't lbsin 1 1 a2+b2-2abcos0 a'+b2+2abcose ⑩ a'bulosin a 1 1 π a2+b2-2abcosot a2+b2+2abcosot (2)(解法一) 导线框在电流I的磁场中旋转,受到安培力相对于轴的合力矩M。的作用,要使导线框保持角 速度为0的匀速旋转,所加的外力矩M必须满足 M+M。=0 ① 正方形导线框上、下两边所受安培力的方向与转轴平行, B 力矩为零,只有导线框左、右两边(分别用A、B表示) 受到的安培力F和F对合力矩有贡献,如图b所示(俯 视图)。由②③式和安培力公式得F和F的大小为 -0+B F=2aiB,=Lali ② a πr d F3=2aiB,=Lali ⑧ 元 -0- π3 式中ⅰ为导线框中的感应电流。由欧姆定律有 图b E wa'u Ibsinot 1 1 RπR a2+b2-2abcosot ④ a2+b2+2abcosot 安培力的合力矩为 Mo=Fid+F2dz -Faco-0-a)+Fjacod+) Fasin(0+a)+Fasin(0-B) ⑤ lsin(0+a)sin(0-B) π 其中,d和山分别为F和F与转轴之间的垂直距离,无-0-a和?-日+B分别为d和d山2与A、 B连线之间的夹角。 将⑦⑧⑨④式代入⑤式得需要加的外力矩为 M=-M=Ha'libsin ot 1 1 a2+b2-2abcosot'a2+b2+2abcosot =-ta'b losin'ot 1 12 π2R a2+b2-2abcosot ⑥ a2+b2+2abcosot Auia'b'P (a2+b2)sinot π2R (a2+b2)-4a"b2 cos'@t (2)(解法二) 导线框在电流I的磁场中旋转,受到安培力相对于轴的合力矩M。的作用,要使导线框保持角 速度为o的匀速旋转,所加的外力矩M必须满足 M+M。=0 ① 此时,安培力的合力矩的功率Po应与导线框中感应电流的功率P:相等,即 P=P ② 式中 £=E-oa61sim2om 1 1 ③ R π2R a2+b2-2abcosot a2+b2+2abcosot 安培力的合力矩为 10 中国科学技术大学物理学院叶邦角整理
10 2 0 2 2 2 2 2 0 2 2 2 2 sin 1 1 2 cos 2 cos sin 1 1 2 cos 2 cos a Ib E a b ab a b ab a b I t a b ab t a b ab t ⑩ (2)(解法一) 导线框在电流 I 的磁场中旋转,受到安培力相对于轴的合力矩 M0 的作用,要使导线框保持角 速度为 的匀速旋转,所加的外力矩 M 必须满足 0 M M 0 ⑪ 正方形导线框上、下两边所受安培力的方向与转轴平行, 力矩为零,只有导线框左、右两边(分别用 A、B 表示) 受到的安培力 F1和 F2 对合力矩有贡献,如图 b 所示(俯 视图)。由②③式和安培力公式得 F1和 F2 的大小为 0 1 1 1 2 aIi F aiB r ⑫ 0 2 2 2 2 aIi F aiB r ⑬ 式中 i 为导线框中的感应电流。由欧姆定律有 2 0 2 2 2 2 sin 1 1 2 cos 2 cos a Ib tE i R R a b ab t a b ab t ⑭ 安培力的合力矩为 0 1 1 2 2 1 2 1 2 2 0 1 2 cos( ) cos( ) 2 2 sin( ) sin( ) sin( ) sin( ) M F d F d F a F a F a F a a Ii r r ⑮ 其中,d1和 d2分别为 F1和 F2与转轴之间的垂直距离,2 和 2 分别为 d1和 d2与 A、 B 连线之间的夹角。 将⑦⑧⑨⑭式代入⑮式得需要加的外力矩为 2 0 0 2 2 2 2 2 4 2 2 2 2 0 2 2 2 2 2 2 2 4 2 2 2 2 0 2 2 2 2 2 2 sin 1 1 2 cos 2 cos sin 1 1 2 cos 2 cos 4 ( )sin ( ) 4 cos a Iib t M M a b ab t a b ab t a b I t R a b ab t a b ab t a b I a b t R a b a b t ⑯ (2)(解法二) 导线框在电流 I 的磁场中旋转,受到安培力相对于轴的合力矩 M0 的作用,要使导线框保持角 速度为 的匀速旋转,所加的外力矩 M 必须满足 0 M M 0 ⑪ 此时,安培力的合力矩的功率 P0应与导线框中感应电流的功率 Pi相等,即 P P 0 i ⑫ 式中 2 2 4 2 2 2 22 0 2 2 2 2 2 sin 1 1 2 cos 2 cos i a I b tE P R R a b ab t a b ab t ⑬ 安培力的合力矩为 中国科学技术大学物理学院叶邦角整理 中国科学技术大学物理学院叶邦角整理