
第33届物理决赛理论试题 第33届物理奥林匹克竞赛决赛试题 叶邦角整理 1.(15分)山西大同某煤矿相对于秦皇岛的高度为h。质量为m,的火车载有质量为m的煤, 从大同沿大秦线铁路行驶路程!后到达秦皇岛,卸载后空车返回。从大同到秦皇岛的过程中, 火车和煤总势能的一部分克服铁轨和空气阻力做功,其余部分由发电机转换成电能,平均转 换效率为”,电能被全部储存于蓄电池中以用于返程。空车在返程中由储存的电能驱动电动 机克服重力和阻力做功,存储电能转化为对外做功的平均转换效率为?,。假设大秦线轨道 上火车平均每运行单位距离克服阻力需要做的功与运行时(火车或火车和煤)总重量成正比, 比例系数为常数山,火车由大同出发时携带的电能为零。 (1)若空车返回大同时还有剩余的电能,求该电能E。 (2)问火车至少装载质量为多少的煤,才能在不另外提供能量的条件下刚好返回大同? (3)已知火车在从大同到秦皇岛的铁轨上运行的平均速率为),请给出发电机的平均输出 功率P与题给的其它物理量的关系。 2.(15分)如图a,AB为一根匀质细杆,质量为 m,长度为人:杆上端B通过一不可伸长的软轻 64 绳悬挂到固定点O,绳长为。开始时绳和杆均 静止下垂。此后所有运动均在同一竖直面内。 (1)现对杆上的D点沿水平方向施加一瞬时冲量 I,若在施加冲量后的瞬间,B点绕悬点O转动 的角速度和杆绕其质心转动的角速度相同,求D 点到B点的距离x和B点绕悬点O转动的初始角 速度0。 图a 图b (2)设在某时刻,绳和杆与竖直方向的夹角分别 为日和8:(如图b所示),绳绕固定点O和杆绕其质心转动的角速度分别为a和。,,求绳 绕固定点0和杆绕其质心转动的角加速度a和a4:。 3.(15分)火星大气可视为仅由很稀薄的CO,组成,此大气的摩尔质量记为:,且同一高 度的大气可视为处于平衡态的理想气体。火星质量为M。(远大于火星大气总质量),半径 为R。。假设火星大气的质量密度与距离火星表面的高度h的关系为 p(h)=p1+h R 其中P。为常量,n(n>4)为常数。 (1)求火星大气温度T()随高度h变化的表达式。 (2)为了对火星表面进行探测,需将一质量为m,、质量密度较大的着陆器释放到火星表面。 在某一远小于R的高度处将该着陆器由静止开始释放,经过时间,,着陆器落到火星表面。 在着陆器下降的过程中,着陆器没有转动,火星的重力加速度和大气密度均可视为与它们在 火星表面的值相等。当着陆器下降速度大小为时,它受到的大气阻力正比于大气密度和 的乘积,比例系数为常量k。求着陆器在着陆前的瞬间速度的大小。 中国科学技术大学物理学叶邦角教授整理
第 33 届物理奥林匹克竞赛决赛试题 叶邦角整理 第33届物理决赛理论试题 中国科学技术大学物理学叶邦角教授整理 Ye Bangjiao

第33届物理决赛理论试题 4.(15分)具有一定能量、动量的光子还具有角动量。圆偏振光的光子的角动量大小为h。 光子被物体吸收后,光子的能量、动量和角动量就全部传给物体。物体吸收光子获得的角动 量可以使物体转动。科学家利用这一原理,在连续的圆偏振激光照射下,实现了纳米颗粒的 高速转动,获得了迄今为止液体环境中转速最高的微尺度转子。 如图,一金纳米球颗粒放置在两片水平光滑玻璃平板之 圆偏振激光 间,并整体(包括玻璃平板)浸在水中。一束圆偏振激光从 上往下照射到金纳米颗粒上。已知该束入射激光在真空中的 玻璃 波长2=830m,经显微物镜聚焦后(仍假设为平面波,每 个光子具有沿传播方向的角动量力)光斑直径 d=1.20×10m,功率P=20.0mW。金纳米球颗粒的半径 水 R=100nm,金的密度p=19.32×103kg/m3。忽略光在介质 玻璃☑ 界面上的反射以及玻璃、水对光的吸收等损失,仅从金纳米 颗粒吸收光子获得角动量驱动其转动的角度分析下列问题(计算结果取3位有效数字): (1)求该束激光的频率y和光强1(在传播方向上单位横截面积所传输的功率)。 (2)给出金纳米球颗粒的质量m和它绕其对称轴的转动惯量J的值。 (3)假设颗粒对光的吸收截面(颗粒吸收的光功率与入射光强之比)为6=0.123πR, 求该束激光作用在颗粒上沿旋转对称轴的力矩的大小M。 (4)已知一个以角速度为。旋转的球形颗粒(半径为r)在粘滞系数为n的液体中受到的 粘滞摩擦力矩大小为M=8πm3o。已知水的粘滞系数7=8.00×10Pas,求金纳米球颗粒 在此光束照射下达到稳定旋转时的转速(转数/秒)∫。 (5)取光开始照到处于静止状态的金纳米颗粒的瞬间为计时零点。=0,求在任意时刻1 (1>0)该颗粒转速的表达式f()。 (6)若把入射激光束换成方波脉冲激光束,脉冲宽度为工(此期间内光强仍为I),脉冲之 间的间歇时间为T,。取第一个脉冲的光开始照到颗粒的时刻为计时零点。=0,求第n个完 整脉冲周期(T+T,)后的瞬间颗粒的转速∫的表达式,并给出转速极限f的表达式。 5.(20分)许多赛车上都装有可调节的导流翼片,可以为 水平道路上的赛车提供竖直向上或向下的附加压力。如果 赛车速度的大小为v,则上述压力的大小为/。=c心,c 为一常量。当导流翼片的前方上翘时,压力方向向上:当 导流翼片的后方上翘时,压力方向向下。赛车在运动过程 中受到迎面空气的阻力,阻力大小为f,=c,,c4为一常 量。已知赛车质量为m,轮胎与路面之间的静摩擦系数为4(4,<1)。 (1)赛车在水平直道上匀速行驶时,考虑到在运动过程中轮胎的形变,路面对赛车会形成 阻力,阻力大小与车对路面的正压力大小成正比,比例系数为4。(4<4)。若导流翼片 中国科学技术大学物理学叶邦角教授整理
第33届物理决赛理论试题 中国科学技术大学物理学叶邦角教授整理 Ye Bangjiao
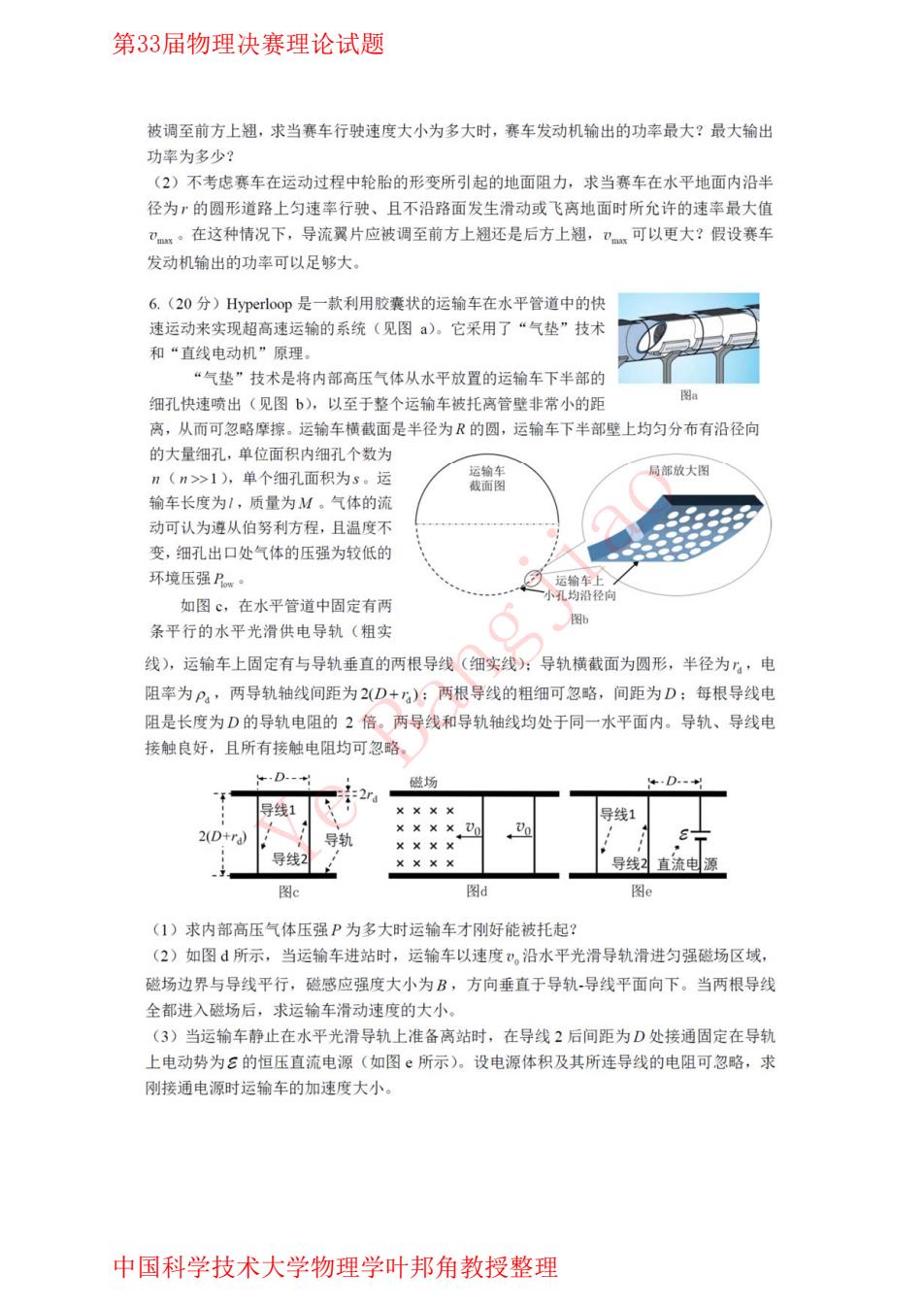
第33届物理决赛理论试题 被调至前方上翘,求当赛车行驶速度大小为多大时,赛车发动机输出的功率最大?最大输出 功率为多少? (2)不考虑赛车在运动过程中轮胎的形变所引起的地面阻力,求当赛车在水平地面内沿半 径为?的圆形道路上匀速率行驶、且不沿路面发生滑动或飞离地面时所允许的速率最大值 0x。在这种情况下,导流翼片应被调至前方上翘还是后方上翘,)可以更大?假设赛车 发动机输出的功率可以足够大。 6.(20分)Hyperloop是一款利用胶囊状的运输车在水平管道中的快 速运动来实现超高速运输的系统(见图)。它采用了“气垫”技术 和“直线电动机”原理。 “气垫”技术是将内部高压气体从水平放置的运输车下半部的 细孔快速喷出(见图b),以至于整个运输车被托离管壁非常小的距 图8 离,从而可忽略摩擦。运输车横截面是半径为R的圆,运输车下半部壁上均匀分布有沿径向 的大量细孔,单位面积内细孔个数为 n(n>1),单个细孔面积为s。运 运输车 局部放大图 截面图 输车长度为1,质量为M。气体的流 动可认为遵从伯努利方程,且温度不 变,细孔出口处气体的压强为较低的 环境压强Pw。 运输车上 小孔均沿径向 如图c,在水平管道中固定有两 图 条平行的水平光滑供电导轨(粗实 线),运输车上固定有与导轨垂直的两根导线(细实线):导轨横截面为圆形,半径为”,电 阻率为P4,两导轨轴线间距为2(D+):两根导线的粗细可忽略,间距为D;每根导线电 阻是长度为D的导轨电阻的2倍。两导线和导轨轴线均处于同一水平面内。导轨、导线电 接触良好,且所有接触电阻均可忽略 D-+ 磁场 +…D -2rd 导线1 ××Xx 导线1 2D+r) ××××0% 导轨 ××XX 导线2 ×××× 导线2 直流电源 图c 图d 图e (1)求内部高压气体压强P为多大时运输车才刚好能被托起? (2)如图所示,当运输车进站时,运输车以速度?,沿水平光滑导轨滑进匀强磁场区域, 磁场边界与导线平行,磁感应强度大小为B,方向垂直于导轨导线平面向下。当两根导线 全都进入磁场后,求运输车滑动速度的大小。 (3)当运输车静止在水平光滑导轨上准备离站时,在导线2后间距为D处接通固定在导轨 上电动势为E的恒压直流电源(如图ε所示)。设电源体积及其所连导线的电阻可忽略,求 刚接通电源时运输车的加速度大小。 中国科学技术大学物理学叶邦角教授整理
第33届物理决赛理论试题 中国科学技术大学物理学叶邦角教授整理 Ye Bangjiao

第33届物理决赛理论试题 已知某恒流闭合回路中的一圆柱形直导线段,电流沿横截面均匀分布,如图「所示,其 在空间中距导线轴线距离为的某点产生的磁感应强度方向垂直于此点和导线轴线构成的 平面,大小可用下式近似计算 B(cos+cos0.) 4r1。 其中I为电流,日、日是此点与导线段轴线两端连线与导线轴线的夹角。 可能会用到的积分公式: cdx =In bc+vc+a 其中a、b、c均为正数。 ac+Vc2+b园 7.(20分)爱因斯坦引力理论预言物质分布的变化会导致时空几何结构的波动一引力波。 为简明起见,考虑沿z轴传播的平面引力波。对于任意给定的z,在y二维空间中两个无 限邻近点(x,y)和(x+dr,y+dy)之间距离dr的表达式为 dr=+)(dx)+f(dxdy+dydx)+(1-)(dy) 引力波体现为和的变化(波动)。 (1)假设一列平面引力波传来时,和方可表示为 f=Asim[o0-31.方=00<A<1 式中,A和0分别是波的振幅和角频率,℃是引力波的传播速度(其值等于光速)。 (i)无引力波穿过时,在x-y平面上,在原点O处和与O点距离为R、与x轴夹角为 处各放置一个微探测器。求当所考虑的引力波穿过时,两个探测器之间的距离相对于R的偏 离的近似表达式。 (ⅱ)设无引力波穿过时,在y平面上,在以R为半径、原点O为圆心的圆周上放置 了一个微探测器阵列。当前述引力波存在时,可将空间坐标重新定义为(X,),使得X-Y二 维空间中邻近两点(X,Y)和(X+dX,Y+dY)距离为√(dK+(dY)。求对于给定的时刻1, 微探测器阵列在新定义的坐标系中的分布形状。 ()若一列平面引力波 f=Asin[ot-2】,f2=0 和另一列平面引力波 =Asin[o0-马+1,人=0,(0≤p<2x)是常数 同时沿z轴正向传播,问中、0满足什么条件,可使引力波对原点O处和xy二维空间中坐 标为(Rcos8,Rsin)的点处的两个微探测器之间距离的扰动的振幅达到最大或者最小? 中国科学技术大学物理学叶邦角教授整理
第33届物理决赛理论试题 中国科学技术大学物理学叶邦角教授整理 Ye Bangjiao

第33届物理决赛理论试题 (2)假定引力波的波源为双星系统。设该双星系统两星体质量均为M。取双星系统的质心 为坐标原点O',双星系统在'y二维空间中旋转。已知在特定条件下,人和5可近似表示 为 式中G为引力常量,1为在z轴上引力波探测点到0'点的距离(远大于双星系统中两星体 之间的距离),而 1,)=[x(0)+)M,I0=)y0M (x(),()、(x),以()为两星体在其质心系中的坐标。已知该引力波的频率为o,假设 引力波辐射对双星系统轨道运动的影响可忽略,求人和∫在探测点处的振幅。(在双星运行 轨道计算中可应用牛顿力学。) (1)写出电子偶素基态能量。 (2)电子偶素基态原子不稳定,可很快发生湮没而生成 两个光子: Ps→片+Y2 当基态电子偶素原子相对于实验室参照系以远小于光速 的某速度运动时发生湮没,在相对于该速度方向的偏角为 建度方向 日的方向上观测到生成的一个光子,同时在相对于光子 速度反方向的偏角为△0(△0<1)的方向上观测到另一个光子2,如图所示。 (i)求基态电子偶素原子速度0。的大小、两个光子y和,的能量E和E,的表达式: 并给出当8=骨、A0=3464×10时人£和E,的值。 ()当基态电子偶素原子静止时,求两个光子y、2各自的能量E,、E,与单个自由 电子静能之差。人 (3)当基态电子偶素原子相对于实验室参照系以与光速c可比拟的速度⑦,运动时湮没生成 两个光子,求生成的两个光子%和y2的能量E,和E2、以及光子Y2的运动方向相对于。的 方向的偏角8(如图所示)与日之间的关系式:并给出当0,=氵、8=号时E、£,和4的 值。 已知:氢原子基态能量EH=-13.60eV,电子质量m.=0.5110MeV/c2,质子与电子 的质量之比为1836。 中国科学技术大学物理学叶邦角教授整理
第33届物理决赛理论试题 中国科学技术大学物理学叶邦角教授整理 Ye Bangjiao