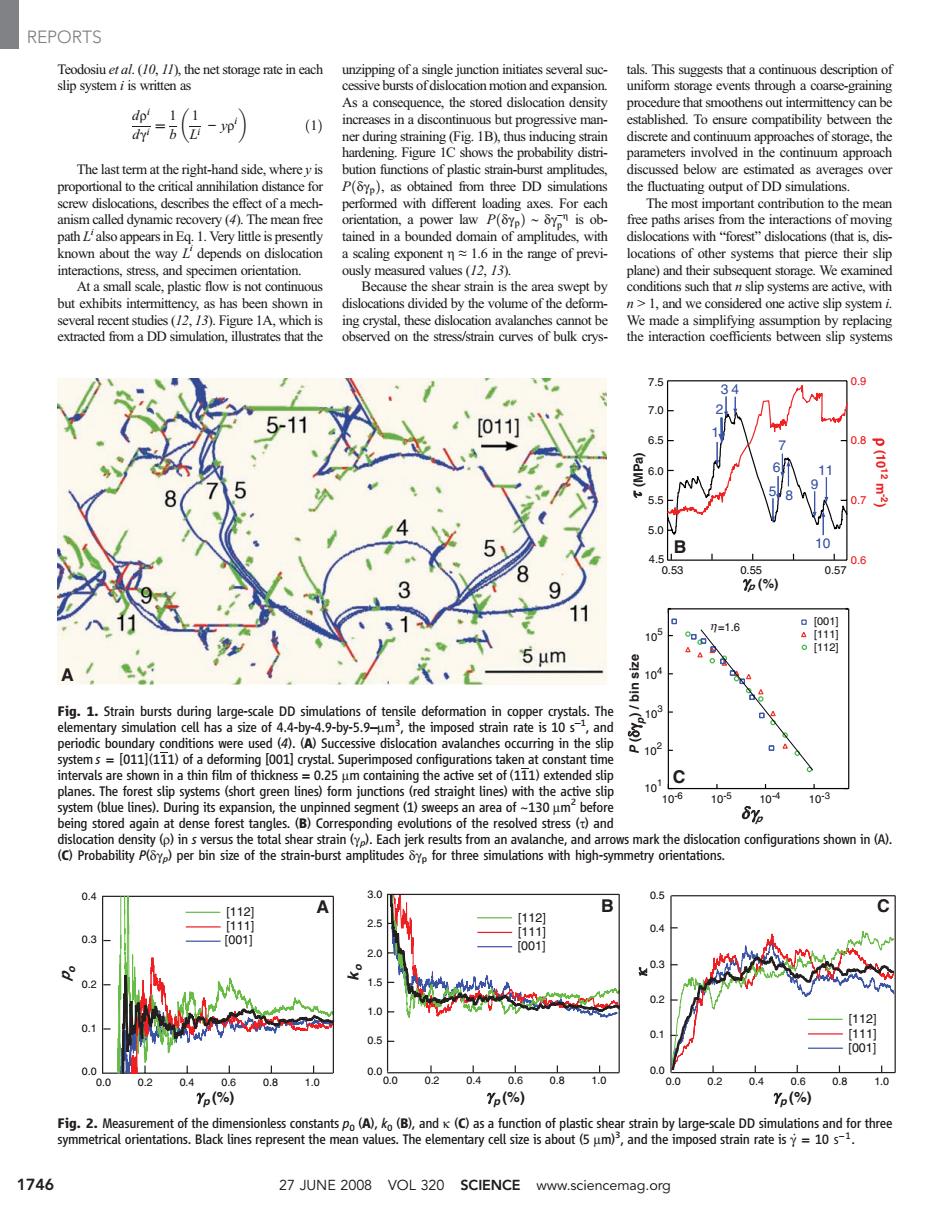
REPORTS Teodosiu etal.(10,ID),the net storage rate in each unzipping of a single junction initiates several suc- tals.This suggests that a continuous description of slip system i is written as cessive bursts of dislocation motion and expansion. uniform storage events through a coarse-graining As a consequence,the stored dislocation density procedure that smoothens out intermittency can be dp'11 =元p increases in a discontinuous but progressive man- established.To ensure compatibility between the ner during straining(Fig.1B),thus inducing strain discrete and continuum approaches of storage,the hardening.Figure 1C shows the probability distri- parameters involved in the continuum approach The last term at the right-hand side.where y is bution functions of plastic strain-burst amplitudes, discussed below are estimated as averages over proportional to the critical annihilation distance for P(p),as obtained from three DD simulations the fluctuating output of DD simulations. screw dislocations.describes the effect of a mech- performed with different loading axes.For each The most important contribution to the mean anism called dynamic recovery (4).The mean free orientation,a power law P(Yp)-Yp is ob- free paths arises from the interactions of moving path L'also appears in Eq.1.Very little is presently tained in a bounded domain of amplitudes,with dislocations with "forest"dislocations (that is.dis- known about the way L'depends on dislocation a scaling exponent n1.6 in the range of previ- locations of other systems that pierce their slip interactions,stress,and specimen orientation. ously measured values (12,/3). plane)and their subsequent storage.We examined At a small scale.plastic flow is not continuous Because the shear strain is the area swept by conditions such that nslip systems are active,with but exhibits intermittency,as has been shown in dislocations divided by the volume of the deform- n>1,and we considered one active slip system i. several recent studies (/2,/3).Figure 1A.which is ing crystal,these dislocation avalanches cannot be We made a simplifying assumption by replacing extracted from a DD simulation,illustrates that the observed on the stress/strain curves of bulk crys- the interaction coefficients between slip systems 0.9 B 10 45 0.6 0.53 0.55 0.57 2(%) 如分 =1.6 o001) 4[111] 。[112 5 um 104 Fig.1.Strain bursts during large-scale DD simulations of tensile deformation in copper crystals.The elementary simulation cell has a size of 4.4-by-4.9-by-5.9-m,the imposed strain rate is 10 s and periodic boundary conditions were used (4).(A)Successive dislocation avalanches occurring in the slip systems =[011](111)of a deforming [001]crystal.Superimposed configurations taken at constant time 0102 intervals are shown in a thin film of thickness =0.25 um containing the active set of (111)extended slip C planes.The forest slip systems(short green lines)form junctions (red straight lines)with the active slip 10 10-6 10-5 104 system (blue lines).During its expansion,the unpinned segment(1)sweeps an area of-130 um2before 10-3 being stored again at dense forest tangles.(B)Corresponding evolutions of the resolved stress (t)and SYp dislocation density (p)in s versus the total shear strain ()Each jerk results from an avalanche,and arrows mark the dislocation configurations shown in(A). (C)Probability P(Yp)per bin size of the strain-burst amplitudes Yp for three simulations with high-symmetry orientations. 0.4 3.0 0.5 [112 B [112] [111 2.5 [111 0.4 0.3 [001] [001] 2.0 0.3 02 5 0.2 1.0 [112 0.1 1 0.5 111 001] 0.0 0.0 0.0 0.0 0.2 0.4 0.6 0.8 00 02 0.40.6 0.8 0.0 0.2 0.4 0.6 0.8 1.0 Yp(%) Yp(%) Yp(%) Fig.2.Measurement of the dimensionless constants Po(A),ko(B),and K(C)as a function of plastic shear strain by large-scale DD simulations and for three symmetrical orientations.Black lines represent the mean values.The elementary cell size is about (5 um),and the imposed strain rate isy=10 s-1. 1746 27 JUNE 2008 VOL 320 SCIENCE www.sciencemag.orgTeodosiu et al. (10, 11), the net storage rate in each slip system i is written as dri dgi ¼ 1 b 1 Li − yri  ð1Þ The last term at the right-hand side, where y is proportional to the critical annihilation distance for screw dislocations, describes the effect of a mech￾anism called dynamic recovery (4). The mean free path Li also appears in Eq. 1. Very little is presently known about the way Li depends on dislocation interactions, stress, and specimen orientation. At a small scale, plastic flow is not continuous but exhibits intermittency, as has been shown in several recent studies (12, 13). Figure 1A, which is extracted from a DD simulation, illustrates that the unzipping of a single junction initiates several suc￾cessive bursts of dislocation motion and expansion. As a consequence, the stored dislocation density increases in a discontinuous but progressive man￾ner during straining (Fig. 1B), thus inducing strain hardening. Figure 1C shows the probability distri￾bution functions of plastic strain-burst amplitudes, PðdgpÞ, as obtained from three DD simulations performed with different loading axes. For each orientation, a power law PðdgpÞ ∼ dg−h p is ob￾tained in a bounded domain of amplitudes, with a scaling exponent h ≈ 1.6 in the range of previ￾ously measured values (12, 13). Because the shear strain is the area swept by dislocations divided by the volume of the deform￾ing crystal, these dislocation avalanches cannot be observed on the stress/strain curves of bulk crys￾tals. This suggests that a continuous description of uniform storage events through a coarse-graining procedure that smoothens out intermittency can be established. To ensure compatibility between the discrete and continuum approaches of storage, the parameters involved in the continuum approach discussed below are estimated as averages over the fluctuating output of DD simulations. The most important contribution to the mean free paths arises from the interactions of moving dislocations with “forest” dislocations (that is, dis￾locations of other systems that pierce their slip plane) and their subsequent storage. We examined conditions such that n slip systems are active, with n > 1, and we considered one active slip system i. We made a simplifying assumption by replacing the interaction coefficients between slip systems A 1 2 3 4 5 7 9 10 6 11 8 (MPa) 7.5 7.0 6.5 6.0 5.5 5.0 4.5 0.9 0.8 0.7 0.6 ρ (1012 m-2) γp B τ 0.53 0.55 0.57 δγp 10-6 10-3 10-4 10-5 101 105 104 103 102 [001] [111] [112] P (δγp) / bin size η C =1.6 (%) Fig. 1. Strain bursts during large-scale DD simulations of tensile deformation in copper crystals. The elementary simulation cell has a size of 4.4-by-4.9-by-5.9–mm3 , the imposed strain rate is 10 s–1 , and periodic boundary conditions were used (4). (A) Successive dislocation avalanches occurring in the slip system s = [011](111) of a deforming [001] crystal. Superimposed configurations taken at constant time intervals are shown in a thin film of thickness = 0.25 mm containing the active set of (111) extended slip planes. The forest slip systems (short green lines) form junctions (red straight lines) with the active slip system (blue lines). During its expansion, the unpinned segment (1) sweeps an area of ~130 mm2 before being stored again at dense forest tangles. (B) Corresponding evolutions of the resolved stress (t) and dislocation density (r) in s versus the total shear strain (gp). Each jerk results from an avalanche, and arrows mark the dislocation configurations shown in (A). (C) Probability P(dgp) per bin size of the strain-burst amplitudes dgp for three simulations with high-symmetry orientations. 0.0 0.2 0.4 0.6 0.8 1.0 0.5 0.4 0.3 0.2 0.1 0.0 C γ p (%) γ p (%) γ p (%) κ 0.0 0.2 0.4 0.6 0.8 1.0 3.0 2.5 2.0 1.5 1.0 0.5 0.0 B ko [112] [111] [001] 0.0 0.2 0.4 0.6 0.8 1.0 0.4 0.3 0.2 0.1 0.0 A po [112] [111] [001] [112] [111] [001] Fig. 2. Measurement of the dimensionless constants p0 (A), k0 (B), and k (C) as a function of plastic shear strain by large-scale DD simulations and for three symmetrical orientations. Black lines represent the mean values. The elementary cell size is about (5 mm)3 , and the imposed strain rate is g˙ = 10 s −1. 1746 27 JUNE 2008 VOL 320 SCIENCE www.sciencemag.org REPORTS