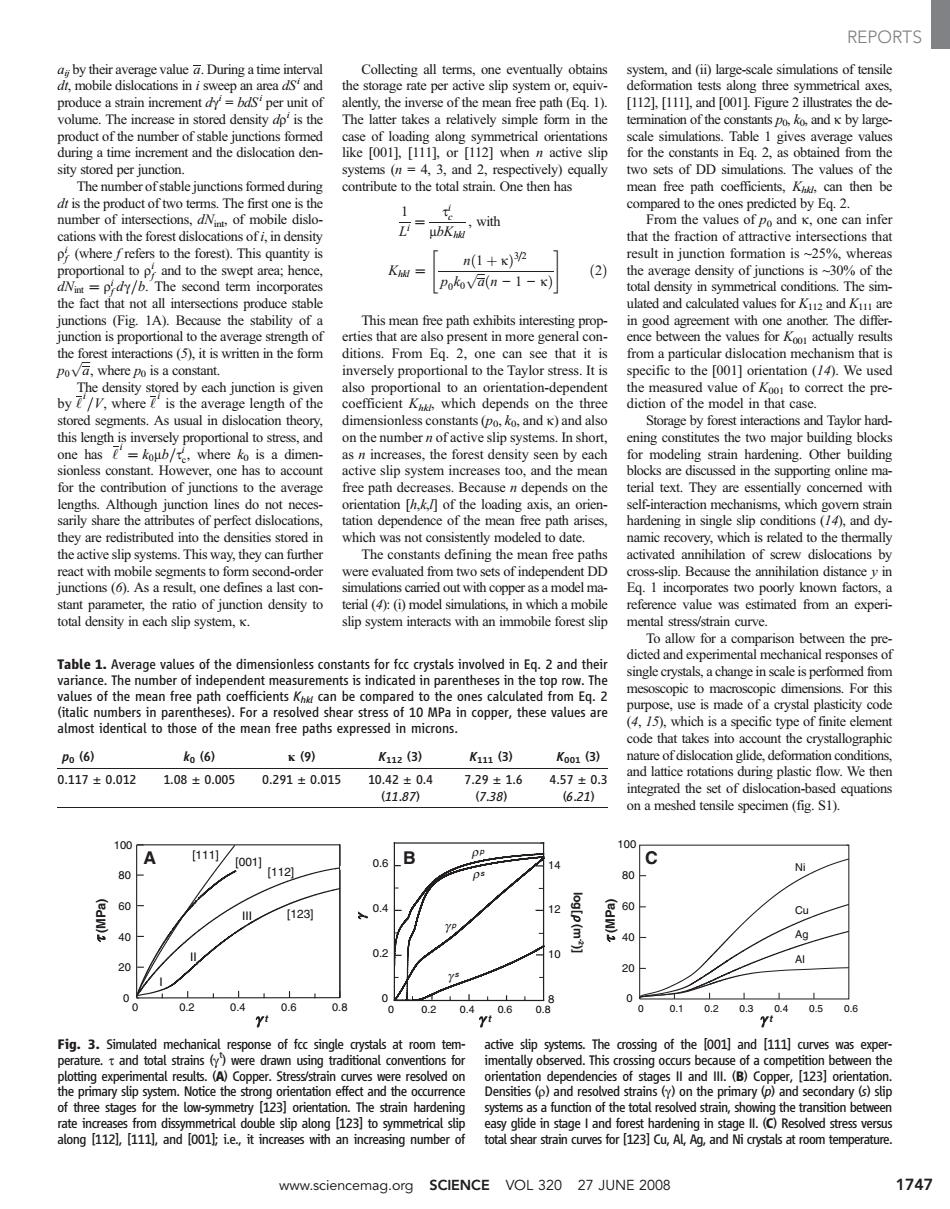
REPORTS a by their average value a.During a time interval Collecting all terms,one eventually obtains system,and (ii)large-scale simulations of tensile dt,mobile dislocations in i sweep an area dsand the storage rate per active slip system or,equiv- deformation tests along three symmetrical axes, produce a strain increment dy'=bds'per unit of alently,the inverse of the mean free path (Eq.1). [1121.[111],and [0011.Figure 2 illustrates the de- volume.The increase in stored density dp'is the The latter takes a relatively simple form in the termination of the constants po.ko.and K by large- product of the number of stable junctions formed case of loading along symmetrical orientations scale simulations.Table 1 gives average values during a time increment and the dislocation den- like [001],[111],or [112]when n active slip for the constants in Eq.2,as obtained from the sity stored per junction. systems (n=4,3,and 2,respectively)equally two sets of DD simulations.The values of the The number of stable junctions formed during contribute to the total strain.One then has mean free path coefficients,K,can then be dt is the product of two terms.The first one is the compared to the ones predicted by Eq.2. number of intersections,dNn of mobile dislo- with From the values of po and K,one can infer cations with the forest dislocations of i,in density L ubK that the fraction of attractive intersections that p(where frefers to the forest).This quantity is n(1+x)2 result in junction formation is ~25%,whereas proportional to p'and to the swept area;hence, K 2) the average density of junctions is~30%of the dNimt =pfdy/b.The second term incorporates Pokova(n-1-K) total density in symmetrical conditions.The sim- the fact that not all intersections produce stable ulated and calculated values for Ki2 and Ki are junctions (Fig.1A).Because the stability of a This mean free path exhibits interesting prop- in good agreement with one another.The differ- junction is proportional to the average strength of erties that are also present in more general con- ence between the values for Koo actually results the forest interactions (5).it is written in the form ditions.From Eq.2,one can see that it is from a particular dislocation mechanism that is pova,where po is a constant. inversely proportional to the Taylor stress.It is specific to the [001]orientation (/4).We used The density stored by each junction is given also proportional to an orientation-dependent the measured value of Koor to correct the pre- by e/V,where e'is the average length of the coefficient Kik,which depends on the three diction of the model in that case. stored segments.As usual in dislocation theory, dimensionless constants (po,ko,and K)and also Storage by forest interactions and Taylor hard- this length is inversely proportional to stress,and on the number n ofactive slip systems.In short, ening constitutes the two major building blocks one has e'=koub/te,where ko is a dimen- as n increases,the forest density seen by each for modeling strain hardening.Other building sionless constant.However.one has to account active slip system increases too.and the mean blocks are discussed in the supporting online ma- for the contribution of junctions to the average free path decreases.Because n depends on the terial text.They are essentially concemned with lengths.Although junction lines do not neces- orientation [h,]of the loading axis,an orien- self-interaction mechanisms,which govern strain sarily share the attributes of perfect dislocations tation dependence of the mean free path arises. hardening in single slip conditions (/4),and dy- they are redistributed into the densities stored in which was not consistently modeled to date. namic recovery,which is related to the thermally the active slip systems.This way,they can further The constants defining the mean free paths activated annihilation of screw dislocations by react with mobile segments to form second-order were evaluated from two sets of independent DD cross-slip.Because the annihilation distanceyin junctions (6).As a result,one defines a last con- simulations caried out with copper as a model ma- Eq.1 incorporates two poorly known factors,a stant parameter,the ratio of junction density to terial (4):(1)model simulations,in which a mobile reference value was estimated from an experi- total density in each slip system,K. slip system interacts with an immobile forest slip mental stress/strain curve. To allow for a comparison between the pre- Table 1.Average values of the dimensionless constants for fcc crystals involved in Eq.2 and their dicted and experimental mechanical responses of single crystals,a change in scale is performed from variance.The number of independent measurements is indicated in parentheses in the top row.The values of the mean free path coefficients K can be compared to the ones calculated from Eq.2 mesoscopic to macroscopic dimensions.For this (italic numbers in parentheses).For a resolved shear stress of 10 MPa in copper,these values are purpose,use is made of a crystal plasticity code almost identical to those of the mean free paths expressed in microns. (4,/5),which is a specific type of finite element code that takes into account the crystallographic Po(6) k(6) K(9) K112(3) K11(3) Koo1(3) nature of dislocation glide.deformation conditions. 0.117±0.012 1.08±0.005 0.291±0.015 10.42±0.4 7.29±1.6 4.57±0.3 and lattice rotations during plastic flow.We then 11.87八 (738) (6.21) integrated the set of dislocation-based equations on a meshed tensile specimen (fig.S1). 100 100 [111] [001] B PP 0.6 C 80 【1121 ps 80 化 60 0.4 log[p(m)] 60 [123) Cu 40 40 Ag 0.2 10 0 20 0 0 0 0 0.2 0.4 0.6 0.8 0 0.2 0.4 0.6 0.8 0 0.1 0.2 0.30.40.50.6 yt Yi Fig.3.Simulated mechanical response of fcc single crystals at room tem- active slip systems.The crossing of the [001]and [111]curves was exper- perature.t and total strains (y)were drawn using traditional conventions for imentally observed.This crossing occurs because of a competition between the plotting experimental results.(A)Copper.Stress/strain curves were resolved on orientation dependencies of stages ll and Ill.(B)Copper,[123]orientation. the primary slip system.Notice the strong orientation effect and the occurrence Densities (p)and resolved strains (y)on the primary (p)and secondary (s)slip of three stages for the low-symmetry [123]orientation.The strain hardening systems as a function of the total resolved strain,showing the transition between rate increases from dissymmetrical double slip along [123]to symmetrical slip easy glide in stage I and forest hardening in stage ll.(C)Resolved stress versus along [112],[111],and [001];i.e.,it increases with an increasing number of total shear strain curves for [123]Cu,Al,Ag,and Ni crystals at room temperature. www.sciencemag.org SCIENCE VOL 320 27 JUNE 2008 1747aij by their average value a. During a time interval dt, mobile dislocations in i sweep an area dSi and produce a strain increment dgi = bdSi per unit of volume. The increase in stored density dri is the product of the number of stable junctions formed during a time increment and the dislocation den￾sity stored per junction. The number of stable junctions formed during dt is the product of two terms. The first one is the number of intersections, dNint, of mobile dislo￾cations with the forest dislocations of i, in density ri f (where f refers to the forest). This quantity is proportional to ri f and to the swept area; hence, dNint ¼ ri f dg=b. The second term incorporates the fact that not all intersections produce stable junctions (Fig. 1A). Because the stability of a junction is proportional to the average strength of the forest interactions (5), it is written in the form p0 ffiffiffi a p , where p0 is a constant. The density stored by each junction is given by ‘ i =V, where ‘ i is the average length of the stored segments. As usual in dislocation theory, this length is inversely proportional to stress, and one has ‘ i ¼ k0mb=ti c, where k0 is a dimen￾sionless constant. However, one has to account for the contribution of junctions to the average lengths. Although junction lines do not neces￾sarily share the attributes of perfect dislocations, they are redistributed into the densities stored in the active slip systems. This way, they can further react with mobile segments to form second-order junctions (6). As a result, one defines a last con￾stant parameter, the ratio of junction density to total density in each slip system, k. Collecting all terms, one eventually obtains the storage rate per active slip system or, equiv￾alently, the inverse of the mean free path (Eq. 1). The latter takes a relatively simple form in the case of loading along symmetrical orientations like [001], [111], or [112] when n active slip systems (n = 4, 3, and 2, respectively) equally contribute to the total strain. One then has 1 Li ¼ ti c mbKhkl , with Khkl ¼ nð1 þ kÞ 3=2 p0k0 ffiffiffi a p ðn − 1 − kÞ " # ð2Þ This mean free path exhibits interesting prop￾erties that are also present in more general con￾ditions. From Eq. 2, one can see that it is inversely proportional to the Taylor stress. It is also proportional to an orientation-dependent coefficient Khkl, which depends on the three dimensionless constants (p0, k0, and k) and also on the number n of active slip systems. In short, as n increases, the forest density seen by each active slip system increases too, and the mean free path decreases. Because n depends on the orientation [h,k,l] of the loading axis, an orien￾tation dependence of the mean free path arises, which was not consistently modeled to date. The constants defining the mean free paths were evaluated from two sets of independent DD simulations carried out with copper as a model ma￾terial (4): (i) model simulations, in which a mobile slip system interacts with an immobile forest slip system, and (ii) large-scale simulations of tensile deformation tests along three symmetrical axes, [112], [111], and [001]. Figure 2 illustrates the de￾termination of the constants p0, k0, and k by large￾scale simulations. Table 1 gives average values for the constants in Eq. 2, as obtained from the two sets of DD simulations. The values of the mean free path coefficients, Khkl, can then be compared to the ones predicted by Eq. 2. From the values of p0 and k, one can infer that the fraction of attractive intersections that result in junction formation is ~25%, whereas the average density of junctions is ~30% of the total density in symmetrical conditions. The sim￾ulated and calculated values for K112 and K111 are in good agreement with one another. The differ￾ence between the values for K001 actually results from a particular dislocation mechanism that is specific to the [001] orientation (14). We used the measured value of K001 to correct the pre￾diction of the model in that case. Storage by forest interactions and Taylor hard￾ening constitutes the two major building blocks for modeling strain hardening. Other building blocks are discussed in the supporting online ma￾terial text. They are essentially concerned with self-interaction mechanisms, which govern strain hardening in single slip conditions (14), and dy￾namic recovery, which is related to the thermally activated annihilation of screw dislocations by cross-slip. Because the annihilation distance y in Eq. 1 incorporates two poorly known factors, a reference value was estimated from an experi￾mental stress/strain curve. To allow for a comparison between the pre￾dicted and experimental mechanical responses of single crystals, a change in scale is performed from mesoscopic to macroscopic dimensions. For this purpose, use is made of a crystal plasticity code (4, 15), which is a specific type of finite element code that takes into account the crystallographic nature of dislocation glide, deformation conditions, and lattice rotations during plastic flow. We then integrated the set of dislocation-based equations on a meshed tensile specimen (fig. S1). Table 1. Average values of the dimensionless constants for fcc crystals involved in Eq. 2 and their variance. The number of independent measurements is indicated in parentheses in the top row. The values of the mean free path coefficients Khkl can be compared to the ones calculated from Eq. 2 (italic numbers in parentheses). For a resolved shear stress of 10 MPa in copper, these values are almost identical to those of the mean free paths expressed in microns. p0 (6) k0 (6) k (9) K112 (3) K111 (3) K001 (3) 0.117 ± 0.012 1.08 ± 0.005 0.291 ± 0.015 10.42 ± 0.4 (11.87) 7.29 ± 1.6 (7.38) 4.57 ± 0.3 (6.21) 0 20 40 60 80 100 0 0.2 0.4 0.6 0.8 [001] [111] [112] [123] I II III A γ t γ t γ t (MPa) τ (MPa) τ 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0.8 γ log[ (m-2)] 8 10 12 14 ρp ρs γ p γ s B ρ 0 20 40 60 80 100 0 0.1 0.2 0.3 0.4 0.5 0.6 C Ni Cu Ag Al Fig. 3. Simulated mechanical response of fcc single crystals at room tem￾perature. t and total strains (gt ) were drawn using traditional conventions for plotting experimental results. (A) Copper. Stress/strain curves were resolved on the primary slip system. Notice the strong orientation effect and the occurrence of three stages for the low-symmetry [123] orientation. The strain hardening rate increases from dissymmetrical double slip along [123] to symmetrical slip along [112], [111], and [001]; i.e., it increases with an increasing number of active slip systems. The crossing of the [001] and [111] curves was exper￾imentally observed. This crossing occurs because of a competition between the orientation dependencies of stages II and III. (B) Copper, [123] orientation. Densities (r) and resolved strains (g) on the primary (p) and secondary (s) slip systems as a function of the total resolved strain, showing the transition between easy glide in stage I and forest hardening in stage II. (C) Resolved stress versus total shear strain curves for [123] Cu, Al, Ag, and Ni crystals at room temperature. www.sciencemag.org SCIENCE VOL 320 27 JUNE 2008 1747 REPORTS