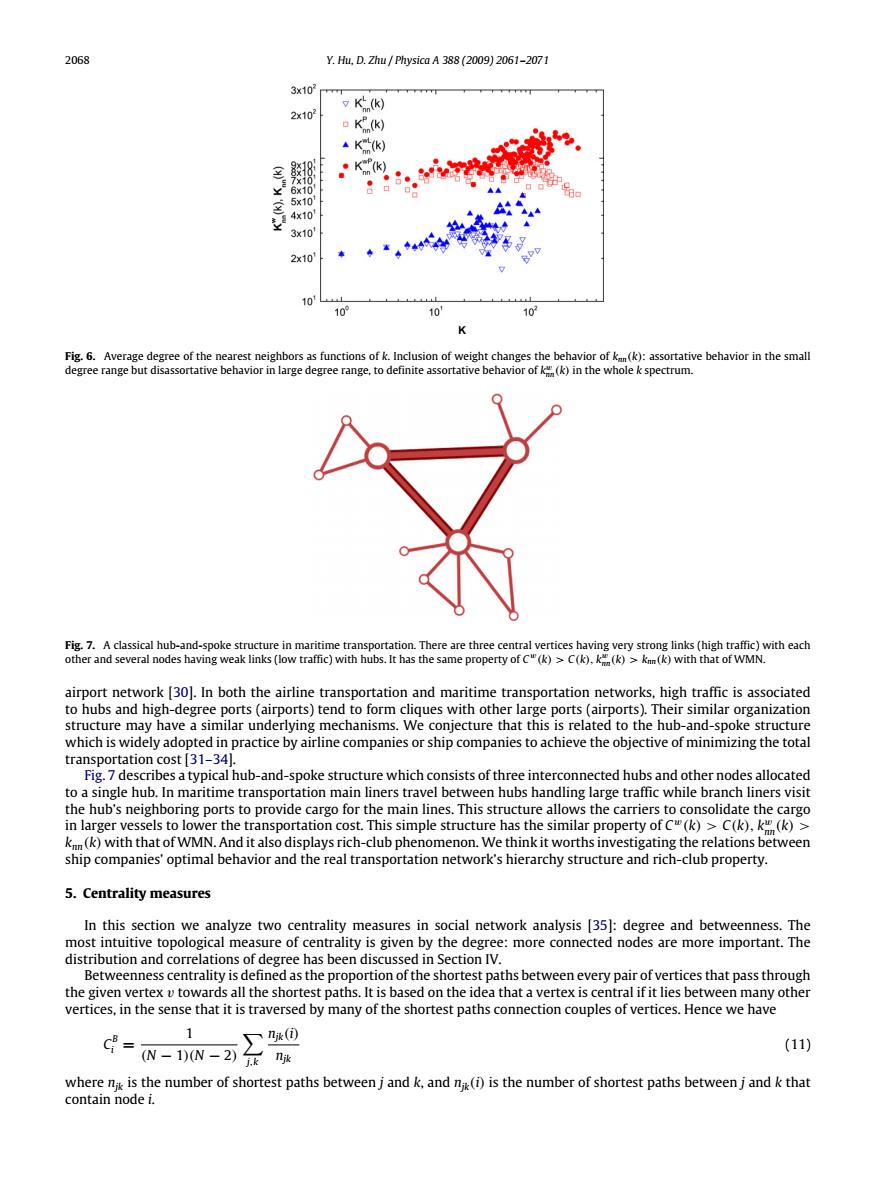
2068 Y.Hu,D.Zhu Physica A 388(2009)2061-2071 3x10 K(k) 2x102 K(k) ▲Kk) K 5x10 4x10 3x10 2x10 10 10 10' 10 K Fig.6.Average degree of the nearest neighbors as functions of k.Inclusion of weight changes the behavior of k(k):assortative behavior in the small degree range but disassortative behavior in large degree range,to definite assortative behavior of k(k)in the whole k spectrum. Fig.7.A classical hub-and-spoke structure in maritime transportation.There are three central vertices having very strong links (high traffic)with each other and several nodes having weak links (low traffic)with hubs.It has the same property of c(k)>C(k).k(k)>knn(k)with that of WMN. airport network[30].In both the airline transportation and maritime transportation networks,high traffic is associated to hubs and high-degree ports(airports)tend to form cliques with other large ports(airports).Their similar organization structure may have a similar underlying mechanisms.We conjecture that this is related to the hub-and-spoke structure which is widely adopted in practice by airline companies or ship companies to achieve the objective of minimizing the total transportation cost [31-34]. Fig.7 describes a typical hub-and-spoke structure which consists of three interconnected hubs and other nodes allocated to a single hub.In maritime transportation main liners travel between hubs handling large traffic while branch liners visit the hub's neighboring ports to provide cargo for the main lines.This structure allows the carriers to consolidate the cargo in larger vessels to lower the transportation cost.This simple structure has the similar property of C"(k)>C(k),k(k)> kn(k)with that of WMN.And it also displays rich-club phenomenon.We think it worths investigating the relations between ship companies'optimal behavior and the real transportation network's hierarchy structure and rich-club property. 5.Centrality measures In this section we analyze two centrality measures in social network analysis 35:degree and betweenness.The most intuitive topological measure of centrality is given by the degree:more connected nodes are more important.The distribution and correlations of degree has been discussed in Section IV. Betweenness centrality is defined as the proportion of the shortest paths between every pair of vertices that pass through the given vertex v towards all the shortest paths.It is based on the idea that a vertex is central if it lies between many other vertices,in the sense that it is traversed by many of the shortest paths connection couples of vertices.Hence we have 1 C= 下nk(0 (N -1)(N-2)j.K jk (11) where nik is the number of shortest paths between j and k,and n(i)is the number of shortest paths between j and k that contain node i.2068 Y. Hu, D. Zhu / Physica A 388 (2009) 2061–2071 Fig. 6. Average degree of the nearest neighbors as functions of k. Inclusion of weight changes the behavior of knn(k): assortative behavior in the small degree range but disassortative behavior in large degree range, to definite assortative behavior of k w nn(k) in the whole k spectrum. Fig. 7. A classical hub-and-spoke structure in maritime transportation. There are three central vertices having very strong links (high traffic) with each other and several nodes having weak links (low traffic) with hubs. It has the same property of C w(k) > C(k), k w nn(k) > knn(k) with that of WMN. airport network [30]. In both the airline transportation and maritime transportation networks, high traffic is associated to hubs and high-degree ports (airports) tend to form cliques with other large ports (airports). Their similar organization structure may have a similar underlying mechanisms. We conjecture that this is related to the hub-and-spoke structure which is widely adopted in practice by airline companies or ship companies to achieve the objective of minimizing the total transportation cost [31–34]. Fig. 7 describes a typical hub-and-spoke structure which consists of three interconnected hubs and other nodes allocated to a single hub. In maritime transportation main liners travel between hubs handling large traffic while branch liners visit the hub’s neighboring ports to provide cargo for the main lines. This structure allows the carriers to consolidate the cargo in larger vessels to lower the transportation cost. This simple structure has the similar property of C w(k) > C(k), k w nn(k) > knn(k) with that of WMN. And it also displays rich-club phenomenon. We think it worths investigating the relations between ship companies’ optimal behavior and the real transportation network’s hierarchy structure and rich-club property. 5. Centrality measures In this section we analyze two centrality measures in social network analysis [35]: degree and betweenness. The most intuitive topological measure of centrality is given by the degree: more connected nodes are more important. The distribution and correlations of degree has been discussed in Section IV. Betweenness centrality is defined as the proportion of the shortest paths between every pair of vertices that pass through the given vertex v towards all the shortest paths. It is based on the idea that a vertex is central if it lies between many other vertices, in the sense that it is traversed by many of the shortest paths connection couples of vertices. Hence we have C B i = 1 (N − 1)(N − 2) X j,k njk(i) njk (11) where njk is the number of shortest paths between j and k, and njk(i) is the number of shortest paths between j and k that contain node i