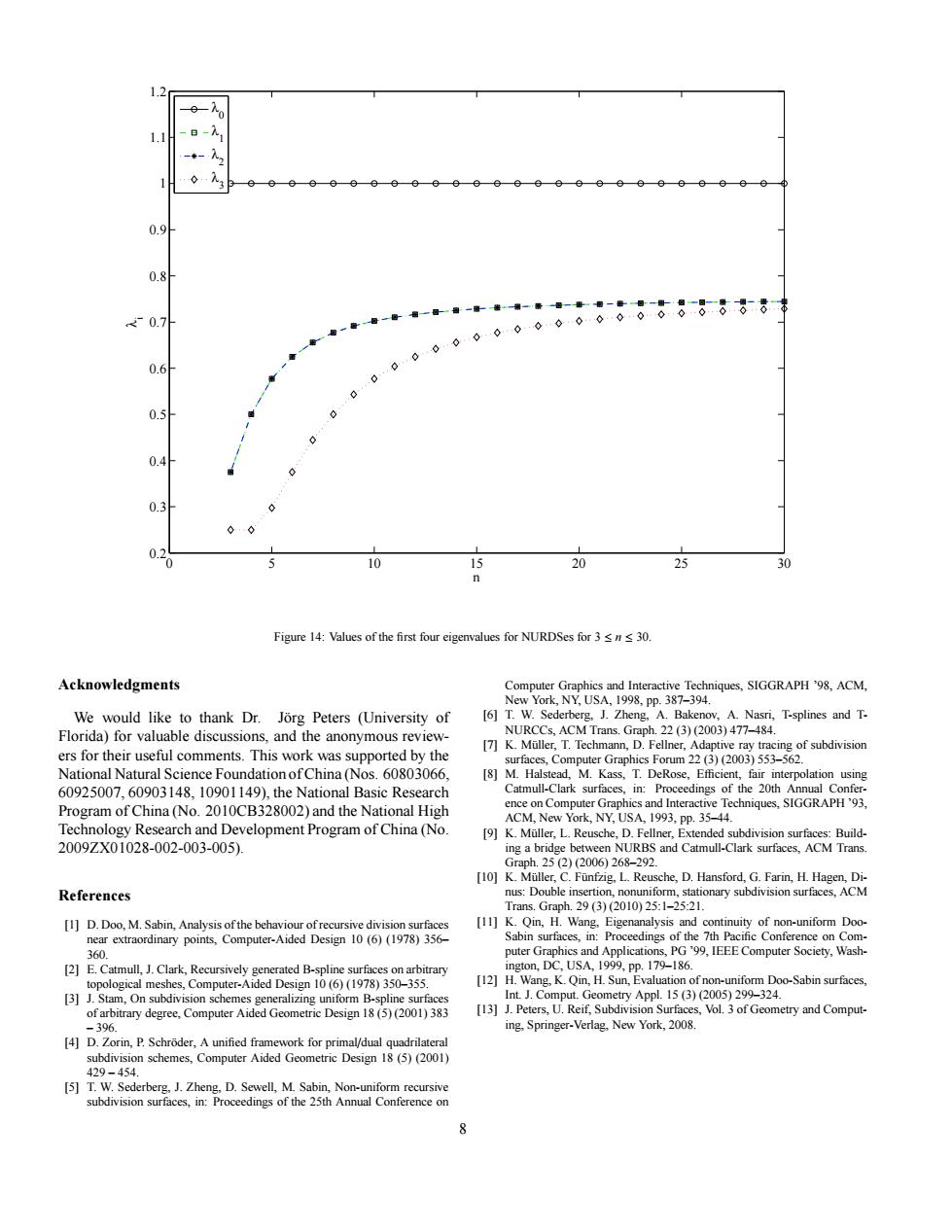
1.2 0.8 <0.7 06 0.s 0.4 10 20 Figure 14:Values of the frst four eigenvaues for NURDSes for Acknowledgments uCs.SIGGRAPH 98.ACM (20 。0 USA.1993. 2092X07028.002-003.00 velopment Program of China (N References h2932010,251-252 .U.Re etry and Comput 0 5 10 15 20 25 30 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 n λ i λ 0 λ 1 λ 2 λ 3 Figure 14: Values of the first four eigenvalues for NURDSes for 3 ≤ n ≤ 30. Acknowledgments We would like to thank Dr. J¨org Peters (University of Florida) for valuable discussions, and the anonymous review￾ers for their useful comments. This work was supported by the National Natural Science Foundation of China (Nos. 60803066, 60925007, 60903148, 10901149), the National Basic Research Program of China (No. 2010CB328002) and the National High Technology Research and Development Program of China (No. 2009ZX01028-002-003-005). References [1] D. Doo, M. Sabin, Analysis of the behaviour of recursive division surfaces near extraordinary points, Computer-Aided Design 10 (6) (1978) 356– 360. [2] E. Catmull, J. Clark, Recursively generated B-spline surfaces on arbitrary topological meshes, Computer-Aided Design 10 (6) (1978) 350–355. [3] J. Stam, On subdivision schemes generalizing uniform B-spline surfaces of arbitrary degree, Computer Aided Geometric Design 18 (5) (2001) 383 – 396. [4] D. Zorin, P. Schr¨oder, A unified framework for primal/dual quadrilateral subdivision schemes, Computer Aided Geometric Design 18 (5) (2001) 429 – 454. [5] T. W. Sederberg, J. Zheng, D. Sewell, M. Sabin, Non-uniform recursive subdivision surfaces, in: Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’98, ACM, New York, NY, USA, 1998, pp. 387–394. [6] T. W. Sederberg, J. Zheng, A. Bakenov, A. Nasri, T-splines and T￾NURCCs, ACM Trans. Graph. 22 (3) (2003) 477–484. [7] K. M¨uller, T. Techmann, D. Fellner, Adaptive ray tracing of subdivision surfaces, Computer Graphics Forum 22 (3) (2003) 553–562. [8] M. Halstead, M. Kass, T. DeRose, Efficient, fair interpolation using Catmull-Clark surfaces, in: Proceedings of the 20th Annual Confer￾ence on Computer Graphics and Interactive Techniques, SIGGRAPH ’93, ACM, New York, NY, USA, 1993, pp. 35–44. [9] K. M¨uller, L. Reusche, D. Fellner, Extended subdivision surfaces: Build￾ing a bridge between NURBS and Catmull-Clark surfaces, ACM Trans. Graph. 25 (2) (2006) 268–292. [10] K. M¨uller, C. F¨unfzig, L. Reusche, D. Hansford, G. Farin, H. Hagen, Di￾nus: Double insertion, nonuniform, stationary subdivision surfaces, ACM Trans. Graph. 29 (3) (2010) 25:1–25:21. [11] K. Qin, H. Wang, Eigenanalysis and continuity of non-uniform Doo￾Sabin surfaces, in: Proceedings of the 7th Pacific Conference on Com￾puter Graphics and Applications, PG ’99, IEEE Computer Society, Wash￾ington, DC, USA, 1999, pp. 179–186. [12] H. Wang, K. Qin, H. Sun, Evaluation of non-uniform Doo-Sabin surfaces, Int. J. Comput. Geometry Appl. 15 (3) (2005) 299–324. [13] J. Peters, U. Reif, Subdivision Surfaces, Vol. 3 of Geometry and Comput￾ing, Springer-Verlag, New York, 2008. 8