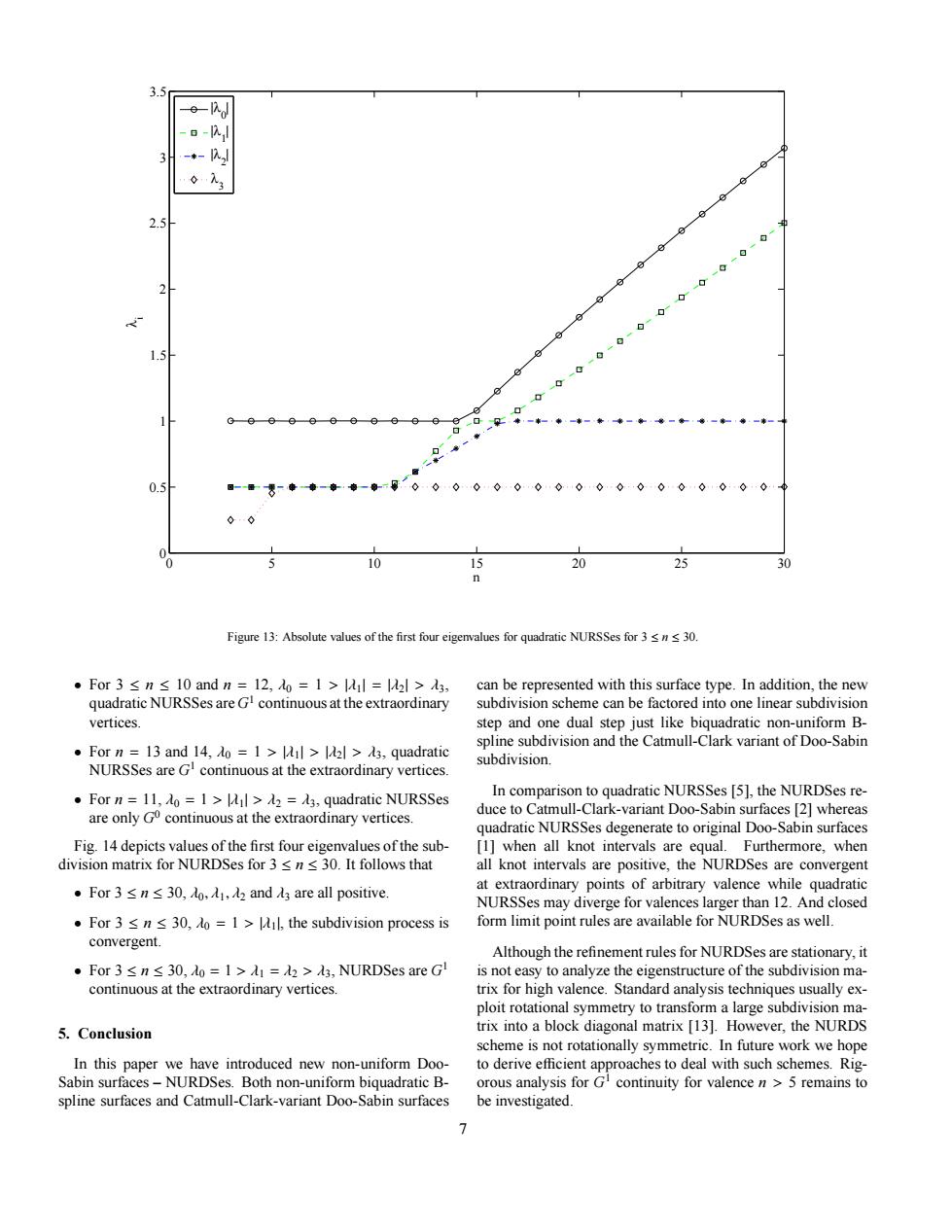
25 1.5 0.5 。8◆◆-◆-08000099000000000000 10 20 2 Fipure 13:Absolute values of the first four eigemnlues for qundratie NURSSes for 3sws 30. vertices. · and the CamullCark varamt o Do vision and th ]when all knot inte ls ar urthermore,whe ·For3≤m≤30，o.d4,andare all positive. ordinary P nts of arbitrary valene e while quadrat ·For3≤n≤30.o=1>Al.the subdivision process is convergent. notor high ploitTotat 5.Conclusion 31 In future work we hope variant Doo 0 5 10 15 20 25 30 0 0.5 1 1.5 2 2.5 3 3.5 n λ i |λ 0 | |λ 1 | |λ 2 | λ 3 Figure 13: Absolute values of the first four eigenvalues for quadratic NURSSes for 3 ≤ n ≤ 30. • For 3 ≤ n ≤ 10 and n = 12, λ0 = 1 > |λ1| = |λ2| > λ3, quadratic NURSSes are G 1 continuous at the extraordinary vertices. • For n = 13 and 14, λ0 = 1 > |λ1| > |λ2| > λ3, quadratic NURSSes are G 1 continuous at the extraordinary vertices. • For n = 11, λ0 = 1 > |λ1| > λ2 = λ3, quadratic NURSSes are only G 0 continuous at the extraordinary vertices. Fig. 14 depicts values of the first four eigenvalues of the sub￾division matrix for NURDSes for 3 ≤ n ≤ 30. It follows that • For 3 ≤ n ≤ 30, λ0, λ1, λ2 and λ3 are all positive. • For 3 ≤ n ≤ 30, λ0 = 1 > |λ1|, the subdivision process is convergent. • For 3 ≤ n ≤ 30, λ0 = 1 > λ1 = λ2 > λ3, NURDSes are G 1 continuous at the extraordinary vertices. 5. Conclusion In this paper we have introduced new non-uniform Doo￾Sabin surfaces – NURDSes. Both non-uniform biquadratic B￾spline surfaces and Catmull-Clark-variant Doo-Sabin surfaces can be represented with this surface type. In addition, the new subdivision scheme can be factored into one linear subdivision step and one dual step just like biquadratic non-uniform B￾spline subdivision and the Catmull-Clark variant of Doo-Sabin subdivision. In comparison to quadratic NURSSes [5], the NURDSes re￾duce to Catmull-Clark-variant Doo-Sabin surfaces [2] whereas quadratic NURSSes degenerate to original Doo-Sabin surfaces [1] when all knot intervals are equal. Furthermore, when all knot intervals are positive, the NURDSes are convergent at extraordinary points of arbitrary valence while quadratic NURSSes may diverge for valences larger than 12. And closed form limit point rules are available for NURDSes as well. Although the refinement rules for NURDSes are stationary, it is not easy to analyze the eigenstructure of the subdivision ma￾trix for high valence. Standard analysis techniques usually ex￾ploit rotational symmetry to transform a large subdivision ma￾trix into a block diagonal matrix [13]. However, the NURDS scheme is not rotationally symmetric. In future work we hope to derive efficient approaches to deal with such schemes. Rig￾orous analysis for G 1 continuity for valence n > 5 remains to be investigated. 7