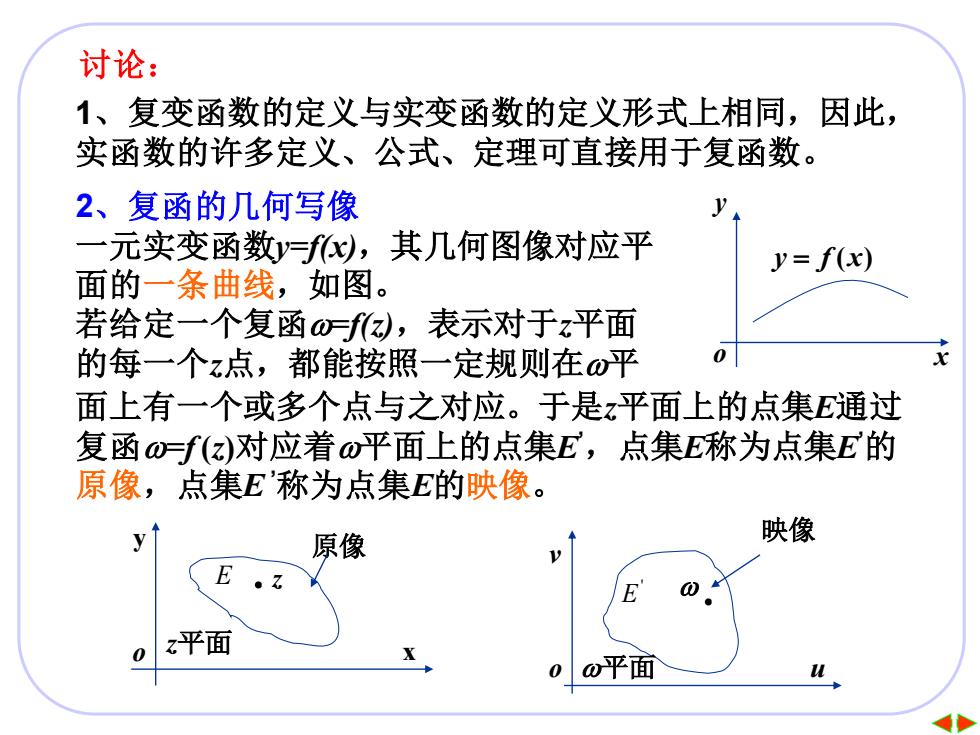
讨论： 1、复变函数的定义与实变函数的定义形式上相同，因此， 实函数的许多定义、公式、定理可直接用于复函数。 2、复函的几何写像 一元实变函数y=fx),其几何图像对应平 y=f(x) 面的一条曲线，如图。 若给定一个复函f,表示对于z平面 的每一个z点，都能按照一定规则在0平 0 面上有一个或多个点与之对应。于是z平面上的点集E通过 复函0f(z)对应着o平面上的点集E,点集E称为点集E的 原像，点集E称为点集E的映像。 y 原像 映像 0 平面 平面 25 讨论： 1、复变函数的定义与实变函数的定义形式上相同，因此， 实函数的许多定义、公式、定理可直接用于复函数。 2、复函的几何写像 一元实变函数y=f(x)，其几何图像对应平 面的一条曲线，如图。 若给定一个复函=f(z)，表示对于z平面 的每一个z点，都能按照一定规则在平 面上有一个或多个点与之对应。于是z平面上的点集E通过 复函=f (z)对应着平面上的点集E’，点集E称为点集E’的 原像，点集E ’称为点集E的映像。 y f x = ( ) x y o 映像 z z平面 x y 原像 o  平面 v o u E ' E