
《数学物理方法》是物理系、电子系本科各专业学生必 修的重要基础课,是在“高等数学”课程基础上的又一重要 的基础数学课程,它将为进行下一步的专业课程学习提供基 础的数学处理工具。所以,本课程受到物理系学生和老师的 重视。 对一个物理问题的处理,通常需要三个步骤:一、利用 物理定律将物理问题翻译成数学问题;二、解该数学问题; 三、将所得的数学结果翻译成物理,即讨论所得结果的物理 意义。因此,物理是以数学为语言的,而“数学物理方法” 正是联系高等数学与物理、电子专业课程的重要桥梁。本课 程的重要任务就是教会学生如何把各种物理问题翻译成数学 的定解问题,并掌握求解定解问题的多种方法,如分离变数 法、付里叶级数法、幂级数解法、积分变换法、保角变换法、 格林函数法、电像法等等
1 《数学物理方法》是物理系、电子系本科各专业学生必 修的重要基础课,是在“高等数学”课程基础上的又一重要 的基础数学课程,它将为进行下一步的专业课程学习提供基 础的数学处理工具。所以,本课程受到物理系学生和老师的 重视。 对一个物理问题的处理,通常需要三个步骤:一、利用 物理定律将物理问题翻译成数学问题;二、解该数学问题; 三、将所得的数学结果翻译成物理,即讨论所得结果的物理 意义。因此,物理是以数学为语言的,而“数学物理方法” 正是联系高等数学与物理、电子专业课程的重要桥梁。本课 程的重要任务就是教会学生如何把各种物理问题翻译成数学 的定解问题,并掌握求解定解问题的多种方法,如分离变数 法、付里叶级数法、幂级数解法、积分变换法、保角变换法、 格林函数法、电像法等等

数学物理方法既可以作为一门纯数 学学科来研究,也可以作为一门应 用数学学科来研究,对工科学生来 说,该课程是作为后续课程的工具 ,学习的目的是应用,因此理论将 尽量少讲
2 数学物理方法既可以作为一门纯数 学学科来研究,也可以作为一门应 用数学学科来研究,对工科学生来 说,该课程是作为后续课程的工具 ,学习的目的是应用,因此理论将 尽量少讲

数学物理方法的主要内容 第一部分:复变函数论及其应用 第一章复变函数 第二章复变函数的积分 第三章幂级数展开 第四章留数定理及其应用 第五章拉普拉斯变换 第六章傅立叶展开
3 数学物理方法的主要内容 第一部分:复变函数论及其应用 第一章 复变函数 第二章 复变函数的积分 第三章 幂级数展开 第四章 留数定理及其应用 第五章 拉普拉斯变换 第六章 傅立叶展开

第二部分数学物理方程及特殊函数论 第七章数学物理方程的定解问题 第八章分离变量法 第九章傅立叶积分法 第十章线性常微分方程的级数解法 第十一章球函数 第十二章柱函数
4 第二部分数学物理方程及特殊函数论 第七章 数学物理方程的定解问题 第八章 分离变量法 第九章 傅立叶积分法 第十章 线性常微分方程的级数解法 第十一章 球函数 第十二章 柱函数

第一章复变函数 §1.1复数 ·§1.2复变函数 ·§1.3解析函数 ·§1.4多值函数 ·§1.5平面向量场复势
5 第一章 复变函数 • §1.1 复数 • §1.2 复变函数 • §1.3 解析函数 • §1.4 多值函数 • §1.5 平面向量场 复势

§1.1复数 数的扩张(完善化) 加法运算:在自然数域N中进行.逆运算(减)出现了零和 负数.自然数域扩大到整数域☑ 乘法运算:在整数域☑中进行.逆运算(除)出现了分数 (有限小数和无限循环小数),整数域扩大到有理数域Q。 乘方运算:在有理数域中进行.逆运算(开方) 出现无理 数(无限不循环小数)和纯虚数。 比乘方的开方逆运算更复杂的逆运算,如解一元二次方程, 将出现复数,数域扩大到复数域。 复数: Z=a+ib (,b为实数) i=√-l 一虚单位 显然: 2=-1,=-i,i4=1
6 数的扩张(完善化) § 1.1 复 数 加法运算:在自然数域N中进行. 逆运算(减)出现了零和 负数. 自然数域扩大到整数域Z. 乘法运算:在整数域Z中进行. 逆运算(除) 出现了分数 (有限小数和无限循环小数),整数域扩大到有理数域Q。 乘方运算:在有理数域中进行. 逆运算(开方) 出现无理 数(无限不循环小数)和纯虚数。 比乘方的开方逆运算更复杂的逆运算,如解一元二次方程, 将出现复数,数域扩大到复数域。 复数: Z a ib = + (a, b为实数) i = −1 -虚单位 显然: 2 3 4 i i i i = − = − = 1, , 1

一、复数的表示法 1、在平面坐标系中 x轴为实轴,单位为1;y轴为虚轴,单 位为i. 代数式:=x+i水.x为z的实部,记为Rz, y为z的虚部,记为Im 显然,一个复数与复平面上一个点有着 一一对应的关系。 2、在极坐标中 x轴为极轴,x、y看成矢量z的直角分量,矢量长度为,与极 轴正方向的夹角为p. 三角式:z=rcosp-+irsinp=r(cosp+isinp)
7 一、复数的表示法 1、在平面坐标系中 x轴为实轴,单位为1;y轴为虚轴,单 位为i. 代数式:z=x+iy. x为z的实部,记为Rez, y为z的虚部,记为Imz. 显然,一个复数与复平面上一个点有着 一一对应的关系。 2、在极坐标中 x轴为极轴,x、y看成矢量z的直角分量,矢量长度为r,与极 轴正方向的夹角为. 三角式: z r ir r i = + = + cos sin (cos sin )

根据欧拉关系: ei=cos+ising. e-io=coso-ising. t=reig 指数式 问题:欧拉关系为什么成立? 如果注意高数中的泰勒展开就知道。 e-r n=0n 心-会aor22-ro-会24nrpm =cos⑩+isino
8 根据欧拉关系: cos sin . cos sin . i i e i e i − = + = − i z re = 指数式 问题:欧拉关系为什么成立? 如果注意高数中的泰勒展开就知道。 0 2 2 1 0 0 0 1 ! 1 1 1 ( ) ( 1) ( 1) ! (2 )! (2 1)! cos sin x n n i n n n n n n n n e x n e i i n n n i = + = = = = = = − + − + = +

根据欧拉关系: ei=coso+ising. e-io coso-ising. =reφ 指数式 欧拉关系也可写成 cosp-() (e-ee) 1 矢量x的长度r称为复数z的模,记为Iz非r=√x+y2 矢量z与极轴正方向的夹角p称为复数的幅角,记为Agz.对于 同一矢量z,其幅角可以相差2kπ,即Argz=P+2kπ 通常规定-Kp≤π为复数x幅角的主值,记为argz.(也有的规 定0Kφ≤2π为幅角主值) argz=p=rcg之,(-π<p≤π)
9 根据欧拉关系: cos sin . cos sin . i i e i e i − = + = − i z re = 指数式 欧拉关系也可写成 1 cos ( ), 2 1 sin ( ). 2 i i i i e e e e i − − = + = − 矢量z的长度r称为复数z的模,记为|z|. 2 2 | | z r x y = = + 矢量z与极轴正方向的夹角称为复数的幅角,记为Argz. 对于 同一矢量z,其幅角可以相差2k,即= Argz= 0+ 2k 通常规定-< 0 为复数z幅角的主值,记为argz. (也有的规 定0< 02 为幅角主值) 0 0 arg , ( ) y z arctg x = = −
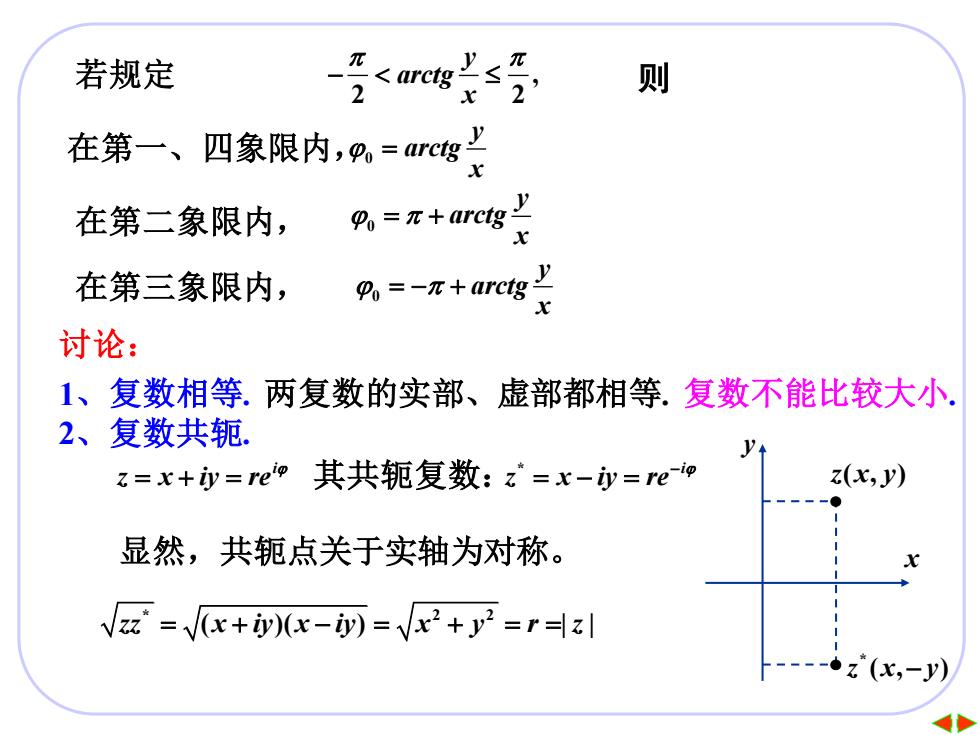
若规定 π 2 则 在第一、 四象限内,风=mg士 在第二象限内, P=+arctg 在第三象限内, 9=-+arctg 讨论: 1、复数相等.两复数的实部、虚部都相等.复数不能比较大小. 2、复数共轭. z=x+y=rep其共轭复数:z=x-y=rep (x,y) 显然,共轭点关于实轴为对称。 √2z=√x+y(x-i)=Vx2+y2=rz -·z(x,-y)
10 若规定 , 2 2 y arctg x − 在第一、四象限内, 0 y arctg x = 在第二象限内, 0 y arctg x = + 在第三象限内, 0 y arctg x = − + 讨论: 1、复数相等. 两复数的实部、虚部都相等. 复数不能比较大小. 2、复数共轭. i z x iy re = + = 其共轭复数: * i z x iy re− = − = • • z x y ( , ) * z x y ( , ) − x y 显然,共轭点关于实轴为对称。 * 2 2 zz x iy x iy x y r z = + − = + = = ( )( ) | | 则