
第一章晶体结构 1.1原子的刚期性排列 Calc以e(CaCO)品体由球形离子组成 固体:品体与非品(玻璃 。 品体由球形高子组成 有序排列的原子 无序排列 Robert Hooke,London 1745 吸引(力和样斥力之间的克争。 便排列导能系统产能量 复杂性!一本以预测材料的陆胸 nttp:/www.rockhounds.com/rockshop/xta 1.1.1品格平移失量 ©重要性:结构在决定因体的物座性质方面起主导作用 点阵(格子)+基元 尚膏定X时钱和中了教射是前定品体结构的主要工具(手段) 也可以用象SEM.TEM,STM,AFM.等微扫描技术(表面 。点阵一空问中的数学点 7=7+u1a1+u2a2+ua3 缺路(Defects) 声子(Phonons)-格子振动 “山,山∈整数 1 a,a2,a=初基矢
1 黄春晖 编著 1 第一章 晶体结构 http://www.rockhounds.com/rockshop/xtal Peruvian Pyrite Drusy Quartz in Geode Tabular Orthoclase Feldspar Encrusting Smithsonite 黄春晖 编著 2 Beltsville 农业研究中心 雪花晶体 黄春晖 编著 3 固体 : 晶体与非晶(玻璃) 有序排列的 原子 无序排列 吸引 (束缚) 力 和 排斥力之间的竞争. 规则排列降低系统的能量. 复杂性 ! - 难以预测材料的结构 1.1 原子的周期性排列 黄春晖 编著 4 ☺ 重要性 : 结构在决定固体的物理性质方面起主导作用 ☺ 确定 : X-射线和 中子散射是确定晶体结构的主要工具(手段). (体) 也可以用象SEM, TEM, STM, AFM. 等微扫描技术(表面) ☺ 衍生 : 存在着非完整晶体. 许多关键的性质依赖于衍生. 缺陷(Defects) –晶体中的非完整性 声子(Phonons) – 格子振动 黄春晖 编著 5 晶体由球形离子组成. Robert Hooke, London 1745 Calcite(CaCO3) 晶体由球形离子组成. Christiaan Huygen, Leiden 1690 由René Haüy预言, Paris, 1822 黄春晖 编著 6 晶体 原子的周期性排列 : 点阵(格子) + 基元 z 点阵 –空间中的数学点 初基矢 整数 = ∈ ′ = + + + 1 2 3 1 2 3 1 1 2 2 3 3 a ,a ,a u ,u ,u r r u a u a u a r 2 a r 1 a r 1.1.1 晶格平移矢量

初始格子胞 12品格的基本类型 Bravais格子的基本分类 斜格平 ·二个货的格干花择书充满整个空风: 单制 对称元来 @厚甲型一一个格点 基于对称性: ©基元与一个原相关一一个初基单元 ©不陆一 )移一如平移一个关量后重合。 ● T=u3+u2a:+ua; Aau=点xa =sind 3度y1204 6度by60 g Centered Rectangular格子a,:23,co4 对称元来 所有的原御同 3)校面对称-如果通过一个李西作反映后重合 均匀质量帝度 Wigner-Sei原抛-廉填鱼中 o 密 2D(伎30的Wigner-Se收更胞 五二维Bravais格子 六为格子☐a44e0 正方格子a90 对称元来 对称元来 ©题小的封闭而积武幻 口密 威 矩形格子 a90 对称元来 ·二度di ▲三度结他i ■四度结etad 镜线(Mro
2 黄春晖 编著 7 2 维s 初始格子胞 • 一个胞通过重复的适当的晶格平移 操作将充满整个空间. - - 一个体积最小的胞. ⊗.每个原胞一一个格点. ⊗.基元与一个原胞相关 - 一个初基单元 ⊗.不唯一 . Wigner-Seitz 原胞 - 格点位于其中心 最高对称性的胞 2 a r 1 a r a a sinφ A a a 1 2 cell 1 2 r r r r = = × 所有的原胞相同 均匀质量密度 黄春晖 编著 8 2 D Oblique 格子 2D (或 3D)的 Wigner-Seitz 原胞 ⊗ 画 一个给定格子点到所有邻近格子点的连线. ⊗. 画连线的垂直平分线 (或 平面). ⊗. 最小的封闭面积 (或 体积) . 黄春晖 编著 9 Bravais 格子的基本分类 基于对称性 : 1) 平移 – 如果平移一个矢量后重合。 2) 旋转 – 如果格子某个轴转动一定角度后重合。 2-度 by 180o 4-度 by 90o 3-度 by 120o 6-度 by 60o 3) 镜面对称 –如果通过一个平面作反映后重合 4) 反演对称 –如果通过一个点作反映后重合 (等同于 旋转 180o 和镜面 ⊥ 旋转轴 r → -r 1 1 2 2 3 3 T = u a + u a + u a 1.2 晶格的基本类型 黄春晖 编著 10 五二维Bravais 格子 正方格子 a1=a2, φ=90o 矩形格子 a1≠a2, φ=90o 单 胞 对称元素 单 胞 对称元素 1 a r 2 a r φ 黄春晖 编著 11 斜格子 a1≠ a2, φ≠60o,90o Centered Rectangular 格子 对称 元素 对称 元素 单 胞 单 胞 a1= 2a2cosφ φ 1 a r 2 a r 黄春晖 编著 12 六角格子 a1=a2, φ=60o 单 胞 对称元素 二度 轴 (dia) 三度 轴 (triad) 四度 轴 (tetrad) 六度 轴 (hexad) 镜线(Mirror)
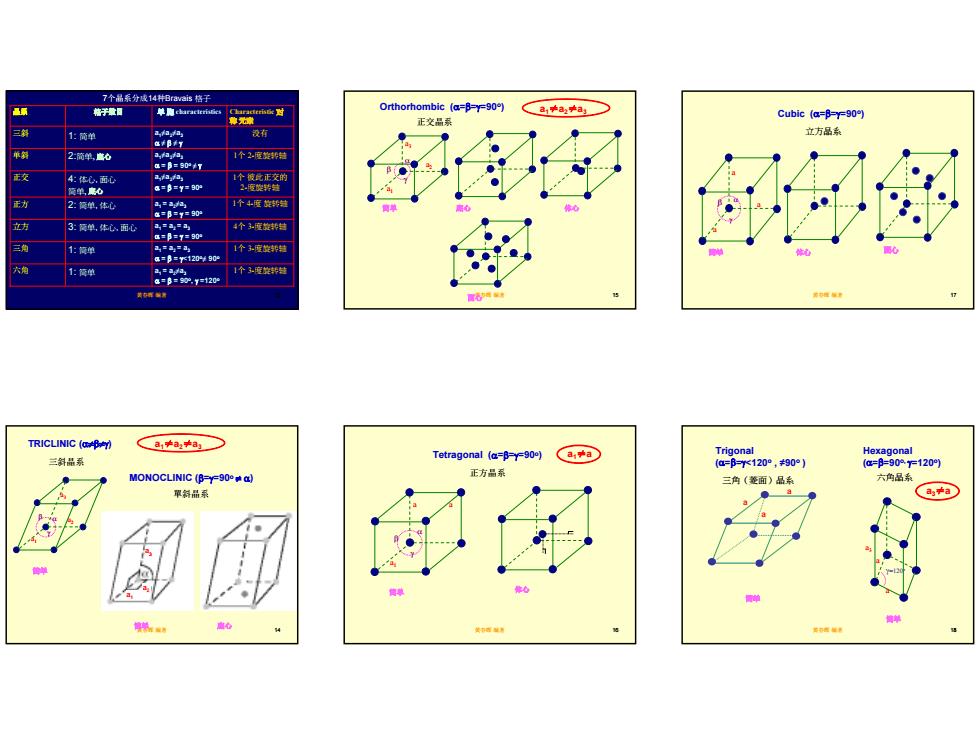
7个品系分成14#Bravais格于 Orthorhombic (a=B-90)a,a2a Cubic (a=B-y=90) 正交品系 南 1:简单 设有 立方品系 2:商单, a==07 4:体,面 能单,0 2:单,体配 1个4座旋新想 90 立方 3:茂单,体心,面配 1个3度旋 a==Y12090 1:营单 1个3度旋# TRICLINIC aa Tetragonal (a=B-y=90)a,a Trigonal Hexagonal 三斜品系 (a=-r1200,¥90°) (@==90mF120) 正方品系 三角(整面)品系 六内品系 郓斜品系 a
3 黄春晖 编著 13 7个晶系分成14种Bravais 格子 a1 = a2≠a3 1个 3-度旋转轴 α = β = 90o, γ =120o 六角 1: 简单 a1 = a2 = a3 1个 3-度旋转轴 α = β = γ<120o≠ 90o 三角 1: 简单 a1 = a2 = a3 4个 3-度旋转轴 α = β = γ = 90o 立方 3: 简单, 体心, 面心 a1 = a2≠a3 1个 4-度 旋转轴 α = β = γ = 90o 正方 2: 简单, 体心 1个 彼此正交的 2-度旋转轴 a1≠a2≠a3 α = β = γ = 90o 4: 体心, 面心 简单, 底心 正交 a1≠a2≠a3 1个 2-度旋转轴 α = β = 90o ≠ γ 单斜 2:简单, 底心 a1≠a2≠a3 没有 α ≠ β ≠ γ 三斜 1: 简单 Characteristic 对 称 元素 晶系 格子数目 单 胞 characteristics 黄春晖 编著 14 a1 a2 a3 α γ β TRICLINIC (α≠β≠γ) MONOCLINIC (β=γ=90o ≠ α) 简单 简单 底心 a1 a3 a2 a1≠a2≠a3 三斜晶系 單斜晶系 黄春晖 编著 15 Orthorhombic (α=β=γ=90o) 简单 底心 体心 面心 a1 a2 a3 α γ β 正交晶系 a1≠a2≠a3 黄春晖 编著 16 a a1 a α γ β Tetragonal (α=β=γ=90o) 简单 体心 正方晶系 a1≠a 黄春晖 编著 17 a a a α γ β Cubic (α=β=γ=90o) 简单 体心 面心 立方晶系 黄春晖 编著 18 a a a3 γ=120o Hexagonal (α=β=90o, γ=120o) Trigonal (α=β=γ<120o , ≠90o ) 简单 简单 三角(菱面)晶系 六角晶系 a a a a3≠a

立方格子的特征 13出面指数系统 对于元具有多个子,引人新的对将 品体中的方向积面 荷单 体心 面心 ·点肝对称 用于开发一种描述品体中品列方向和等阿原子面(品而 格点胞 1 2 4 考您由马,马,可定义的格子 最近原子数 6 8 12 矢量:u,同+u+ud表不为4 最正邻距离 0 其中叫,马和山是最小的互质整数 ·空间点群对 车移使其双回结构 注意 积率 6024 =0.680 ·860片430相同 8 6父 =0.740 ·用代着u列 象大,大福调 披对的件有在许多可能的旋,但大多数无注被观家 山u2以与笛卡尔坐标方向不问,简立方品体除外: 控用佐的形成能量,实标生构遂少数凡个类 品体一原子的周期性排列 立方具有最高的对移方向 10010 空间中拌列的 2姓中5英 3推一14 > 得世 品体项能有等同于减者少千原如Ba达格于的对特性 年。 ●。●● 由对称性得知:【1001[0101【001]是等价的 对称4mm 。惠。 Iī00,0ī0,[00T1 ●。●。 存号{100)-所有的等同方向
4 黄春晖 编著 19 立方 格子的特征 堆积率 最近邻距离 最近邻原子数 6 8 12 格点/胞 1 2 4 简单 体心 面心 2 a a 2 3 0.524 6 = π 0.680 8 3 π = 0.740 6 2 π = a 最大, 与六角相同 黄春晖 编著 20 Bravais格子 + 基元 的 原子 (空间中排列的点) (原胞内的原子排列) 晶体 –原子的周期性排列 2 维 → 5 类 3 维 → 14 类 按对称性 晶体可能有等同于或者少于原始 Bravais 格子的对称性. 基元 对称 “4mm” 黄春晖 编著 21 对于基元具有多个原子,引入新的对称 : • 点群对称 : 组合旋转, 反演, 反映操作,它们都保持 一 点不动并返回原结构. 2 维 , 10 3 维 , 32 • 空间点群对称 : 点群操作 + 平移使其返回原结构. 2 维 , 17 3 维 , 230 按对称性存在许多可能的类,但大多数无法被观察. 按晶体的形成能量,实际晶体构成少数几个类. 黄春晖 编著 22 黄春晖 编著 23 考虑由 定义的格子 矢量 表示为 [u1 u2 u3] 其中u1, u2, 和 u3 是最小的互质整数. 1 2 3 a , a , a 晶体中的方向和平面 用于开发一种描述晶体中晶列方向 和 等同原子面(晶面) 1 1 2 2 3 3 r = u a + u a + u a r 注意 : • [8 6 0]与 [4 3 0]相同 • 用ū代替 -u • [u1 u2 u3] 与笛卡尔坐标方向不同,简立方晶体除外。 [121] 1.3 晶面指数系统 黄春晖 编著 24 由对称性得知, [ 1 0 0 ], [ 0 1 0 ], [ 0 0 1 ]是等价的 [ 1 1 0 ] [ 1 1 1 ] [ 1 0 0 ] [ 0 0 1 ] [ 0 1 0 ] 立方具有最高的对称方向 [ 1 0 0 ],[ 0 1 0 ],[ 0 0 1 ] 符号 { 1 0 0 } ≡ 所有的等同方向
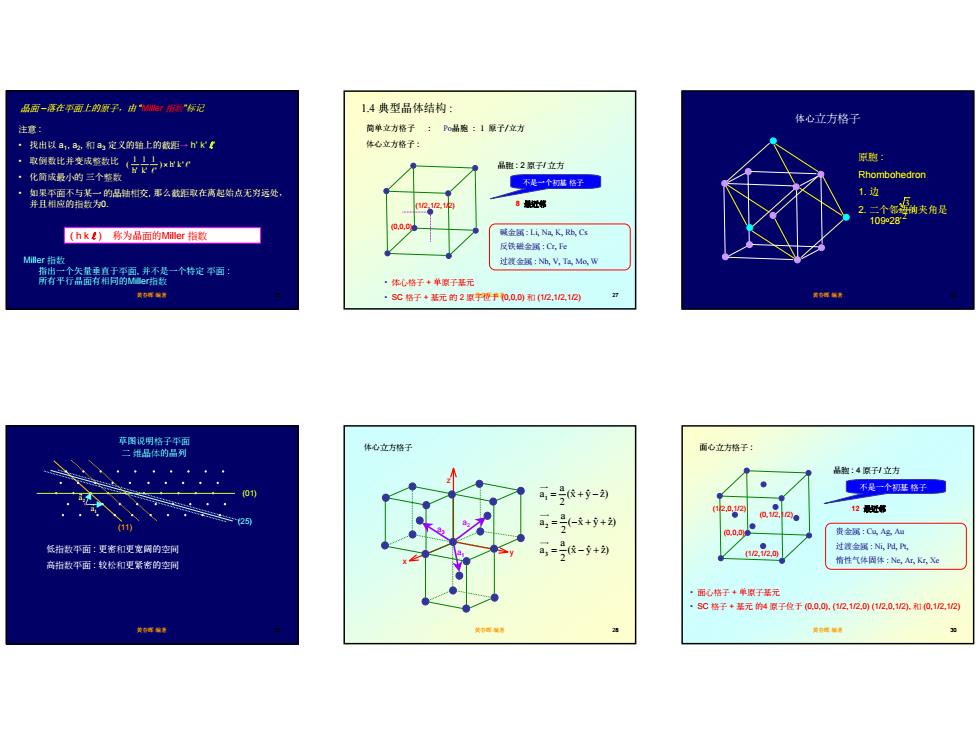
品面-落在季面上的原子,由台帝你记 1.4典型品体结构: 体心立方格子 注意: 简单立方格子:0品胞:1原子/位力 ·找出以a1,2,和ay定义的鞘上的截图一hK( 体心立方格子: 。取倒数比并变成整数比(付之( 原跑 品跑:2数子刊立方 ·化面成最小的三个整数 不是一个感格子 Rhombohedron 1边 8u球 源夹是 (hk)称为品面的Mer指数 金通:L山Na K,Rb,Cs 反铁班金属:C,e Mer指数 过属:Nh,V,面MaW 转学在疆精惠井餐一个特定酒 ,体儿格子+单子基元 ·SC格子+基元的2取宇橙于和,0,0和(12.121回 体心立方格于 而心立方格子 品跑:4原子刊立方 01 耳=依+9-刻 不是一个视座格子 12处常 11 25 =-+5+2刘 贵金属:CLA文如 气指救平面:更老和更宽阀的空间 -+ (V2.V2.) 过装金国:N,H,气 高指数平面:较松和更紧瓷的空可 情性气固体:N,A,K,X 面格子+单原子基元 sC格子+基元的4原子位于0.0,0.(12,12.0(12.0,12.和0,1212
5 黄春晖 编著 25 晶面 –落在平面上的原子,由 “Miller 指数”标记 注意 : • 找出以 a1, a2, 和 a3 定义的轴上的截距→ h’ k’ l’ • 取倒数比并变成整数比 • 化简成最小的 三个整数 • 如果平面不与某一 的晶轴相交, 那么截距取在离起始点无穷远处, 并且相应的指数为0. ) h' k ' ' ' 1 k' 1 h' 1 ( l l × Miller 指数 指出一个矢量垂直于平面, 并不是一个特定 平面 : 所有平行晶面有相同的Miller指数 ( h k l ) 称为晶面的Miller 指数 黄春晖 编著 26 (11) (01) (25) 草图说明格子平面 二 维晶体的晶列 低指数平面 : 更密和更宽阔的空间 高指数平面 : 较松和更紧密的空间 2 a r 1 a r 黄春晖 编著 27 1.4 典型晶体结构 : 体心立方格子 : 晶胞 : 2 原子/ 立方 不是一个初基 格子 8 最近邻 碱金属 : Li, Na, K, Rb, Cs 反铁磁金属 : Cr, Fe 过渡金属 : Nb, V, Ta, Mo, W (0,0,0) (1/2,1/2,1/2) • 体心格子 + 单原子基元 • SC 格子 + 基元 的 2 原子位于 (0,0,0) 和 (1/2,1/2,1/2) 简单立方格子 : Po晶胞 : 1 原子/立方 黄春晖 编著 28 x z a1 y a2 a3 (xˆ yˆ zˆ) 2a a ( xˆ yˆ zˆ) 2a a (xˆ yˆ zˆ) 2a a 3 2 1 = − + = − + + = + − 体心立方格子 黄春晖 编著 29 体心立方格子 原胞 : Rhombohedron 1. 边 2. 二个邻边的夹角是 109o28’ a 2 3 黄春晖 编著 30 面心立方格子 : 晶胞 : 4 原子/ 立方 不是一个初基 格子 12 最近邻 贵金属 : Cu, Ag, Au 过渡金属 : Ni, Pd, Pt, 惰性气体固体 : Ne, Ar, Kr, Xe • 面心格子 + 单原子基元 • SC 格子 + 基元 的4 原子位于 (0,0,0), (1/2,1/2,0) (1/2,0,1/2), 和 (0,1/2,1/2) (0,0,0) (1/2,1/2,0) (1/2,0,1/2) (0,1/2,1/2)
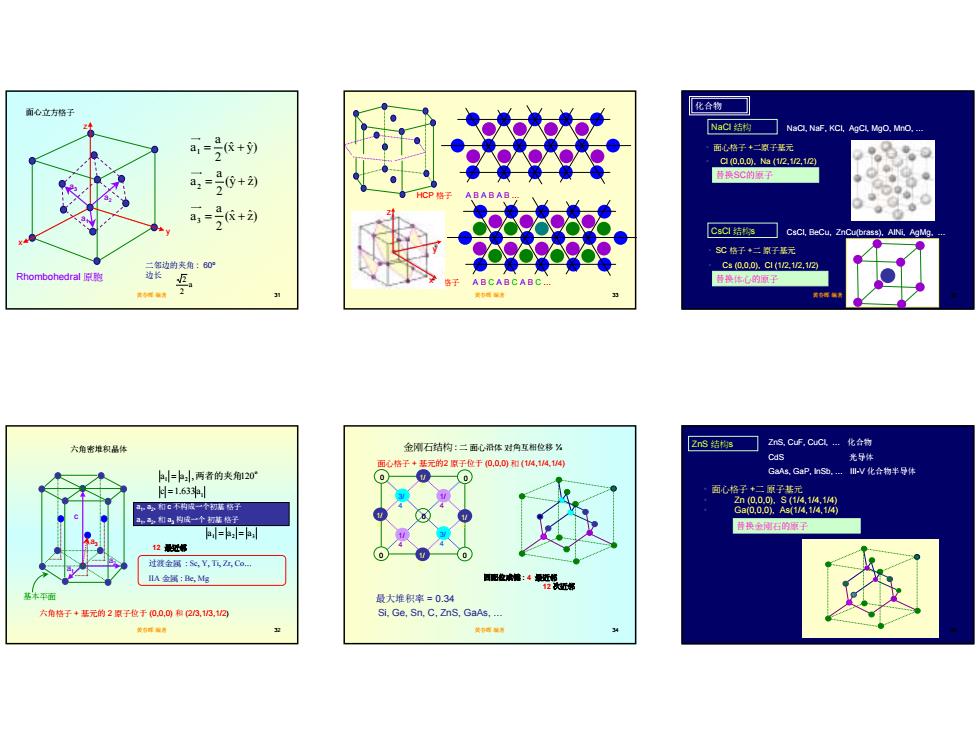
面心立方格子 化合特 NaC结物☐NaC.Naf.KCI,AgCL Mgo.Mino. a=2+y 面,格子+二源于元 c0,0.0.s12.,12,12 马-0+刘 音换SC的原子 画,-+习 0 SC格子+二蒙子基元 C0.00,C(212.12 Rhombohedral原e ABCA日CAB 普换体心的原子 六角密堆积品体 金隔石结构:二面心沿体角互相位移 2ns结s☐Zns.c.Cuc-化合物 Cas 光导体 =:,两者的夹20 哥于如手aa0和Ak4 GaAg.GaR,hs.-m-V化合物半休 =1.63 面心格子+二原子基元 和不利成一个初格子 &a88A ,和构成一个基格子 pl=2= 普换金南石的原子 2最处第 过额金:Sc,Y,TZ红,Co A金满:,Mg 泥包:4s 大堆积=034 大角格子+基元的2傲子位于0,0,0和23,18,松 Si.Ge,Sn,C,ZnS,GaAs
6 黄春晖 编著 31 面心立方格子 x y z a1 a2 a3 (xˆ zˆ) 2a a (yˆ zˆ) 2a a (xˆ yˆ) 2a a 3 2 1 = + = + = + Rhombohedral 原胞 二邻边的夹角 : 60o 边长 a 2 2 黄春晖 编著 32 六角密堆积晶体 a1 a2 c 基本平面 a1, a2, 和 c 不构成一个初基 格子 a1, a2, 和 a3 构成一个 初基 格子 六角格子 + 基元的 2 原子位于 (0,0,0) 和 (2/3,1/3,1/2) 过渡金属 : Sc, Y, Ti, Zr, Co. IIA 金属 : Be, Mg c 1.633a a a , 120 1 o 1 2 = = 两者的夹角 12 最近邻 a3 a a a 1 = 2 = 3 黄春晖 编著 33 HCP 格子 A B A B A B . 面心格子 x A B C A B C A B C . y z 黄春晖 编著 34 0 0 0 0 0 1/ 2 1/ 2 1/ 2 1/ 2 1/ 4 1/ 4 3/ 4 3/ 4 金刚石结构 : 二 面心沿体 对角互相位移 ¼ 最大堆积率 = 0.34 Si, Ge, Sn, C, ZnS, GaAs, . 面心格子 + 基元的2 原子位于 (0,0,0) 和 (1/4,1/4,1/4) 四配位成键 : 4 最近邻 12 次近邻 黄春晖 编著 35 化合物 NaCl 结构 NaCl, NaF, KCl, AgCl, MgO, MnO, . • 面心格子 +二原子基元 • Cl (0,0,0), Na (1/2,1/2,1/2) CsCl 结构s CsCl, BeCu, ZnCu(brass), AlNi, AgMg, . • SC 格子 +二 原子基元 • Cs (0,0,0), Cl (1/2,1/2,1/2) 替换SC的原子 替换体心的原子 黄春晖 编著 36 ZnS 结构s ZnS, CuF, CuCl, . 化合物 CdS 光导体 GaAs, GaP, InSb, . III-V 化合物半导体 • 面心格子 +二 原子基元 • Zn (0,0,0), S (1/4,1/4,1/4) • Ga(0,0,0), As(1/4,1/4,1/4) 替换金刚石的原子

High Tc超导体 1.6非理想品体结构 Zmc Fkande 动e4详n区 tndert内iny tattioe is hep 许多品体结构随T,P改变: 例如 0 S-femte a-ferite Fe 910-C 1400 210C HCP Na 371K Orthorhombic Tetragonal Orthorhombic O(l)(Pmmm) T(P4/mmm) O(l)(Cmmm) 菌精丝 第博 1.5原子结构的直接成视 C-60 某些原子形成爹种稳定结构 例如,C一金刚石或石是(大角】 "Bucky balls" BuckminsterFullurene 幅STM成像的的石题表面,清楚地 显示石墨六图环的相互连接情况
7 黄春晖 编著 37 a b c Orthorhombic O(I) (Pmmm) O(3) Cu(2) Cu(1) O(1) Ba/Pr Pr O(4) O(2) O(5) Tetragonal T (P4/mmm) Ba/Pr Pr O(2) O(1) O(3) Cu(2) Cu(1) Ba/Pr Pr O(2) O(1) Cu(2) Cu(1) O(3) Orthorhombic O(II) (Cmmm) High Tc 超导体 黄春晖 编著 38 C-60 “Bucky balls” BuckminsterFullurene 黄春晖 编著 39 黄春晖 编著 40 某些原子形成多种稳定结构: 例如, C → 金刚石 或 石墨 (六角) 一幅STM成像的的石墨表面,清楚地 显示石墨六圆环的相互连接情况 1.5 原子结构的直接成像 黄春晖 编著 41 许多晶体结构随T, P改变: 例如, Fe 温度 910oC 1400oC 2100oC 体心 面心 体心 液体 Na 温度 36K 371K HCP 面心 液体 δ-ferrite α-ferrite 1.6 非理想晶体结构