
第三章 幂级数展开 §3.1复数项级数(数值级数) 定义复数级数山+4+山2+.+un+.= n=0 令un的实部和虚部分别为on与Bn,则 u-+24 个复数级数∑4n完全等价于两个实级数∑an和∑pn, 级数的收敛与发散 如果级数部分和Sn=u+4+山2+.+un 如果imSn存在,即imSn=S,则称复数项级数收敛,S 称为级数的和{Sn}的极限: 如果mS不存在或趋于无穷,则复数项级数发散
11 第三章 幂级数展开 §3.1 复数项级数(数值级数) 令un的实部和虚部分别为n与n,则 一个复数级数 un 完全等价于两个实级数 n 和 n , 级数的收敛与发散 定义 复数级数 0 1 2 0 n n n u u u u u = + + + + + = 0 0 0 n n n n n n u i = = = = + n n 0 1 2 如果级数部分和 S u u u u = + + + + 称为级数的和 的极限; lim n n S S → lim n = n S → Sn 如果 存在,即 ,则称复数项级数收敛,S lim n n S 如果 → 不存在或趋于无穷,则复数项级数发散

-δ定义对于任意给定的ε>0,存在N =N(e),使得当n≥N时,有lSnS<8, 则复数项级数收敛 几何意义:当n≥N时所有都落在在以S为 S V+2 圆心以e为半径的圆内.也就是说当n≥N +1 时所有的Sm都聚集在S点的邻域内. 绝对收敛 若24收敛,则称级数24,为绝对收敛级数。 绝对收敛的级数一定是收敛的,反之,一个收敛的级数不一 定是绝对收敛的。 |un+1+n+2+.+un+plun+1+|un+2|+.+|un+p 级数收敛的判断法 必要条件:若∑4。收敛.则4。=0;若四≠0,则 24.发散
22 -定义 对于任意给定的 > 0,存在N = N( ),使得当n N时,有|Sn –S|< , 则复数项级数收敛. S SN SN+1 几何意义:当 SN +2 n N时所有都落在在以S为 圆心以为半径的圆内. 也就是说当n N 时所有的Sn都聚集在S点的邻域内. 绝对收敛 若 收敛,则称级数 为绝对收敛级数. 0 k k u = 0 | | k k u = 绝对收敛的级数一定是收敛的,反之,一个收敛的级数不一 定是绝对收敛的。 1 2 1 2 | | | | | | | | n n n p n n n p u u u u u u + + + + + + + + + + + + 级数收敛的判断法 必要条件:若 收敛. 则 ;若 ,则 0 k k u = lim 0 n n u → = lim 0 n n u → 发散. 0 k k u =

证明: 若级数∑4收敛,有 k-0 limS=S,lim S-1=S,◆ lim(S,-S-1)=0. 100 l→a0 即:imwn=0 1-yc0 充要条件(科希收敛判据): 对任给e>0,存在N=Nel,使得当n≥N时,有1岂:Ke (p为任意正整数),则级数收敛. 总结: 1、若∑“收敛,可得到m,=0;反推不成立. 2、若2,绝对收敛,可得到24,:反推不成立。 3
33 证明:若级数 收敛,有 0 k k u = 1 lim , lim , n n n n S S S S − → → = = 1 lim( ) 0. n n n S S − → − = 即: lim 0 n n u → = 充要条件(科希收敛判据): 对任给 >0,存在N = N(),使得当n N时,有 1 | | n p k k n a + = + (p为任意正整数),则级数收敛. 总结: 2、 若 绝对收敛,可得到 ;反推不成立. 0 k k u = 0 k k u = 1、 若 收敛,可得到 lim 0 n ;反推不成立. n u → = 0 k k u =

§3.2 复变项级数(函数级数) 复变项级数 4.(a=4a)+u(a)++,(a+”geG. k 若z点为G内任意一点,则 2么名=,+4G+.+G+p 这时复变项级数退化为复数项级数,可以利用上面方法 来讨论它的收敛性.其部分和为: S()∑4x(亿)=4(亿)+4(亿)+.+4() k0 若imS()=S(z),S(zo)为唯一确定的极限值,则称级数在 z=0收敛。 e-δ说法对于任意给定的ε>0,存在N=N(8,zo),使得当 n≥WN时,有Sn(zo)-Szol<8,则级数收敛. 将上面的zo换成z,则称复变项级数∑4,(a)在z收敛, k=0
44 §3.2 复变项级数(函数级数) 复变项级数 0 1 0 ( ) ( ) ( ) ( ) , ( ). k n k u z u z u z u z z G = = + + + + 若z0点为G内任意一点,则 0 0 0 1 0 0 0 ( ) ( ) ( ) ( ) , k n k u z u z u z u z = = + + + + 这时复变项级数退化为复数项级数,可以利用上面方法 来讨论它的收敛性. 其部分和为: 0 0 0 0 1 0 0 0 ( ) ( ) ( ) ( ) ( ) n n k n k S z u z u z u z u z = = + + + 若 ,S(z0 )为唯一确定的极限值,则称级数在 z = z0收敛。 0 0 lim ( ) ( ) n n S z S z → = -说法 对于任意给定的 > 0,存在N = N(, z0 ),使得当 n N时,有|Sn (z0 ) –S(z0 )| < ,则级数收敛. 将上面的z0换成z,则称复变项级数 在z收敛. 0 ( ) k k u z =

致收敛级数 对于任意给定的ε>0,存在N=N(ε),N 与z无关,使得当n≥N时,有lS(a)-S(z0,存 在N=Ne),使得当n≥N时,有Sn-S<8,即: 0m+1+0n+2+.<E 对于级数立: k=0 .(a-24,a=ue+4a++u,②, S2)白24.@)=u@+W@++0,②+
55 一致收敛级数 对于任意给定的 > 0,存在N = N( ),N 与z无关,使得当n N时,有|Sn (z) –S(z)| 0,存 在N = N( ),使得当n N时,有|Sn–S| < ,即: n n 1 2 a a + + + + 0 k k a = 对于级数 0 k k u = 0 1 0 ( ) ( ) ( ) ( ) ( ), n n k n k S z u z u z u z u z = = = + + + 0 1 0 ( ) ( ) ( ) ( ) ( ) , n k n k S z u z u z u z u z = = = + + + +

|Sn(z)-S(z)月4n+1+un+2+.图un+1+|4+2|+.≤a+1+0n+2+.0,存在N=N(e),使得当n≥N时, 有lSn()-S(0,存在N=N(ε), 使得当m≥N时,之4Ks(p为任意正整数),则级数收敛 k=u+ 致收敛的重要性质: 1、若∑“(②)为G内一致收敛的连续函数项级数,则 ① 级数和S()=∑“,(②)也是G内的连续函数(连续性) 这个性质告诉我们,如果级数的每一项都是连续函数,则一 致收敛的级数可以逐项求极限,也就是说“求极限”和“求 和”可以交换次丽立,@-,6) ② 可以逐项积分,即∫sz)k=∫∑u.(e)k=∫u,(edk
66 1 2 1 2 1 2 | ( ) ( ) | | | | | | | S z S z u u u u a a n n n n n n n − = + + + + + + + + + + + + 有|Sn (z)–S(z)| 0,存在N = N( ),使得当n N时, 0 k k u = 一致收敛的重要性质: 2、科希判据(充要条件)对于任给定的 > 0,存在N = N( ), 1 | | n p k k n a + = + 使得当n N时, (p为任意正整数),则级数收敛. 1、若 为G内一致收敛的连续函数项级数,则 0 ( ) k k u z = ① 级数和 也是G内的连续函数(连续性) 0 ( ) ( ) k k S z u z = = 0 0 ( ) ( ) ( ) . k k k k S z dz u z dz u z dz = = ② 可以逐项积分,即 = = 这个性质告诉我们,如果级数的每一项都是连续函数,则一 致收敛的级数可以逐项求极限,也就是说“求极限”和“求 和”可以交换次序. 1 1 lim ( ) lim ( ) o o k k z z z z k k u z u z → → = = =

2、若∑“,(a)为G内一致收敛的解析函数项级数,则 ①若e)-u,(e在G内的解析函数. 证明:由于k在G内解析,4ka)必连续,其和(a=24,(a) k=0 因此也是G内的连续函数, 如图,飞在1上取值,z为G的内点,故 p(5) (5-z) 在止连续,积分手警5存在 G 1∮525= 4, k=0 -D 2πi915-z 、d5 2πi1(传-z) 2πi105-z 于∑)为一致收敛的连续函数项级数,可逐项积分 1f5=2L∮“15 2ri915-z 02πi15-z 7
77 2、若 为G内一致收敛的解析函数项级数,则 0 ( ) k k u z = ① 若 在G内的解析函数. 0 ( ) ( ) k k z u z = = 证明:由于uk (z)在G内解析,uk (z)必连续,其和 因此也是G内的连续函数. 0 ( ) ( ) k k z u z = = G l z 0 ( ) 1 ( ) 1 2 2 ( ) k k l l u d d i z i z = = − − 如图,在l上取值,z为G的内点,故 ( ) ( )z − 在l上连续,积分 存在 ( ) ( ) l d z − 0 1 ( ) 2 k l k u d i z = = − 0 ( ) k k u z = − 由于 为一致收敛的连续函数项级数,可逐项积分: 0 1 ( ) 1 ( ) 2 2 k l l k u d d i z i z = = − −

由于u()为G内的解析函数,根据科西公式: “()= 2ri915-z 代入上式得:24g-=m】 k=0 上式表明0(z)可表示成边界的线积分,即0(z)为单连 通区G的科西公式,因此,为G内的解析函数。 ② 可逐项微商,即:pa)=立.-立ua 证:由于o(z)为G内的解析函数,根据高阶的科西公式: 24.(5)
88 由于uk (z)为G内的解析函数,根据科西公式: 1 ( ) ( ) 2 k k l u u z d i z = − 代入上式得: 0 1 ( ) ( ) ( ) 2 k l k d u z z i z = = = − 上式表明(z)可表示成边界的线积分,即(z)为单连 通区G的科西公式,因此,为G内的解析函数。 ② 可逐项微商,即: ( ) ( ) ( ) 0 0 ( ) [ ( )] ( ) n n n k k k k z u z u z = = = = 证:由于(z)为G内的解析函数,根据高阶的科西公式: ( ) 0 1 1 1 0 ( ) ! ( ) ! ! ( ) ( ) 222 ( ) ( ) ( ) k n k k n n n lll k u nnn u z d d d iii z z z = + + + = === − − −

由于立,(⑤是一致收敛的连续项函数,尼 也是 致收敛的连续函数,可逐项积分,故: p(a=2455 62πi(传-z)* 由于u()为G内的解析函数,根据高阶导数的科西公式: m(z)=于 n!不(5) 2i作-5 k=0
99 由于 是一致收敛的连续项函数, 也是 0 ( ) k k u = 1 0 ( ) ( ) k n k u z + = − ( ) 1 0 ! ( ) ( ) 2 ( ) n k n l k n u z d i z + = = − 一致收敛的连续函数,可逐项积分,故: 由于uk (z)为G内的解析函数,根据高阶导数的科西公式: ( ) 1 ! ( ) ( ) 2 ( ) n k n l n u u z d i z + = − ( ) ( ) 0 ( ) ( ) n n k k z u z = =
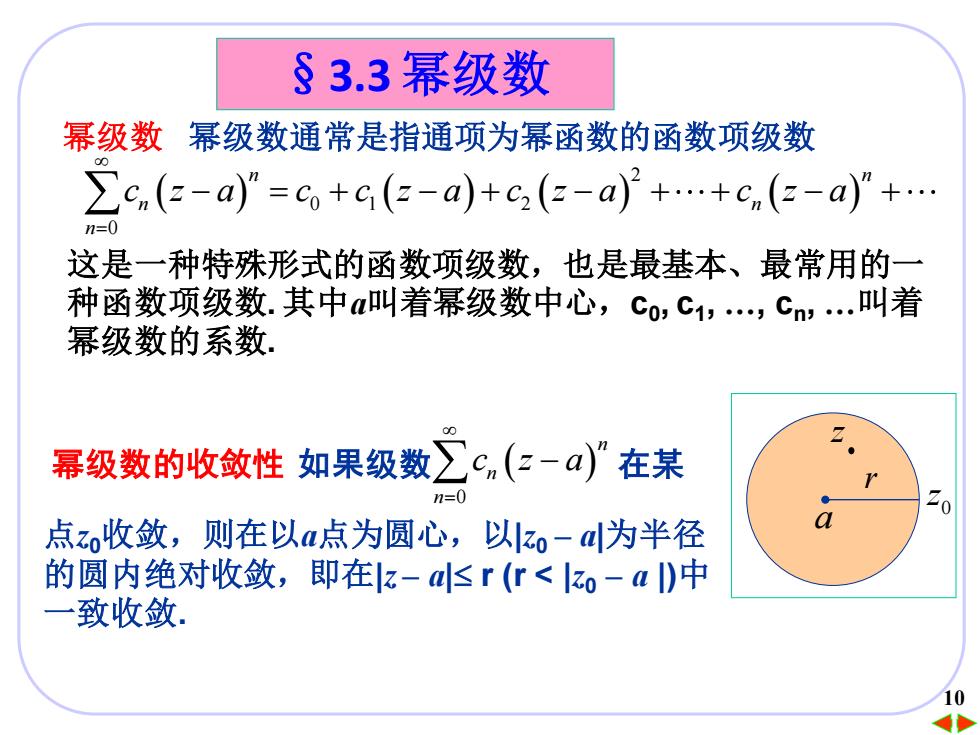
§3.3幂级数 幂级数幂级数通常是指通项为幂函数的函数项级数 6(-a)-ate(-a)+e(-a)t+c(-a)+ 这是一种特殊形式的函数项级数,也是最基本、最常用的一 种函数项级数.其中a叫着幂级数中心,co,c1,cn叫着 幂级数的系数 幂级数的收敛性如果级数∑cn(2-a)”在某 n=0 点zo收敛,则在以a点为圆心,以-d为半径 的圆内绝对收敛,即在z-dsr(r<lo-a)中 致收敛 10
1010 §3.3 幂级数 这是一种特殊形式的函数项级数,也是最基本、最常用的一 种函数项级数. 其中a叫着幂级数中心,c0 , c1 , ., cn , .叫着 幂级数的系数. 幂级数 幂级数通常是指通项为幂函数的函数项级数 ( ) ( ) ( ) ( ) 2 0 1 2 0 n n n n n c z a c c z a c z a c z a = − = + − + − + + − + 点z0收敛,则在以a点为圆心,以|z0 – a|为半径 的圆内绝对收敛,即在|z – a| r (r < |z0 – a |)中 一致收敛. ( ) 0 n n n c z a = 幂级数的收敛性 如果级数 − 在某 z a r 0 z