
第六章自由电子费米气孙 基本观点:推动原子聚集形成品体 品体是金属,绝缘练,或牛导体是由什么决定的? 固体的能带结杓 。0 空态 分子 品 空态 空态 态 价带满 子电带尘 分立的能级 分裂的能圾 能带的态 低能级保持分立并局域在子周围。芯 传好电子是有效的在商温传电 没有传导电子 密能牙习产我的能数构成能荐可以灯提到整个品体限据电子筑充的 在箱体内的自由传导电子 电子没有相互作用 (箱壁除外) 自由电子模型一处理传导电子作为自由粒子 g 连线态一态密瘦 。费米统计一占据态 理型的电子相互作用: 热学性频一热能热容 离子一稳定的库仑相互作用(电子结合),如 电与热传一我号电子的 。受到芯电于的屏敲大距离的吸引减弱 ·磁场效应 。泡利不相容原理要求传导电子处在远裤局城在原子网围的芯电子 电子一强的库仑排示 。库仑排斥·泡利不相容原理 电子顿向于分窝 通常情况下,这样的周期链 U(X)0 05xsL 边界条件 -a山→人= 其它情况 态密度 每个k态的间隔 Ak=2wL 2mΨ+= 2D(k)dk=D(s)de 均匀 %0)=gL)=0 DE)=2Dk进-2U2) d起/dk =Ast.刘即晋和- 和K2m 2m 2mL2 2低 D(s) 泡利不相晾理+自旋简并(每个能级两个自旋幻 电子开始从底部能级一)填充并日维线填充更高的能极,直到全部N电子都 OC 6-12 维的单粒于子自态密度 .,这里n表示被填充的能的最高n
1 1 第六章 自由电子费米气体 晶体是金属, 绝缘体, 或 半导体 是由什么决定的? 固体的能带结构 满 态 空 态 导电 带 部分占满 满 态 空 态 Eg 价 带 满 / Eg>kBT 空 态 满 态 Eg 金属 半导体 绝缘体 传导电子是有效的 在高温或掺杂下,传导电 子是有效的 没有传导电子 E 2 基本观点 : 推动 原子聚集形成晶体 自由 原子 分子 晶体 分立的能级 分裂的能级 能带的态 低能级保持分立并局域在原子周围. 芯态 高能级分裂密集的能级构成能带,可以扩展到整个晶体,根据电子填充的 情况,分为价带和导带 3 自由电子模型 – 处理传导电子作为自由粒子 9 连续态 – 态密度 9 费米统计 – 占据态 9 热学性质 – 热能, 热容量, . 9 电与热传输 –传导电子的散射 9 磁场 效应 4 理想的电子相互作用 : 离子 – 稳定的库仑相互作用 (电子结合),但 z 受到芯电子的屏蔽大距离的吸引减弱 z 泡利不相容原理要求传导电子处在远离局域在原子周围的芯电子. 电子 – 强的库仑排斥 而且 • 库仑排斥 • 泡利不相容原理 电子倾向于分离 电子没有相互作用 (箱壁除外) ( ) 2m k 2m P ε K.E. 2 2 h = = = 在箱体内的自由传导电子 5 0 L x U→ ∞ U(x)= 0 0 ≤ x ≤ L ∞ 其它情况 − Ψ + U(x)Ψ = εΨ dx d 2m 2 2 2 h SchrÖdinger 方程 0 对于一维情况 ( ) ( ) 2 2 2 2 n n n n n 2mL ( nπ ) 2m k ε L nπ Asin k x : k h h ϕ = 即 = 和 = = 边界条件 (0) (L) 0 ϕn =ϕn = 因此, 在一条线里,如何容纳N 电子 ? 泡利不相容原理 + 自旋简并 (每个能级两个自旋↑↓) 电子开始从底部能级(n=1)填充并且继续填充更高的能级,直到全部 N 电子都 容纳. 1,., nF, 这里 nF 表示被填充的能级的最高 n值. 6 通常情况下, 这样的周期链 态密度 每个 k态的间隔 ∆k=2π/L 边界条件 (x) (x L) ϕn =ϕn + L n2π kn = ± 2π L (2π /L) 1 ∆k 1 D(k) n = = = 均匀 dε / dk 2(L/2π ) dε 2D(k)dk D( ε ) 2D(k)dk D(ε )dε = = = 和 ε=h2k2/2m ( ) ε 1 2π mL k 2m 2π mL k/m 2(L/2π ) D( ε ) 2 2 h h h h = = = 一 维的单粒子自旋 态密度 k ε ε D(ε) ∝ ε -1/2

在三性情况下 韩定博方程 ×2自旋容纷 边界条件:平是x¥,和工方向的周期活数其周期为[ 每个k态的体积元k故k=2LP 一x六台尚 0)=(何三准用 电子和声子间的驱别 态k≤,技古邯 费米球-基态电子在空同占据体积 色 D(a)xo? 电子数 达到画 自费米球的体积DW 林态T0,底能极填充:2个个能级 最高古邦能级。 →。 费米能量> 典型地一10cm 、1-10av 最大能量:4:一m o N-D(E)Re)de 国是能量态较占搭的几丰 "t 。 票四2质是风西的电子杏所镜
2 7 在三维情况下, 边界 条件 : Ψ是x, y, 和 z 方向的周期函数, 其周期为 L Ψ + Ψ = Ψ ∂ ∂ + ∂ ∂ + ∂ ∂ − U(x, y,z) ε 2m x y z2 2 2 2 2 2 2 h 薛定谔方程 0 ,. L 4π , L 2π ,. ;k 0, L 4π , L 2π ,. ;k 0, L 4π , L 2π k 0, x = ± ± y = ± ± z = ± ± 每个k态的体积元 ∆kx ∆ky ∆kz=(2π/L)3 ( )3 3 3 x y z 2π V 2π L (2π /L) 1 ∆k ∆k ∆k 1 D(k) = = = = ( ) ( ) ( ) dε 2m ε 4π V dε k m 2π 4π k V dε dε / dk 1 4π k 2π V D( ε )dε D(k)4π k dk 3 3 3 2 2 2 2 3 2 h h = = = = 8 ε 2m 4π V D( ε ) 3/ 2 2 2 = h 三维情况单粒子自旋态密度 x 2 自旋容纳 传导电子 : 自由运动跑遍整个晶体 传导电子密度n = N/V (Table 1) 典型地 n ~ 1022 ~ 1023 cm-3 大多数是 “s” 轨道电子 也有 “p” 和 “d” ε 2m 2π V D( ε ) 3/ 2 2 2 = h 三维态密度 ∝ ε 1/2 D(ε) ε 9 电子 和 声子间的区别 电子 声子 数目 N=nV 固定 N ~ kBT 变化 w/. T 容纳 费米子 玻色子 (费米-狄拉克 统计力学) (Planck 分布) 每个轨道态两个 ↑↓ 每个被激发模n 个 色散 ε ∝ k2 ω ∝ k 态密度 D(ε) ∝ ε 1/2 D(ω) ∝ ω2 达到 ωD 德拜 基 态 T=0,底能级填充 : 2个 /每个能级 ↑↓ εn ε3 ε4 ε1 ε2 εF 最高占据能级 ε F 费米能量 最大能量 : ε F = h2kF 2/2m 10 kx ky kz kF 态 k ≤ kF 被占据 费米球 –基态电子在k-空间占据体积 费米面 – kF 态 w/. ε = εF #电子数 (2π ) V πk 3 4 N 2 3 3 = F = 自旋 费米球的体积 D(k) V 3π N 2m ε V 3π N k 2/3 2 2 F 1/3 2 F = = h 和 典型地, ~ 10-8 cm-1 ~ 1 – 10 eV 11 n εF TF 12 f(ε) ε 0 1 εF εF f(ε) 是能量 ε态 被占据的几率 f(ε)= 1 , ε ≤ εF 0 , ε > εF ∫ ∫ = = ∞ F ε 0 0 D( ε )dε N D( ε )f( ε )dε 费米能量很重要因为电子的性质是只由εF 附近的电子态所决定. kBT << εF { T=0 D(ε) ε
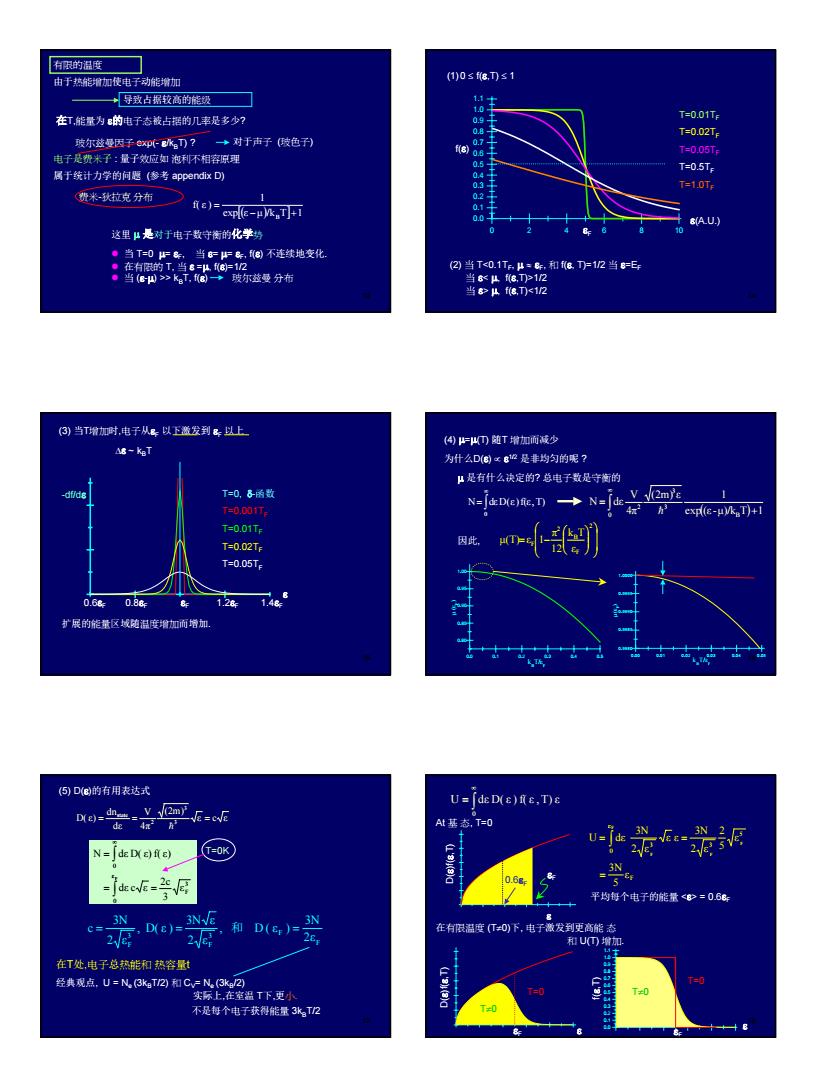
的温度 由于拉增加使电子动能增加 (1))s1 母致占搭牧高的能经 在能量为的电子态古银的几是多少? 你因子初?→对干声子陵色刊 属于线力学的腿考a I-05T, 不球拉克分市>e-中可丽 这里以是对于电子数守衔的化学纷 (③当T瑞加时电子从长以下数发到器以上 句兴D随T带如雨少 A8-keT 为什么DGx62是垂均匀的呢7 :是有什么说定的总电子数是守衡的 Nj4ee,n→N-j T-0.05T 1.48 扩展的量区城地温度增加而增加 (⑤D@的有用表达式 UDc)e,D At基态T=0 平均每个电子的能量<g=0.6: 和D(6)=别 在有限变T:0下.电子藏发到更高能 不是每个电子获能
3 13 有限的温度 由于热能增加使电子动能增加 导致占据较高的能级 在T,能量为 ε的电子态被占据的几率是多少? 玻尔兹曼因子 exp(- ε/kBT) ? 对于声子 (玻色子) 电子是费米子 : 量子效应如 泡利不相容原理 属于统计力学的问题 (参考 appendix D) 费米-狄拉克 分布 exp[ ] ( ) ε µ /k T 1 1 f( ε ) − B + = 这里 µ 是对于电子数守衡的化学势 z 当 T=0 µ= εF, 当 ε= µ= εF, f(ε) 不连续地变化. z 在有限的 T, 当 ε =µ, f(ε)=1/2 z 当 (ε-µ) >> kBT, f(ε) 玻尔兹曼 分布 14 (1)0 ≤ f(ε,T) ≤ 1 0 2 4 6 8 10 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 f(ε) ε(A.U.) εF T=0.01TF T=0.02TF T=0.05TF T=0.5TF T=1.0TF (2) 当 T1/2 当 ε> µ, f(ε,T) = 0.6εF 在有限温度 (T≠0)下, 电子激发到更高能 态 和 U(T) 增加. εF εF D(ε)f(ε,T) ε 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 ε f(ε,T) T=0 T=0 T≠0 T≠0
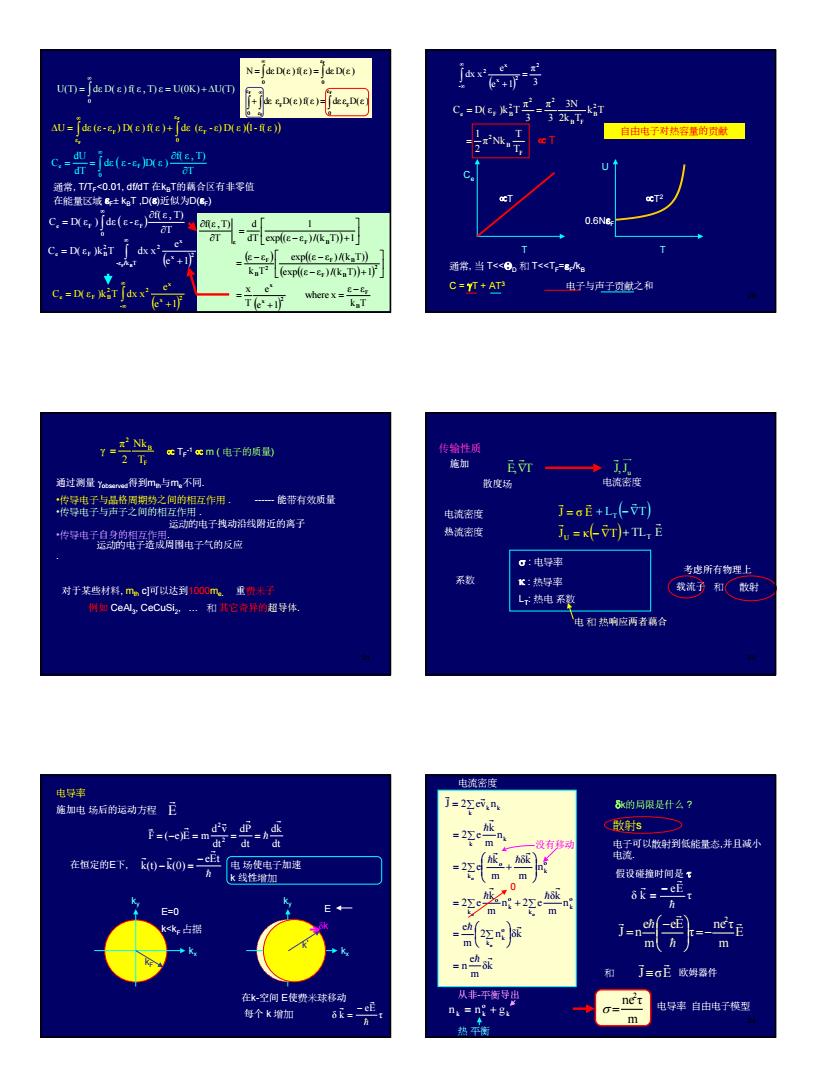
Neej在e U()=()RE.DE=UOK)+AU 白由电子对热务集的方献一 C.=-jse(e-c e)c.T C.-De )de(c e-{e- =2 常当TK<和TK<Tgk C-YT+AT —电子与声子之和 ?出m(电于的 传给性函 通过瑞量es得到m与m不洞. 散度场 互用 一能带有效 电流密身 j-0E+L(VT) 传好电于碧器隔电子的反应 热流密西 。:电导率 些所有物理上 载流和 干热电 电和热响应两者概合 nagE j-2K6i. 的局限是什么? 散一 没有男 出以版到低能量态,并且减小 w 假设碳时是 8= E=0 E 和了三G正欧姆器件 si- C图 热平
4 19 U(T) dε D( ε ) f( ε , T) ε U(0K) U(T) 0 = = + ∆ ∫ ∞ U dε (ε - ε ) D( ε ) f( ε ) dε (ε - ε) D( ε )( ) 1-f( ε ) F F ε 0 F ε ∫ F ∫ ∆ = + ∞ ∫ ∫ ∫ ∫ ∫ + = = = ∞ ∞ F F F F ε 0 F ε 0 F ε ε 0 0 dε ε D(ε )f(ε ) dε ε D(ε ) N dε D(ε )f(ε ) dε D(ε ) ( ) ∫ ∞ ∂ ∂ = = 0 e F T f( ε , T) dε ε - ε D( ε ) dT dU C 通常, T/TF<0.01, df/dT 在kBT的藕合区有非零值 在能量区域 εF± kBT ,D(ε)近似为D(εF) ( ) ∫ ∞ ∂ ∂ = 0 e F F T f( ε , T) C D( ε ) dε ε - ε ( ) ( ) ( ) ( ) ( ) ( ) k T ε ε where x e 1 e T x exp (ε ε )/(k T) 1 exp (ε ε )/(k T) k T ε ε exp (ε ε )/(k T) 1 1 dT d T f(ε ,T) B F 2 x x 2 F B F B 2 B F ε F B − = + = − + − − = − + = ∂ ∂ ( ) ∫ ∞ + = -ε /k T 2 x x 2 2 e F B F B e 1 e C D( ε )k T dx x ( ) ∫ ∞ ∞ + = - 2 x x 2 2 e F B e 1 e C D( ε )k T dx x 20 ( ) 3 π e 1 e dx x 2 - 2 x x 2 = + ∫ ∞ ∞ F B 2 2 B B F 2 2 2 e F B T T π Nk 2 1 k T 2k T 3N 3 π 3 π C D( ε )k T = = = ∝ T 自由电子对热容量的贡献 Ce T ∝T T U ∝T2 0.6NεF 通常, 当 T<<ΘD 和 T<<TF=εF/kB C = γT + AT3 电子与声子贡献之和 21 F B 2 T Nk 2 π γ = ∝ TF -1 ∝ m ( 电子的质量) 通过测量 γobserved得到mth与me不同. •传导电子与晶格周期势之间的相互作用 . - 能带有效质量 •传导电子与声子之间的相互作用 . 运动的电子拽动沿线附近的离子 •传导电子自身的相互作用. 运动的电子造成周围电子气的反应 . 对于某些材料, mth c]可以达到1000me. 重费米子 例如 CeAl3, CeCuSi2, . 和 其它奇异的超导体. 22 传输性质 施加 u E, T J,J r r r ∇ 散度场 电流密度 电流密度 热流密度 J κ( ) T J σ E U = −∇ = r r r r 系数 σ : 电导率 κ : 热导率 LT: 热电 系数 考虑所有物理上 载流子 和 散射 电 和 热响应两者藕合 L ( T) + T −∇ r TLT E r + 23 电导率 施加电 场后的运动方程 E r dt dk dt dP dt d v F ( e)E m 2 2 r h r r v r = − = = = 在恒定的E下, 电 场使电子加速 k 线性增加 kx ky E=0 k<kF 占据 kF E k kx ky k’ δk 在k-空间 E使费米球移动 每个 k 增加 τ eE δ k h r r − = h r r r eEt k(t) k(0) − − = 24 电流密度 δk m e n 2 n δk m e n m δk n 2 e m k 2 e n m δk m k 2 e n m k 2 e J 2 ev n o o o o k o k o k k o k o k o k o k k k k k k r h r h r h r h r h r h r h r r = = ∑ = ∑ + ∑ = ∑ + = ∑ = ∑ 0 没有移动 δk的局限是什么 ? 散射s 电子可以散射到低能量态,并且减小 电流. 假设碰撞时间是 τ τ eE δ k h r r − = E m ne τ τ eE m e J n 2 r h r r h =− − = J σE r r 和 ≡ 欧姆器件 m ne τ 2 σ = 电导率 自由电子模型 k o k k n = n + g 热 平衡 从非-平衡导出

⑧电真只是由部分以,速度运新的电子载流 调近“稳定”值 非平 新的老字态献相同电 time 一空穴 ©在经典留象里,所有的载流子,电子以定速度v迁移 J-neva =ne eEt=ne'tE=cE R=ptA mm ©只有费米面附近的电子对电流有 j-∑ei8 9.1x10-kg t45x0mr6xi017x0*m =nev,-ne(-v,) =25.104se 参与态的比例 所的 =(nr+nekevr ==4x108m=40nm .25k2y4=10 For E=1 voll/cm-va-0.43 m/sec 电子散射过程 区城1大角度非弹性数射(在高T下,电子声子) 时津声于数(T) 因此 ■这里怎略mp过程,该过程给不胸零指宽 ·在中等温区umklapp起支配作用。 区 区城Ⅱ小角度非弹性批射(在低T下,电子声子) ee散s pT)cT 区N 数连e声他 杂质敢5pD匹P一A q xx下可能的5
5 25 E E m ne τ m eEτ J nev ne 2 = d = = ≡ σ 逼近 “稳定态” 值 非平衡 δk time τ ∆k 0 @ 在经典图象里,所有的载流子,电子以恒定速度vd迁移. @ 只有费米面附近的电子对电流有贡献. δk<<kF kF kx ky 新的占据 态 nf 新的空态 ne ( ) ( ) f e F f F e F k k k n n ev n ev n e v J ev g = + = − − = ∑ r r 参与态 全部为vF 26 8.45 10 m ( ) 1.6 10 coul. 1.7 10 m 9.1 10 kg ne mσ τ m ne τ σ -8 2 28 3 19 31 2 2 × × × Ω × = = = − − − @ 电流只是由部分以vF速度巡游的电子载流. 新的满态 和空态贡献相同电流. nf 电子 ne 空穴 铜 V 横截面 A=wt 长 l R=ρl/A ρ(300K)= 1.7µΩcm n=8.45×1028 1/m3 vF= 1.57×106 m/sec = 2.5×10-14 sec l = vFτ = 4×10-8 m= 40 nm For E = 1 volt/cm vd ~0.43 m/sec 参与态的比例 6 F d F 10 v 2v ~ k 2δ k n δn − ≈ = I V 27 电子散射过程 m ne τ 2 σ = 导率 σ 受到散射s (τ, l)的限制 对于理想, 没有散射 σ→∞ 散射机制 ρ(T) T 0 IV III II I ρo 区域 I 大的 e-ph 散射s ρ(T) ∝ T 区域 II 小的 e-ph 散射s ρ(T) ∝ T5 区域 III e-e 散射s ρ(T) ∝ T2 区域 IV 杂质 散射s ρ(T) ∝ T0 自由电子模型 ~ ρo 28 区域 I 大角度非弹性散射 ( 在高T下,电子-声子 ) 散射率 ∝ # 声子数 ( ∝ T ) k r q r τ ∝ T-1 因此, σ ∝ T-1 ρ ∝ T 这里忽略umklapp 过程 ,该过程给出不同的结果. (在绝缘体中, 象k指数) 在中等温区 umklapp 起支配作用. 区域 II 小角度非弹性散射 (在低T下,电子-声子 ) Ek Ek ωq k k q h r r r = ± ′ = ± ′ 散射率 τ-1 ∝ # 声子数 ( ∝ T 3) 德拜 q << kF k' r k' r k r q r 有效碰撞因子 声子∝ T 2 29 区域 IV 弹性 散射 (杂质, 晶界, 缺陷,.) 杂质浓度等 . 决定 τ, l k r ' k r 能量守衡 Ek=Ek ’ τ = 常数 l =vFτ = 常数 , 不依赖 T 因此, σ(T) = σo , ρ(T) = ρo 恒定 区域 III 电子-电子 散射 k1 r 2 k r ' 2 k r ' 1 k r ' 2 ' 1 2 1 ' 2 ' 1 2 1 E E E E k k k k + = + + = + r r r r τ-1 ∝ T2 可能的态 σ(T) ∝ T-2 , ρ(T) ∝ T2 30 两个附加规则 : (1) 多散射机制 ρ ρ ρ ρ . . σ 1 σ 1 σ 1 σ 1 . τ 1 τ 1 τ 1 τ 1 e ph e e e impurity e e e impurity e ph e e e impurity e ph = + + + = + + + = + + + − − − − − − − − − Matthiessen规则 不精确但相当好 (2) 剩余电阻率 o ρ ρ(300K) R(0K) R(300K) RRR≡ = 声子支配 杂质支配 RRR → ∞, 理想晶体 通常, RRR ~ 102 to 104 (纯金属)

Matthiesen规则的实验现象 磁场中的运动 电场 =t=hg 改变船度 磁场 兽线 B=B 、罗仑兹力1运动方向 , 解 k(t)=A cos(t) 屋个不有的件品,具有不同的黄称器 =0 0 k,(t)=C owtes if利 McDonald Mendelssohn (1950) 。背 J.Linde,Ann.Phys.5.15(1932 Hal效型 B=B2 自由电于模型下,实空间和k空间都作园周运动 J==nev 肉xe=相定 在,的电子沿米面的球轨道运动。 自由电学米面还总 通常 白通语数 Hal效应计算密度和我流子符号 i=f+g×B=e正,B- p5=兰×停度) E-JBy=jBRn 热导率 太流来自声子一前章 — ot-0哈 热修的通量 亚单位时间流过单位面积的能量 用到自由电子 K:热导率系数 了=。正+LL 热电流密度 ● “m时 提释装翠 步的影明面少 热流密度 Ju=TLIE+K-VT) 而且声子前献可以与电子贡献相比拟 在开路的热测量牛 j=0→E-时 热导率与电导率的比率 事实上,对于大多辈 -n(信可 Lorentz数 侣产 iedemann-Franz定律 =2.45x10Wa-0/K2 实验值在表5
6 31 Matthiesen规则的实验现象 三个不同的样品,具有不同的缺陷浓 度. McDonald 和 Mendelssohn (1950). J. Linde, Ann. Phys. 5, 15 (1932). 32 磁 场中的运动 电 场 改变幅度 磁 场 改变方向 dt dk k B q F qv B dt dk F qE B E r h r h r r r r r h r r = × = × = = = m k r 罗仑兹力⊥运动方向 例如 : B=Bzˆ r 0 dt dk k m qB dt dk k m qB dt dk z x y y x = = − = 0 dt dk k m qB dt d k k m qB dt d k z y 2 2 y 2 x 2 2 x 2 = = − = − k (t) C k (t) A sin(ω t) k (t) A cos(ω t) z y c x c = = = 回旋圆周运动 ⊥ B 解 ωc=qB/m “回旋频率” 33 自由电子模型 下,实空间和 k- 空间都作园周运动 k ∝ε r = 恒定 ky kz kx B 在εF的电子沿费米面的球轨道运动. 对整个费米面都正确, 而不仅是对 自由电子. 对于输运性质,重要的因子是 ωcτ , 对两次连续散射事件里电子相位 的改变. 34 - ++++++ E FB e- , vd FE Hall 效应 磁场 电流 密度 x y J jxˆ nev xˆ z B Bzˆ = = d = r r e- x , vd y z B FB yˆ jBR yˆ ne jB E ( yˆ) n jB F qE qv B eE = ≡ H = + × = + − r r r v r r 横向 通常, ne 1 j B E R x y H ≡ = − Hall 系数 Hall 效应计算密度 和 载流子符号. = = ×( ) 厚度 I V j E ρ y x y H Hall 电阻率 [ Ωm ] 35 热导率 TH TL ∇T j U dx dT 热能的通量 jU = −κ 单位时间流过单位 面积的能量 κ : 热导率系数 E 0 U T j κ = ∇ ≡ − r 电流密度 热流密度 ( ) J TL E κ( ) T J σ E L T U T T = + − ∇ = + − ∇ r r r r r r 热电流密度 在开路的热测量中, κ T TL T κ T L J TL T L J 0 E 2 T T u T T ∇ = − − ∇ = ∇ = → = ∇ r r r r r r σ σ σ σ 2 T J 0 * U TL κ T j κ = − ∇ ≡ − = r 事实上, 对于大多数 金属和半导体来说, 第二项, LT,是很小的 . 因此, κ* = κ 36 热流来自声子 – 前章 Cv τ 3 1 Cv 3 1 κ 2 = g = g l 应用到自由电子 2 F F F B B 2 e mv 2 1 ε ε k T π nk 2 1 C = = Tτ m nk π 3 1 κ 2 2 B e = 在纯金属中,电子的贡献在所有T里都起主导 作用.在有杂质的金属或无序材料中, τ受杂质 碰撞的影响而减少, 而且声子贡献可以与电子贡献相比拟. 热导率与电导率的比率 T LT e k 3 π ne τ/m κ π nk Tτ / 3m 2 B 2 2 2 B 2 e ≡ = = σ 2 B 2 e k 3 π L Lorentz 数 = Lth = 2.45 × 10-8 Watt-Ω/K2 实验值在表5 Wiedemann-Franz定律