
第十一章电磁场和电磁波 §11-1位移电流麦克斯韦方程组 *§11-2电磁波 *§11-3电磁场的能量与动量 首页上页下页退出
首 页 上 页 下 页 退 出 1 第十一章 电磁场和电磁波 §11-1 位移电流 麦克斯韦方程组 *§11-2 电磁波 *§11-3 电磁场的能量与动量

§11-1位移电流麦克斯韦方程组 麦克斯韦,J.C. 首页上页下页退出
首 页 上 页 下 页 退 出 2 §11-1 位移电流 麦克斯韦方程组

11.1.1位移电流 1、电磁场的基本规律 对于静电场,由库仑定律和场强叠加原理,可以导 出描述电场性质的高斯定理和静电场环流定理。 ∮DdS=∑9 (11.1) ∮Edi=0 11.2) 首页上页下页退出
首 页 上 页 下 页 退 出 3 11.1.1 位移电流 1、电磁场的基本规律 对于静电场,由库仑定律和场强叠加原理,可以导 出描述电场性质的高斯定理和静电场环流定理. 0 (11.1) s D dS q = 0 (11.2) l E dl =

对于稳恒磁场,由毕奥-萨伐尔定律和场强叠加原理, 可以导出描述稳恒磁场性质的“高斯定理”和安培 环路定理 ∮B.ds=0 (11.3) fii=∑1。 (11.4) 首页上页下页退出
首 页 上 页 下 页 退 出 4 对于稳恒磁场,由毕奥—萨伐尔定律和场强叠加原理, 可以导出描述稳恒磁场性质的“高斯定理”和安培 环路定理 0 (11.3) s B dS = 0 (11.4) l H dl I =

对于变化的磁场,麦克斯韦提出,感生电动势现象 预示着变化的磁场周围产生了涡旋电场.于是,法拉 第电磁感应定律就表明了,在普遍(非稳恒)情况下电 场的环流定理应是 红- L.ds (11.5) 注意:式(11.5)中的电场E包括静电场和非稳恒电场 的总和,而静电场的环流定理式(11.2)只是它的一个 特例. 首页上页下页退出
首 页 上 页 下 页 退 出 5 对于变化的磁场,麦克斯韦提出,感生电动势现象 预示着变化的磁场周围产生了涡旋电场.于是,法拉 第电磁感应定律就表明了,在普遍(非稳恒)情况下电 场的环流定理应是 (11.5) l S B E dl d S t = − 注意:式(11.5)中的电场E包括静电场和非稳恒电场 的总和,而静电场的环流定理式(11.2)只是它的一个 特例

2、位移电流 在稳恒条件下,无论载流回路周围是真空还是磁介 质,安培环路定理都可以写成 ④Hi=∑。-Ji。us (11.6) 其中∑。是穿过以闭合回路为边界的任意曲面S 的传导电流,等于传导电流密度j在S面上的通量。 首页上页下页退出
首 页 上 页 下 页 退 出 6 在稳恒条件下,无论载流回路周围是真空还是磁介 质,安培环路定理都可以写成 0 0 (11.6) l s H dl I j dS = = 2、位移电流 其中 是穿过以闭合回路l为边界的任意曲面S 的传导电流,等于传导电流密度j 0在S面上的通量. 0 I
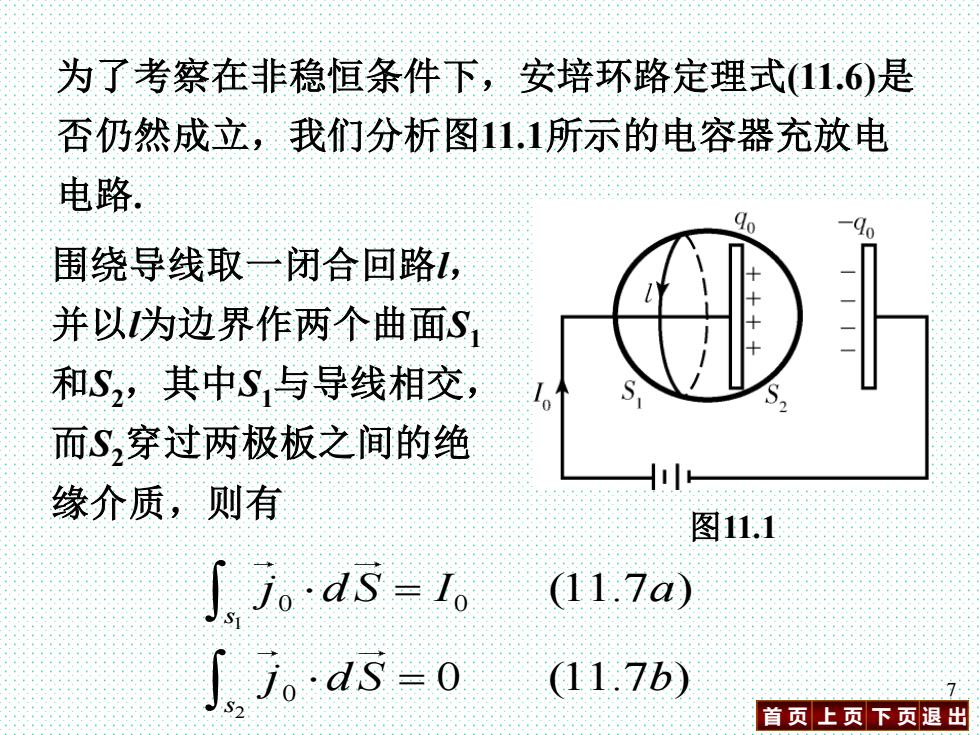
为了考察在非稳恒条件下,安培环路定理式(11.6)是 否仍然成立,我们分析图11.1所示的电容器充放电 电路 围绕导线取一闭合回路, 并以为边界作两个曲面S 和S,其中S与导线相交, 而S,穿过两极板之间的绝 缘介质,则有 图11.1 ∫j。ds=1。 (11.7a) ∫nj。·ds=0 (11.7b) 首页上页下页退出
首 页 上 页 下 页 退 出 7 为了考察在非稳恒条件下,安培环路定理式(11.6)是 否仍然成立,我们分析图11.1所示的电容器充放电 电路. 图11.1 围绕导线取一闭合回路l, 并以l为边界作两个曲面S1 和S2,其中S1与导线相交, 而S2穿过两极板之间的绝 缘介质,则有 1 2 0 0 0 (11.7 ) 0 (11.7 ) s s j d S I a j d S b = =

就是说,电容器的存在破坏了电路中传导电流的连 续性,使得以同一闭合回路所作的不同曲面S和S, 上穿过的电流不同,从而式(11.6)失去了意义. 因此,在非稳恒磁场的情况下安培环路定理式(11.6) 不再适用,必须以新的规律来代替它. 在图11.1的电容器充电过程中,传导电流在电容器 极板上终止的同时,将在极板表面引起自由电荷的 积累,即正极板十q增加、负极板一q增加.从而引 起两极板之间的电场随之变化。 首页上页下页退出
首 页 上 页 下 页 退 出 8 就是说,电容器的存在破坏了电路中传导电流的连 续性,使得以同一闭合回路l所作的不同曲面S1和S2 上穿过的电流不同,从而式(11.6)失去了意义. 因此,在非稳恒磁场的情况下安培环路定理式(11.6) 不再适用,必须以新的规律来代替它. 在图11.1的电容器充电过程中,传导电流在电容器 极板上终止的同时,将在极板表面引起自由电荷的 积累,即正极板+q0增加、负极板-q0增加.从而引 起两极板之间的电场随之变化

因为穿过任意闭合曲面S的传导电流密度的通量 ∮,j。·dS就是流出s面的电流,它应当等于S面内 部自由电荷在单位时间的减少率,即 ∮nj。·ds- (11.8) dt 其中S是由S,和S,构成的闭合曲面,q是积累在闭合 面S内的极板上的自由电荷,即图11.1所示的正极 板表面的自由电荷. 9 首页上页下页退出
首 页 上 页 下 页 退 出 9 其中S是由S1和S2构成的闭合曲面,q0是积累在闭合 面S内的极板上的自由电荷,即图11.1所示的正极 板表面的自由电荷. 因为穿过任意闭合曲面S的传导电流密度的通量 就是流出S面的电流,它应当等于S面内 部自由电荷在单位时间的减少率,即 0 S j dS 0 0 (11.8) S dq j d S dt = −

根据麦克斯韦的假设,对此非稳恒电场高斯定理仍 然成立,则有 ∮Dds=o 对此式两边求微商,得 只,Dd5手=% 把此式代入式(11.8),得 手,s手 .ds 10 首页上页下页退出
首 页 上 页 下 页 退 出 10 根据麦克斯韦的假设,对此非稳恒电场高斯定理仍 然成立,则有 对此式两边求微商,得 0 S D dS q = 0 S S d D dq D d S d S dt t dt = = 把此式代入式(11.8),得 0 S S D j d S d S t = −