
第二章 倒格子 我们如何确定晶体结构? (1)直接观察一直接地观察表面原子 体和表面 结构 STM 扫描隧道显微术 量子力学的隧穿 HREM 高分辨电子显微术 散射 电子波动光学 透护辉制 1
黄春晖 编制 1 第二章 倒格子 我们如何确定晶体结构? - 体和表面 结构 (1) 直接观察—直接地观察表面原子 STM 扫描隧道显微术 HREM 高分辨电子显微术 e- 散射 透射 电子波动光学 量子力学的隧穿 I V

(2)辐射波的衍射 -一传统方法 晶体 源 探测器 辐射 探测 1895 X-射线(光子) 强度vs.方向 1932 中子 强度vs.能量() 1897 电子 衍射区域:入~d 散射对干晶体结构很灵敏 黄者裤后刺 2
黄春晖 编制 2 (2) 辐射波的衍射 -传统方法 晶体 源 探测器 辐射 : X-射线 (光子) 中子 电子 探测 : 强度 vs. 方向 强度 vs. 能量 (λ) 1895 1932 1897 衍射区域 : λ ~ d 散射对于晶体结构很灵敏

光子 (电磁辐射) 1meV 1eV 1keV 1MeV E 1mm 1um 1nm 1pm + 入 红外区域(R) UV射线 X-射线 Gamma-射线 波粒二象性 ·用Maxwell方程描述电磁场以频率为v和波长为入的波形式传播 ·用量子论描述束缚能量E,(光子)的量子化, E-hv=hc/入 (A) 12.4 E(KeV) 能量10k©V的X-射线对应于1.24A的格子距离 黄春晖端制 3
黄春晖 编制 3 光子 (电磁辐射) 1meV 1eV 1keV 1MeV E 1mm 1µm 1nm 1pm λ 红外区域 (IR) UV 射线 X-射线 Gamma-射线 波粒二象性 • 用 Maxwell方程描述电磁场以频率为 ν和波长为 λ的波形式传播. • 用量子论描述束缚能量 E, (光子)的量子化. E=h ν =hc/λ E(KeV) 12.4 λ(A) = & 能量10keV的X-射线 对应于1.24Å的格子距离

粒子 波粒二象性 ·能量E=P22M(动量P) ·de Broglie波长入=h/P 中子 M=1.67x1027Kg 028 (A)= 当E=80meV时,入=1A √Eev 电子 m=0.91x10-30Kg 12 (A)= 当E=144eV时,=1A √Eev 黄毒牌编刺 4
黄春晖 编制 4 粒子 波粒二象性 • 能量 E = P2/2M (动量 P) • de Broglie 波长 λ=h/P 中子 M=1.67x10-27kg E(eV) 0.28 λ(A) = & 当 E=80meV时 , λ=1Å 电子 m=0.91x10-30Kg E(eV) 12 λ(A) = & 当 E=144eV时 , λ=1Å

10 X-ray Photon N eutron Electron 0.1 10 100 Energy Photon(KeV) Electron(100eV) Neutron(0.01eV) 黄碎端制 5
黄春晖 编制 5 1 1 0 1 0 0 0 . 1 1 1 0 X - r a y P hot o n N eut r o n E l e c t r o n wavelength (0.1nm ) E n e r g y : P h o t on( K e V ) E l e c t r on( 1 00eV ) N e u t r o n ( 0 . 01eV )

晶体的衍射波 Bragg定律:由晶体构成的干涉条件 2dsin0=nλ 入射射线 反射射线 Bragg反射只能出现在波长 d2d处 0 假设晶体是由原子面组成的,均 原子面 匀镜面产生反射 d sine -0=0 反射率~103~105 许多的样品面 黄毒牌编刺 6
黄春晖 编制 6 晶体的衍射波 Bragg 定律 :由晶体构成的干涉条件. 2d sinθ = nλ Bragg 反射只能出现在波长 λd2d处 d sinθ d θ 入射射线 反射射线 原子面 假设晶体是由原子面组成的,均 匀镜面产生反射. - θi=θr 反射率 ~ 10-3 ~ 10-5 许多的样品面

MgO FCC Angle (20) Bragg定律是被过分地简化.-忽略的功能 1.峰宽和强度的信息 2.来自不同原子的散射差别 3.原子周围的电荷分布 黄持碎端制 7
黄春晖 编制 7 MgO FCC Angle (2θ) Bragg 定律是被过分地简化. - 忽略的功能 1. 峰宽和强度的信息. 2. 来自不同原子的散射差别. 3. 原子周围的电荷分布

Laue定理:X-射线散射 考虑一般性的散射模型, 输入束 输出 样品n() 样品:电荷分布,n(0=电荷密度 入射束:面波 正=2江父=入射波矢 E=Ee-0) 0=2πf≡角频率 黄牌编场=k·T-t三波的相位 8
黄春晖 编制 8 Laue定理 : X-射线散射 考虑一般性的散射模型, dV O r r 样品 n(r) 输入束 k r k' r 输出束 样品 : 电荷分布, n(r)≡ 电荷密度 入射束 : 面 波 kˆ 入射波矢 2 k = ≡ r λπ (k r t) Ei Eo • −ω = r r i e 波的相位 角频率 k r ωt ω 2 f = • − ≡ = ≡ r r φ π
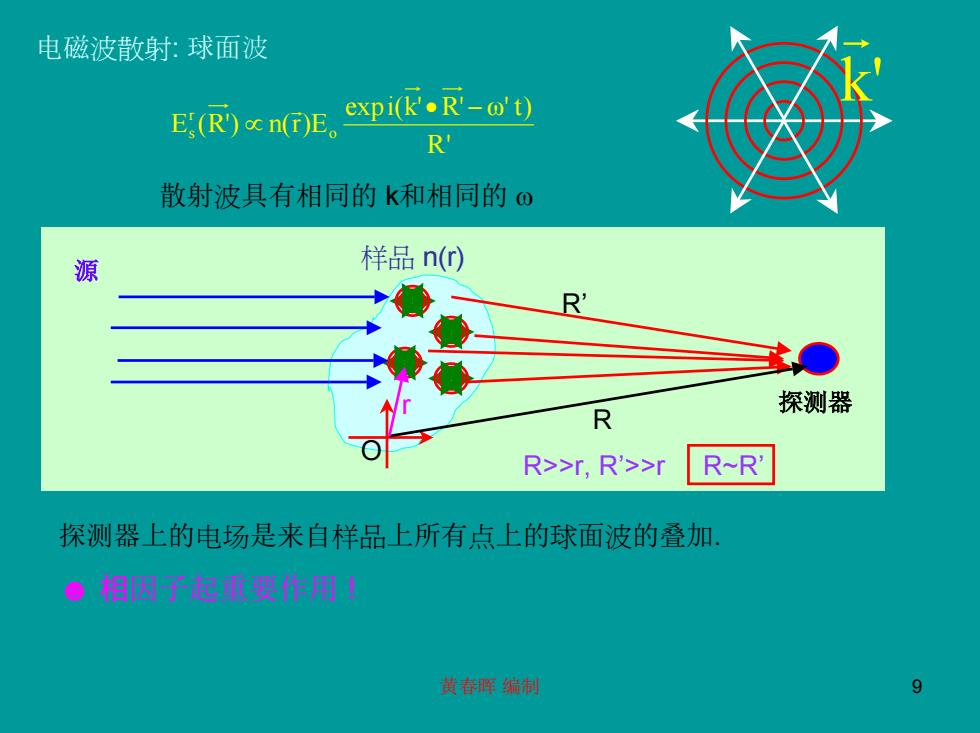
电磁波散射:球面波 E(R)cn(t)E。 expi(k'◆R'-o't) R 散射波具有相同的k和相同的。 源 样品n() R' 探测器 R R>>r,R'>> R~R' 探测器上的电场是来自样品上所有点上的球面波的叠加 色相西手超球婆在用! 黄春库编制 9
黄春晖 编制 9 k' r 电磁波散射: 球面波 R' expi(k' R' ω' t) E (R') n(r)Eo rs • − ∝ r 散射波具有相同的 k和相同的 ω 探测器 样品 n(r) r R R’ R>>r, R’>>r R~R’ 源 O 探测器上的电场是来自样品上所有点上的球面波的叠加. ☻ 相因子起重要作用 !
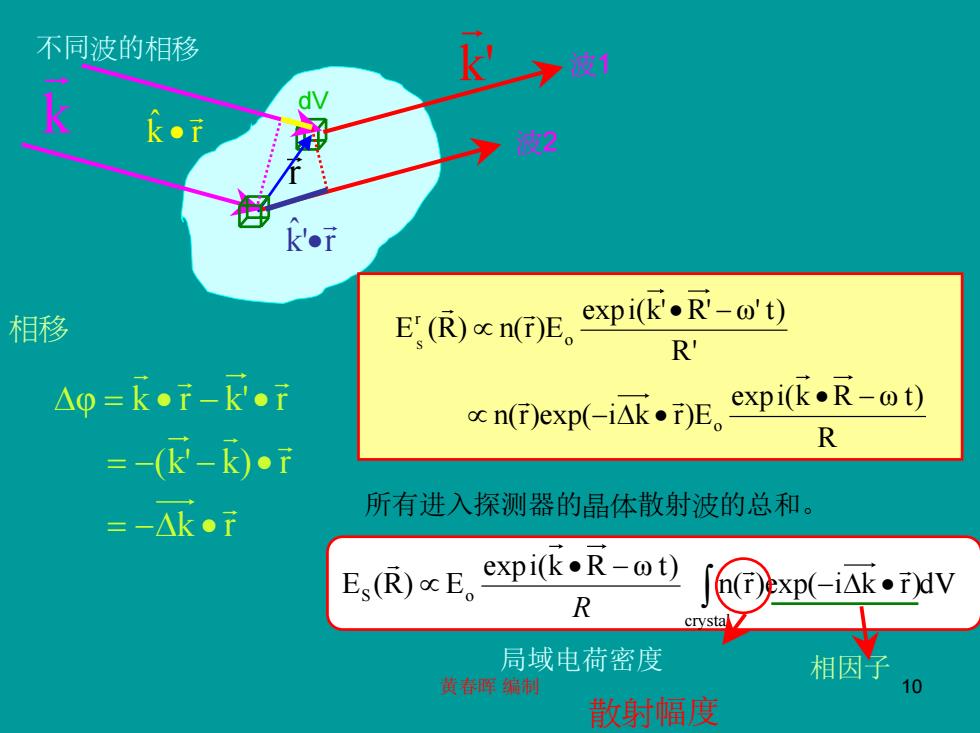
不同波的相移 k k●7 相移 E(R)n()Eexpi(KR-t) R' △p=k●f-k●T n(T)exp(ik)E expi(Rt) R =-(k-k)●T =-△k●7 所有进入探测器的晶体散射波的总和。 Es(R)cE expi(k●R-t) n(r) xp(-i△k●i)dV R crysta 局域电荷密度 相因子 黄参牌污村 10 散射幅度
黄春晖 编制 10 dV k r r r 不同波的相移 k r (k' k) r φ k r k' r r r r r r r = −∆ • = − − • ∆ = • − • 相移 R expi(k R ω t) n(r)exp( i k r)E R' expi(k' R' ω' t) E (R) n(r)E o o r S • − ∝ − ∆ • • − ∝ r r r r n(r)exp( i k r)dV expi(k R ω t) E (R) E crystal S o ∫ − ∆ • • − ∝ r r r R 局域电荷密度 相因子 波1 波2 k r ˆ r • k' r ˆ r • k' r 所有进入探测器的晶体散射波的总和。 散射幅度