第七章热力学基础 §7-1内能功和热量准静态过程 §7-2热力学第一定律 §7-3气体的摩尔热容量 §7-4绝热过程 §7-5循环过程卡诺循环 §7-6热力学第二定律 §7-7热力学第二定律的统计意义玻耳兹曼熵 §7-8卡诺定理 克劳修斯熵 首页上页下页退出
首 页 上 页 下 页 退 出 1 第七章热力学基础 §7-1 内能 功和热量 准静态过程 §7-2 热力学第一定律 §7-3 气体的摩尔热容量 §7-4 绝热过程 §7-5 循环过程 卡诺循环 §7-6 热力学第二定律 §7-7 热力学第二定律的统计意义 玻耳兹曼熵 §7-8 卡诺定理 克劳修斯熵

§7一1内能功和热量准静态过程 7.1.1内能功和热量 1、内能 理想气体内能 E= 理想气体内能的增量是温度的单值函数,只与始未状态 的温度有关,而与过程无关。 AE= M i RAT 实验表明:只要系统的始末状态相同,外界与系统交 换的能量是相同的,不论方式和具体过程如何。 首页上页下页退出
首 页 上 页 下 页 退 出 2 §7-1内能 功和热量 准静态过程 7.1.1 内能 功和热量 理想气体内能的增量是温度的单值函数,只与始末状态 的温度有关,而与过程无关。 R T i M M E mol = 2 实验表明:只要系统的始末状态相同,外界与系统交 换的能量是相同的,不论方式和具体过程如何。 RT i M M E mol 2 理想气体内能 = 1、内能

2、功 (1)在热力学中,功的定义与力学中一样,也是与物体的 宏观位移相联系。 dA-F dl (2)功使系统的机械运动状态变化,也能使系统的热力学状 态(内能)发生变化。 (3)功是系统与外界交换能量的一种方式,是系统与外界交 换的能量的量度,与变化过程紧密相关,故而功是过程量。 (4)在热学中,功是外界的有序运动能量与系统无序热运 动能量之间的转换。 首页上页下页退出
首 页 上 页 下 页 退 出 3 2、功 dA F dl = (1) 在热力学中,功的定义与力学中一样,也是与物体的 宏观位移相联系。 (2) 功使系统的机械运动状态变化,也能使系统的热力学状 态(内能)发生变化。 (3) 功是系统与外界交换能量的一种方式,是系统与外界交 换的能量的量度,与变化过程紧密相关,故而功是过程量。 (4) 在热学中,功是外界的有序运动能量与系统无序热运 动能量之间的转换

3、热量 (1)当系统与外界有温差时,系统与外界传递无序热运 动能量的方式叫做热传递。 (2)热传递也是使系统的热力学状态发生改变的方式。 (3)通过热传递方式交换的能量称热量。交换的热量与 过程密切相关,故热量也是过程量。 ※热力学系统与外界交换能量有两种方式 做功、热传递 功和热量都是能量变化的量度: 单位:焦耳J 热、功转换关系为1cal=4.18J 首页上页下页退出
首 页 上 页 下 页 退 出 4 3、热量 (1)当系统与外界有温差时,系统与外界传递无序热运 动能量的方式叫做热传递。 (2)热传递也是使系统的热力学状态发生改变的方式。 (3)通过热传递方式交换的能量称热量。交换的热量与 过程密切相关,故热量也是过程量。 ※热力学系统与外界交换能量有两种方式 做功、热传递 功和热量都是能量变化的量度: 单位:焦耳 J 热、功转换关系为 1cal=4.18J

71.2准静态过程 热力学系统在外界影响下发生的状态变化称为热力学过程 ,简称过程。 在过程进行中的任一时刻,系统都无限接近平衡态,这 样的过程称为准静态过程。 *准静态过程是理想化过程、无限具有相对意义, 系统从一个平衡态变到相邻平衡态所经过的时间叫系统的 弛豫时间。 首页上页下页退出
首 页 上 页 下 页 退 出 5 7.1.2 准静态过程 * 准静态过程是理想化过程、无限具有相对意义, 热力学系统在外界影响下发生的状态变化称为热力学过程 ,简称过程。 在过程进行中的任一时刻,系统都无限接近平衡态,这 样的过程称为准静态过程。 系统从一个平衡态变到相邻平衡态所经过的时间叫系统的 弛豫时间
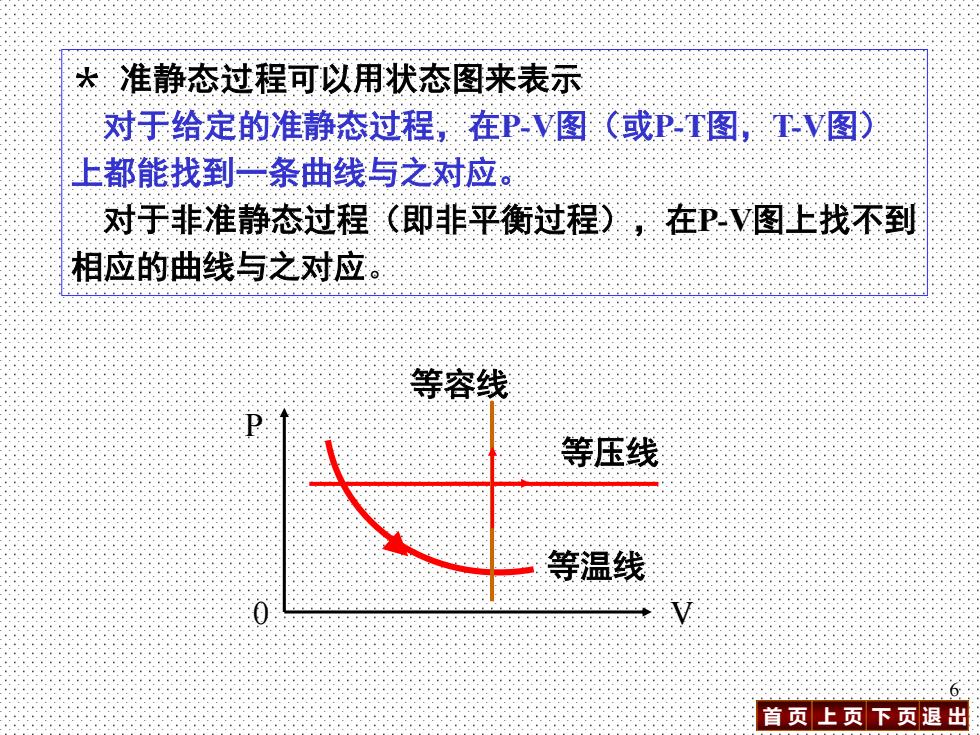
大准静态过程可以用状态图来表示 对于给定的准静态过程,在PV图(或P-T图,TV图) 上都能找到一条曲线与之对应。 对于非准静态过程(即非平衡过程),在PV图上找不到 相应的曲线与之对应。 等容线 等压线 等温线 首页上页下页退出
首 页 上 页 下 页 退 出 6 * 准静态过程可以用状态图来表示 对于给定的准静态过程,在P-V图(或P-T图,T-V图) 上都能找到一条曲线与之对应。 对于非准静态过程(即非平衡过程),在P-V图上找不到 相应的曲线与之对应。 P 0 V 等温线 等压线 等容线

7,1.3准静态过程的功与热量 1、准静态过程的功 (1)设有一密封气体,推动活塞从状态变化到状态川的 过程是准静态过程,设活塞在某一位置时,容器内气体压强 为P,活塞面积为$,在气体推动活塞移动d过程中,气体对 活塞做的元功为dA,则 dA=Fdl=pSdl=pd亚 d 若系统经过有限的准静态过程,其始末状态的体积为V和V2, 则总功为 A=pdr 首页上页下页退出
首 页 上 页 下 页 退 出 7 1、准静态过程的功 (1)设有一密封气体,推动活塞从状态I变化到状态II的 过程是准静态过程,设活塞在某一位置时,容器内气体压强 为P,活塞面积为S,在气体推动活塞移动d过程中,气体对 活塞做的元功为dA,则 dA = Fdl = pSdl = pdV 若系统经过有限的准静态过程,其始末状态的体积为V1和V2, 则总功为 2 1 V V A pdV = S P dl dA 7.1.3 准静态过程的功与热量
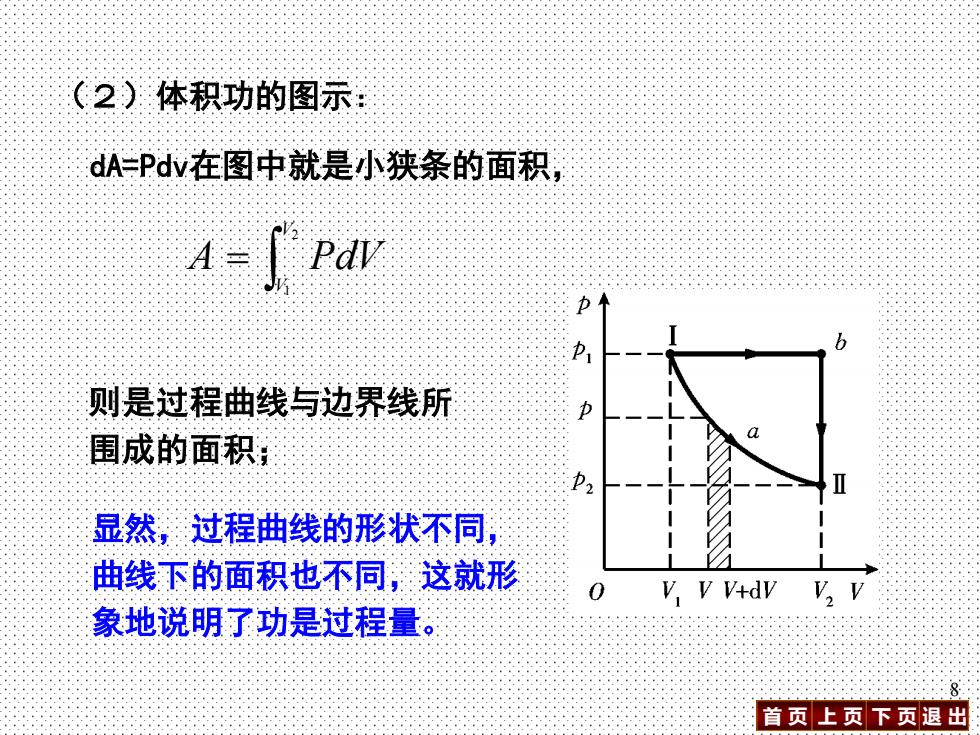
(2)体积功的图示: dA-Pdv在图中就是小狭条的面积, P 则是过程曲线与边界线所 围成的面积: 显然,过程曲线的形状不同, 曲线下的面积也不同,这就形 VVV+dv V,V 象地说明了功是过程量。 首页上页下页退出
首 页 上 页 下 页 退 出 8 (2)体积功的图示: 显然,过程曲线的形状不同, 曲线下的面积也不同,这就形 象地说明了功是过程量。 dA=Pdv在图中就是小狭条的面积, = 2 1 V V A PdV 则是过程曲线与边界线所 围成的面积;

2、准静态过程的热量 (1)比热 Q-MC (T2-T> do=MCdT C为比热,一般地,比热是温度的函数,但当温度变化不 大时,C可认为常数,即一般情况下 -MCdT (2)热容量 Q-MC 如果取M=1Mmo,则Q=MnC=Cm,Cm叫做摩尔热容量。 过程不同,气体摩尔热容量C值有较大差异。 首页上页下页退出
首 页 上 页 下 页 退 出 9 2、准静态过程的热量 (1)比热 dQ = MCdT C为比热,一般地,比热是温度的函数,但当温度变化不 大时,C可认为常数,即一般情况下 = 2 1 T T Q MCdT (2)热容量 Q=MC 过程不同,气体摩尔热容量 Cm值有较大差异。 Q=MC(T2 -T1) 如果取M=1Mmol,则 Q=MmolC=Cm ,Cm叫做摩尔热容量

定体过程 Q.M M C (-D C,二定体摩尔热容量 定压过程 0, Mc,U,-用 C。一定压摩尔热容量 10 首页上页下页退出
首 页 上 页 下 页 退 出 10 定体过程 ( ) C T2 T1 M M Q v mol v = − Cv─定体摩尔热容量 定压过程 ( ) C T2 T1 M M Q p mol p = − Cp─定压摩尔热容量