
第五章机械波 在研究了机械振动的基本内容以后,从本节开始讨论机械振动的传播,即机械波。这耳 涉及关于机械波的形成、传播等内容。除了这部分内容本身属于基础知识外,它也为研究其 他领域的波动问题提供了必不可少的知识准备。 5.1机械波的产生和传播 5.11机械波产生条件 机械振动在弹性介质(固体、液体、气体)内传播就形成了机械波,机械波从振动方向 与传播方向之间的差别可区分横波和纵波。 固体弹性介质里横波的形戒 绳上的波其形成靠的是绳上各部分之间互相作用的张力,这种张力使得介质各部分有恢 复捧齐的趋势 如果是一块固体,可设想划分为许多竖直的薄层,如图15-3所示当在左侧面上施加 个向上的力了时,则左侧面便向上移动,各薄层也就跟随者依次向上移动,这种形变叫剪切 发生剪切的固体有恢复原状(即各层排齐)的趋势,这种性质叫做剪切弹性,剪切弹性具体 体现在相邻两薄层之间有切向的相互作用力,以图153(b)为例,右边的薄层对左边的海 层施加向下的作用力,而左边的薄层对右边的薄层施加向上的作用力,这种因发生剪切而出 现的切向恢复力叫剪切弹性力,它正是横波在固体介质中传播的内因在或依据。 a222 (c) d 图15-3(a) 图15-3(b) 图154固定弹性介质里的横波 试设想有一长条形固体介质由许多薄层紧挨排列而成,为分析方便起见,把它们编号为 0,1,23,.,当层0开始向横向振动时,它与层1便不再排齐,即发生了剪切,这时便产 生相应的剪切弹性力,层1对层0有向下的作用力,此为阻力,层0对层1有向上的拉力, 它促使层1跟随层0向上运动,但层1的步调落后于层0,同样层1又带动层2,层2带动 层3 一层带动一层,振动便传播出去,这跟绳上波的形成类似,于是固体介质中的 横被也就这样形成了
第五章 机械波 在研究了机械振动的基本内容以后,从本节开始讨论机械振动的传播,即机械波。这里 涉及关于机械波的形成、传播等内容。除了这部分内容本身属于基础知识外,它也为研究其 他领域的波动问题提供了必不可少的知识准备。 5.1 机械波的产生和传播 5.1.1 机械波产生条件 机械振动在弹性介质(固体、液体、气体)内传播就形成了机械波,机械波从振动方向 与传播方向之间的差别可区分横波和纵波。 固体弹性介质里横波的形成 绳上的波其形成靠的是绳上各部分之间互相作用的张力,这种张力使得介质各部分有恢 复排齐的趋势。 如果是一块固体,可设想划分为许多竖直的薄层,如图 15-3 所示当在左侧面上施加一 个向上的力 f 时,则左侧面便向上移动,各薄层也就跟随着依次向上移动,这种形变叫剪切。 发生剪切的固体有恢复原状(即各层排齐)的趋势,这种性质叫做剪切弹性,剪切弹性具体 体现在相邻两薄层之间有切向的相互作用力,以图 15-3(b)为例,右边的薄层对左边的薄 层施加向下的作用力,而左边的薄层对右边的薄层施加向上的作用力,这种因发生剪切而出 现的切向恢复力叫剪切弹性力,它正是横波在固体介质中传播的内因在或依据。 f s 0 1 2 3 4 5 6 7 8 x (a) (b) (c) (d) (e) (f) 图 15-3(a) 图 15-3(b) 图 15-4 固定弹性介质里的横波 试设想有一长条形固体介质由许多薄层紧挨排列而成,为分析方便起见,把它们编号为 0, 1, 2, 3, . . 当层 0 开始向横向振动时,它与层 1 便不再排齐,即发生了剪切,这时便产 生相应的剪切弹性力,层 1 对层 0 有向下的作用力,此为阻力,层 0 对层 1 有向上的拉力, 它促使层 1 跟随层 0 向上运动,但层 1 的步调落后于层 0,同样层 1 又带动层 2,层 2 带动 层 3,.,一层带动一层,振动便传播出去,这跟绳上波的形成类似,于是固体介质中的 横波也就这样形成了

发生张变的介质都有恢复原状的趋势,这种由张变出现的张变弹性力(拉力或推力) 将使得介质中某质点的振动由近及远的传播出去,因而在弹性介质(固体、液体或气体)中 形成纵波,传播纵波 所以机械波的产生条件为:机械振动和弹性介质。 5.1.2横波和纵波 1、取一根较长的柔软细绳,将它的一端固定,另 一端用手拿者,并轻轻拉直,然后用握绳的手上下抖动 一次,就会出现一个“峰”和一个“谷”沿绳向固定端 移动,如图151所示。如果手上下连续地抖动,就会 有连续的“峰”和“谷”沿绳移动。这种振动的传播现 象就叫做波,因为是用手握住绳的一端上下抖动,即振 动,此振动沿绳传播,这便是绳上的波。用手握住的绳 图11-1绳上波 端便为波源,绳是传播绳上波的介质(或叫媒质) 下面具体说明振动是怎样在绳上传播的,即绳上的波是怎样形成的。 可以把绳子看作由一连串相互联系着的质点组成,给这些质点编上号,从手持端开始 依次为0,1,2,3,当绳子被轻轻拉直时,这些质点也就互相拉紧,这互相拉紧的力便是 绳中的张力,依靠彼此间相互作用若的张力,形成一条直线,这就是绳子处于平衡时的位形 (或叫形相). 当手握住绳头抖动时,首先是质点0跟随着向正向一侧移动,于是质点0与1不再排齐 这时它们之间的张力便有驱使它们恢复排齐的趋势。于是质点0从前面拉质点1,带动者质 点1向正向移动时,质点1同时又从后面拉质点0,这就是抖动绳头时手上所感到的阻力, 但毕竟不能阻止质点0继续向正向移动,因而质点1的步调也总是稍稍滞后于质点0,同样 质点1又带动者质点2,质点2又稍稍滞后于质点1,质点2又带动质点3,.,照此下 一个个质点依次带动自己邻近的另一个质点相维的离开各自的平衡位置 经过14周期,质点0正好到达正向的最大偏离位置,质点1落后一些,质点2又落后 质点1一些,而质点3刚要离开自己的平衡位置向正向移动,如图302(b)所示情形。 质点0达到正向最大偏离位置后随之回头向自己的平衡位置移动,又经过14周期,即 到12周期时,质点0达到自己的平衡位置,正朝负方向移动,此时质点1被质点0带动者 在达到正向最大偏离位置后也回头向它自己的平衡位置移动,但还未到达平衡位置,质点2 被质点1带动经过自己的正向最大偏离位置回头向平衡位置移动,但落在质点1后面一些, 质点3被质点2带动正好到达正向最大偏离位置刚要回头,而质点4落后于质点3,质点5 落后于质点4,质点6刚要离开平衡位置向正向移动。其余质点均未开始运动,见图15-2 (c)所示
2 发生张变的介质都有恢复原状的趋势,这种由张变出现的张变弹性力(拉力 或推力) 将使得介质中某质点的振动由近及远的传播出去,因而在弹性介质(固体、液体或气体)中 形成纵波,传播纵波。 所以机械波的产生条件为:机械振动和弹性介质。 5.1.2 横波和纵波 1、取一根较长的柔软细绳,将它的一端固定,另 一端用手拿着,并轻轻拉直,然后用握绳 的手上下抖动 一次,就会出现一个“峰”和一个“谷”沿绳向固定端 移动,如图 15-1 所示。 如果手上下连续地抖动,就会 有连续的“峰”和“谷”沿绳移动。这种振动的传播现 象就叫做波,因为是用手握住绳的一端上下抖动,即振 动,此振动沿绳传播,这便是绳上的波。用手握住的绳 端便为波源,绳是传播绳上波的介质(或叫媒质). 下面具体说明振动是怎样在绳上传播的,即绳上的波是怎样形成的。 可以把绳子看作由一连串相互联系着的质点组成,给这些质点编上号,从手持端开始, 依次为 0, 1, 2, 3, .,当绳子被轻轻拉直时,这些质点也就互相拉紧,这互相拉紧的力便是 绳中的张力,依靠彼此间相互作用着的张力,形成一条直线,这就是绳子处于平衡时的位形 (或叫形相). 当手握住绳头抖动时,首先是质点 0 跟随着向正向一侧移动,于是质点 0 与 1 不再排齐, 这时它们之间的张力便有驱使它们恢复排齐的趋势。于是质点 0 从前面拉质点 1,带动着质 点 1 向正向移动时,质点 1 同时又从后面拉质点 0,这就是抖动绳头时手上所感到的阻力, 但毕竟不能阻止质点 0 继续向正向移动,因而质点 1 的步调也总是稍稍滞后于质点 0 . 同样, 质点 1 又带动着质点 2,质点 2 又稍稍滞后于质点 1,质点 2 又带动质点 3,.,照此下 去,一个个质点依次带动自己邻近的另一个质点相继的离开各自的平衡位置。 经过 1/4 周期,质点 0 正好到达正向的最大偏离位置,质点 1 落后一些,质点 2 又落后 质点 1 一些,而质点 3 刚要离开自己的平衡位置向正向移动,如图 30-2(b)所示情形。 质点 0 达到正向最大偏离位置后随之回头向自己的平衡位置移动,又经过 1/4 周期,即 到 1/2 周期时,质点 0 达到自己的平衡位置,正朝负方向移动,此时质点 1 被质点 0 带动着 在达到正向最大偏离位置后也回头向它自己的平衡位置移动,但还未到达平衡位置,质点 2 被质点 1 带动经过自己的正向最大偏离位置回头向平衡位置移动,但落在质点 1 后面一些, 质点 3 被质点 2 带动正好到达正向最大偏离位置刚要回头,而质点 4 落后于质点 3,质点 5 落后于质点 4,质点 6 刚要离开平衡位置向正向移动。其余质点均未开始运动,见图 15-2 (c)所示。 手持端 图 11-1 绳上波
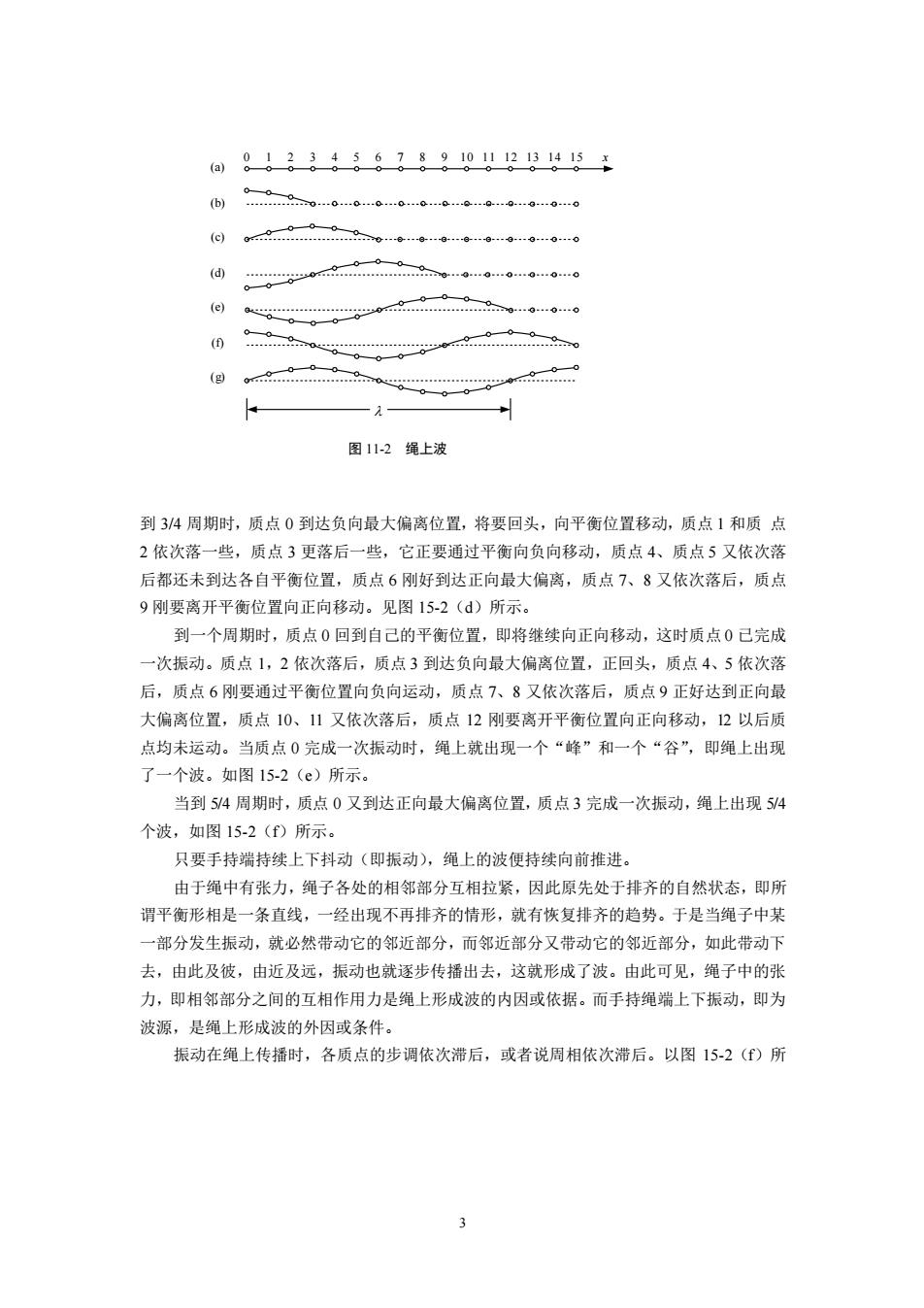
00↓3g4;6?;g002B1415 g 0000 90.0.0 0 图112绳上波 到34周期时,质点0到达负向最大偏离位置,将要回头,向平衡位置移动,质点1和质点 2依次落一些,质点3更落后一些,它正要通过平衡向负向移动,质点4、质点5又依次落 后都还未到达各自平衡位置,质点6刚好到达正向最大偏离,质点7、8又依次落后,质点 9刚要离开平衡位置向正向移动。见图15-2()所示。 到一个周期时,质点0回到自己的平衡位置,即将继续向正向移动,这时质点0已完成 一次振动。质点1,2依次落后,质点3到达负向最大偏离位置,正回头,质点4、5依次落 后,质点6刚要通过平衡位置向负向运动,质点7、8又依次落后,质点9正好达到正向最 大偏离位置,质点10、11又依次落后,质点12刚要离开平衡位置向正向移动,2以后质 点均未运动。当质点0完成一次振动时,绳上就出现一个“峰”和一个“谷”,即绳上出现 了一个波。如图15-2()所示。 当到54周期时,质点0又到达正向最大偏离置,质点3完成一次振动,绳上出现5/4 个波,如图15-2()所示。 只要手持端持续上下抖动(即振动),绳上的波便持续向前推进 由于绳中有张力,绳子各处的相邻部分互相拉紧,因此原先处于排齐的自然状态,即所 谓平衡形相是一条直线,一经出现不再排齐的情形,就有恢复排齐的趋势。于是当绳子中某 一部分发生振动,就必然带动它的邻近部分,而邻近部分又带动它的邻近部分,如此带动下 去,由此及彼,由近及远,振动也就逐步传播出去,这就形成了波。由此可见,绳子中的张 力,即相邻部分之间的互相作用力是绳上形成波的内因或依据。而手持绳端上下振动,即为 波源,是绳上形成波的外因或条件。 振动在绳上传播时,各质点的步调依次滞后,或者说周相依次滞后。以图15-2()所
3 到 3/4 周期时,质点 0 到达负向最大偏离位置,将要回头,向平衡位置移动,质点 1 和质 点 2 依次落一些,质点 3 更落后一些,它正要通过平衡向负向移动,质点 4、质点 5 又依次落 后都还未到达各自平衡位置,质点 6 刚好到达正向最大偏离,质点 7、8 又依次落后,质点 9 刚要离开平衡位置向正向移动。见图 15-2(d)所示。 到一个周期时,质点 0 回到自己的平衡位置,即将继续向正向移动,这时质点 0 已完成 一次振动。质点 1,2 依次落后,质点 3 到达负向最大偏离位置,正回头,质点 4、5 依次落 后,质点 6 刚要通过平衡位置向负向运动,质点 7、8 又依次落后,质点 9 正好达到正向最 大偏离位置,质点 10、11 又依次落后,质点 12 刚要离开平衡位置向正向移动,12 以后质 点均未运动。当质点 0 完成一次振动时,绳上就出现一个“峰”和一个“谷”,即绳上出现 了一个波。如图 15-2(e)所示。 当到 5/4 周期时,质点 0 又到达正向最大偏离位置,质点 3 完成一次振动,绳上出现 5/4 个波,如图 15-2(f)所示。 只要手持端持续上下抖动(即振动),绳上的波便持续向前推进。 由于绳中有张力,绳子各处的相邻部分互相拉紧,因此原先处于排齐的自然状态,即所 谓平衡形相是一条直线,一经出现不再排齐的情形,就有恢复排齐的趋势。于是当绳子中某 一部分发生振动,就必然带动它的邻近部分,而邻近部分又带动它的邻近部分,如此带动下 去,由此及彼,由近及远,振动也就逐步传播出去,这就形成了波。由此可见,绳子中的张 力,即相邻部分之间的互相作用力是绳上形成波的内因或依据。而手持绳端上下振动,即为 波源,是绳上形成波的外因或条件。 振动在绳上传播时,各质点的步调依次滞后,或者说周相依次滞后。以图 15-2(f)所 0 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 x (a) (b) (c) (d) (e) (f) ( g) 图 11-2 绳上波

示时刻为例,质点0达到正向最大偏离位置,其周相是0或2π,质点1的周相滞后6,其 周相为,质点2的周相又滞后工,其周相为”,质点3处于平衡位置,其周相是” 质点6的周相是π,质点9的周相是?,质点2的周相是0或2m(同正向最大偏离位置), 周相依次滞后,这说明振动的传播需要时间,振动传播的速度叫做波速。绳上波的波速 经理论研究由下式给出数=,式中T是绳中张力,P是绳子的线密度,即单位长的质 量。由此可见,张力T越大,波速越大,线密度越小,波速就越大。这是容易理解的,张力 越大,对邻近质点的带动力越大,所以振动传播得快,绳子越轻,各个质点的惯性就越小, 也就容易被带动,因此振动传播也就越快。这一想法就反映在理论研究的结果中。 在图152中可以看到,质点0开始振动时即由平衡位置朝正向运动时的周相设为” 则经14周期,振动传到质点3,其周相也是”,又经14周期,振动传到质点6,其周相也 是,再经14周期,振动传到质点9,其周期也是,.,如此传播下去。 2、纵波 前面介绍了绳上 02g49678g02g4560 波,固体弹性介质里 0 的波,这都是横波, T-4 横波的特点是其振动 方向与波的传播方向 垂直。这里介绍另 T 种波,这种波振动方 向与传播方向平行。 这叫做纵波,例如声 (g) 波就是典型的横波 这种波的形成与介质 图115弹性介质里的纵波 中另一种弹性形变一 一张变有关。介质发生伸长与缩短的形变叫张(长)变,发生张变的介质(固体、流体和气 体)都有恢复原状的趋势,这种性质叫张变弹性,它是纵波在介质里传播的内因或依据。 弹性介质中的纵波是如何形成的呢? 把弹性介质设想为由一连串联系若的质点组成,为分析方便起见也把它们编号为0,1, 2,当质点0开始作纵向振动时,例如先朝质点1移动时(以下称该方向为正方向),于
4 示时刻为例,质点 0 达到正向最大偏离位置,其周相是 0 或 2 ,质点 1 的周相滞后 6 ,其 周相为 6 11 ,质点 2 的周相又滞后 6 ,其周相为 3 5 ,质点 3 处于平衡位置,其周相是 2 3 , 质点 6 的周相是 ,质点 9 的周相是 2 ,质点 12 的周相是 0 或 2 (同正向最大偏离位置). 周相依次滞后,这说明振动的传播需要时间,振动传播的速度叫做波速。绳上波的波速 经理论研究由下式给出 线 波 T v = ,式中 T 是绳中张力, 线 是绳子的线密度,即单位长的质 量。由此可见,张力 T 越大,波速越大,线密度越小,波速就越大。这是容易理解的,张力 越大,对邻近质点的带动力越大,所以振动传播得快,绳子越轻,各个质点的惯性就越小, 也就容易被带动,因此振动传播也就越快。这一想法就反映在理论研究的结果中。 在图 15-2 中可以看到,质点 0 开始振动时即由平衡位置朝正向运动时的周相设为 2 3 , 则经 1/4 周期,振动传到质点 3,其周相也是 2 3 ,又经 1/4/周期,振动传到质点 6,其周相 也 是 2 3 ,再经 1/4 周期,振动传到质点 9,其周期也是 2 3 ,.,如此传播下去。 2、纵波 前面介绍了绳上 波,固体弹性介质里 的波,这都是横波, 横波的特点是其振动 方向与波的传播方向 垂直。这里介绍另一 种波,这种波振动方 向与传播方向平行, 这叫做纵波,例如声 波就是典型的横波。 这种波的形成与介质 中另一种弹性形变— —张变有关。介质发生伸长与缩短的形变叫张(长)变,发生张变的介质(固体、流体和气 体)都有恢复原状的趋势,这种性质叫张变弹性,它是纵波在介质里传播的内因或依据。 弹性介质中的纵波是如何形成的呢? 把弹性介质设想为由一连串联系着的质点组成,为分析方便起见也把它们编号为 0, 1, 2, .,当质点 0 开始作纵向振动时,例如先朝质点 1 移动时(以下称该方向为正方向),于 x (a) (b) (c) (d) (e) (f) (g) 0 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 4 T 2 T 4 3T 4 5T 2 3T 0 T 图 11-5 弹性介质里的纵波

是质点0与1相互压紧,压紧时便有恢复原状的趋势,相互间便出现相互作用的推力,即质 点1对质点0施以推力,此即阻力,质点0推质点1,使质点1跟随质点0运动,但步调要 稍落后一些,同样质点1又推质点2,使质点2也跟随质点1运动,但步调又稍落后于质点 1,质点2又推质点3,.,经14周期,如图155(b)所示,质点0到达正向最大偏离 位置,质点1,2依次也向各自的正向运动,但依次滞后,质点3则要开始移动,质点3以 后的质点都没有动。 质点0到达正向最大偏离位置便回头向平衡位置移动,这时质点0和质点1之间因距离 拉开,而相互之间出现拉力,质点1拉质点0,是阻力,质点0拉质点1是促使质点1跟随 质点0向负方向移动,经过1/4周期,如图15-5(c)所示,质点0正好到达平衡位置,正 朝负方向移动,质点1也胡负方向移动,但还未到达平衡位置,仍偏在正的一边,质点2 又滞后一些,也偏在正的一边,质点3刚到达正向最大偏离位置,质点4,5也朝正向移动, 但依次滞后一些,质点6刚要开始向正向移动。又经过14周期,各质点的位置如图155 (d)所示。这时质点6到达正向最大偏离位置,质点9刚要开始向正向移动,再经1/4周 期,各质点位置如图155(©)所示,质点0回到平衡位置,质点3到负向最大偏离位置, 质点6到达平衡位置正要向负方向继续移动,质点9到达正向最大偏离位置,刚要回头,质 点12将要向正方向移动。到54周期时,如图15-5()所示。质点0又到达正向最大偏 离位置,质点3到达平衡位置,质点6到达负向最大偏离位置,质点9到达平衡位置,质 点12到达正向最大偏离位置,质点15将要向正向移动。 由于质点作纵向运动,介质中便出现疏部与密部,质点0完成一次振动,即从图155 (a)到(c),介质里出现一个疏部和一个密部,即出现一个波。质点0继续不断地振动, 介质里就出现一个接一个的传播着的疏部和密部,这就形成了介质中的纵波或者叫疏密波。 5.13、波阵面和波射线 一维波的描述相对地比较简单,但对于空间波的描述相对地说就比较复杂一些。因此有必 要采用变通的办法,即采用波面、波前和波射线这些概念,就会变得比较方便,而且图像也 比较清晰 波阵面振动周相相同的各点连成的曲面称为波阵面,又叫同相面或简称波面 波前最前面的(或者说领先的)波阵面称为波前。 波射线波的传播方向称为波射线或波线。在各向同性介质中,波线总是垂直于波面的。 依照波面的形状不同,来区别二种不同的空间波。它们都是最重要的而且具有代表性的 空间波。 球面波波面为球形的波,它是由点状波源在各向同性介质中发出的波
5 是质点 0 与 1 相互压紧,压紧时便有恢复原状的趋势,相互间便出现相互作用的推力,即质 点 1 对质点 0 施以推力,此即阻力,质点 0 推质点 1,使质点 1 跟随质点 0 运动,但步调要 稍落后一些,同样质点 1 又推质点 2,使质点 2 也跟随质点 1 运动,但步调又稍落后于质点 1,质点 2 又推质点 3,.,经 1/4 周期,如图 15-5(b)所示,质点 0 到达正向最大偏离 位置,质点 1,2 依次也向各自的正向运动,但依次滞后,质点 3 则要开始移动,质点 3 以 后的质点都没有动。 质点 0 到达正向最大偏离位置便回头向平衡位置移动,这时质点 0 和质点 1 之间因距离 拉开,而相互之间出现拉力,质点 1 拉质点 0,是阻力,质点 0 拉质点 1 是促使质点 1 跟随 质点 0 向负方向移动,经过 1/4 周期,如图 15-5(c)所示,质点 0 正好到达平衡位置,正 朝负方向移动,质点 1 也朝负方向移动,但还未到达平衡位置,仍偏在正的一边,质点 2 又滞后一些,也偏在正的一边,质点 3 刚到达正向最大偏离位置,质点 4,5 也朝正向移动, 但依次滞后一些,质点 6 刚要开始向正向移动。又经过 1/4 周期,各质点的位置如图 15-5 (d)所示。这时质点 6 到达正向最大偏离位置,质点 9 刚要开始向正向移动,再经 1/4 周 期,各质点位置如图 15-5(e)所示,质点 0 回到平衡位置,质点 3 到负向最大偏离位置, 质点 6 到达平衡位置正要向负方向继续移动,质点 9 到达正向最大偏离位置,刚要回头,质 点 12 将要向正方向移动。到 5/4 周期时 ,如图 15-5(f)所示。质点 0 又到达正向最大偏 离位置,质点 3 到达平衡位置,质点 6 到达负向 最大偏离位置,质点 9 到达平衡位置,质 点 12 到达正向最大偏离位置,质点 15 将要向正向移动。 由于质点作纵向运动,介质中便出现疏部与密部,质点 0 完成一次振动,即从图 15-5 (a)到(e),介质里出现一个疏部和一个密部,即出现一个波。质点 0 继续不断地振动, 介质里就 出现一个接一个的传播着的疏部和密部,这就形成了介质中的纵波或者叫疏密波。 5.1.3、波阵面和波射线 一维波的描述相对地比较简单,但对于空间波的描述相对地说就比较复杂一些。因此有必 要采用变通的办法,即采用波面、波前和波射线这些概念,就会变得比较方便,而且图像也 比较清晰。 波阵面 ... 振动周相相同的各点连成的曲面称为波阵面,又叫同相面或简称波面。 波前.. 最前面的(或者说领先的)波阵面称为波前。 波射线 ... 波的传播方向称为波射线或波线。在各向同性介质中,波线总是垂直于波面的。 依照波面的形状不同,来区别二种不同的空间波。它们都是最重要的而且具有代表性的 空间波。 球面波 ... 波面为球形的波,它是由点状波源在各向同性介质中发出的波

(a)球面波 (b)较远处的球面波 (c)平面波 图116空间波 平面波波面为平面的波。通常把从很远处传来的球面波说成是平面波,因为此时的波 面己近似为平面了。 四、播的传播速度 波速也即周相传播的速度,或者就叫做相速。 固体介质里横波的波速=侣,式中n是固体介质的剪切模量,这种模量标志介质剪 切弹性的强弱,P是介质的体密度,固体介质里的横波也是无色散波 至于困体介质里横波的相速、波长、频率、周期之间的关系与绳上波的情形相同,可见 (15-2)式。 液体和气体都是流体,无剪切弹性,自然不能传播横波。 理论研究指出弹性介质里的纵波的波速(即相速)为。一片,式中y是介质的杨氏模 量,它标志介质的张变弹性的强弱,是介质的密度。可见弹性介质里的纵波也是无色散波。 声波是一种级流,其频率从162000,对于空气中的声波,其相速度为。-巴 式中P是气体压强,p是气体密度,y是气体定压比热与定容比热之比值。 波长两个相邻波峰之间(或两个相邻波谷之间)的距离,实际上也就是相邻两同周相点之 间的距离,记作元. 在振动传播着的波里,各个质点振动的频率都一样,这个频率就是波的频率,记作了各 个质点的振动周期也就是波的周期,记作了=了· 波长、波速、频率和周期之间的关系是m=子=。 绳上的波由于其质点的振动方向与波的传播方向垂直,这种波叫致横波。绳上的波其波 速(即相速)与频率「无关,这种被又称无色散波。 波长记为:,它是两个相邻密部之间的距离,也是两个相邻疏部之间的距离或者两个相
6 (a)球面波 (b)较远处的球面波 (c)平面波 图 11-6 空间波 平面波 ... 波面为平面的波。通常把从很远处传来的球面波说成是平面波,因为此时的波 面已近似为平面了。 四、播的传播速度 波速也即周相传播的速度,或者就叫做相速。 固体介质里横波的波速 n v相 = ,式中 n 是固体介质的剪切模量,这种模量标志介质剪 切弹性的强弱, 是介质的体密度,固体介质里的横波也是无色散波。 至于固体介质里横波的相速、波长、频率、周期之间的关系与绳上波的情形相同,可见 (15-2)式。 液体和气体都是流体,无剪切弹性,自然不能传播横波。 理论研究指出弹性介质里的纵波的波速(即相速)为 y v相 = ,式中 y 是介质的杨氏模 量,它标志介质的张变弹性的强弱, 是介质的密度。可见弹性介质里的纵波也是无色散波。 声波是一种纵波,其频率从 16-20 000Hz,对于空气中的声波,其相速度为 p v相 = , 式中 p 是气体压强, 是气体密度, 是气体定压比热与定容比热之比值。 五、波长和频率 波峰.. 质点恰好到达正向最大偏离的位置点。波谷.. 质点恰好到达负向最大偏离的位置点。 波长.. 两个相邻波峰之间(或两个相邻波谷之间)的距离,实际上也就是相邻两同周相点之 间的距离,记作 . 在振动传播着的波里,各个质点振动的频率都一样,这个频率就是波的频率,记作 f, 各 个质点的振动周期也就是波的周期,记作 f T 1 = . 波长、波速、频率和周期之间的关系是 f T v 相 = = . 绳上的波由于其质点的振动方向与波的传播方向垂直,这种波叫做横波。绳上的波其波 速(即相速)与频率 f 无关,这种波又称无色散波。 波长记为 ,它是两个相邻密部之间的距离,也是两个相邻疏部之间的距离或者两个相

邻同相点之间的距离。 波速、波长、频率和周期之间的关系也像绳上波的情形。=子=衫。 5.1.4平面简谐波 5.1.6描述波动的几个物理量 波是振动的传播,如果知道了介质中某一点处(例如,波源,以其平衡位置为原点x0) 的振动情形为叫=ACos1,这一振动传播时,其他质点的振动频率必定与波源相同,假定 无能量损耗,各个质点振动的振幅也都等于A,但各个质点的振动步调不一致,而是依次 滞后,滞后的时间就是振动传到该质点时所需的时间,同时假设沿x正向传播,当波从波源 (在原点处)传播到平衡位置为的那个质点时,所需时间为。,这也就是该质点的振 动滞后于波源报动的时间于是把356式中的时间换成(一藏得到平衡位置为 的质点的振动为 wx,)=Acoso(t-), 式(35-7)表示振动在介质中沿x正向传播时,各点的位移是随平衡位置x和随时间1(它 是自变量)变化的,(35-7)式便是沿x正向传播的波的解析表示式。波的解析表示式还可 以有其他的形式,即 0=cos-之=Aco2n吃-克, 表明振动在介质中沿x正向传播时,各点振动的周相取决于二个因素,即一方面,随时间 1的增大而增大,即每经历一个周期,周相增加2π,当经历1时后,周相便增加红这与地 点x无关。另一方面又随地点x而变化,由原点起波源的振动状态沿x正向传播时,每经过 个波长2的距离周相滞后2,传到x处,周相滞后2π子,这正反映了波在介质中传播, 网相依次滞后的事实。二个方面结合起来看,在x处的振动周相便是2宁一克. 每经历-一个单位时间,周相增加子-2可=®此即圆频率。 每经过一个单位距离,周相滞后红=k,称为波矢量,简称波矢。 于是沿x正向传播的波的解析表示式又可改写为 Mx,)=Acos@-k. 如果描写的是沿x负指向传播的波,这时x处的振动跟原点处的振动相比是超前了 一,因此相应的波的解新表示式应该是 >
7 邻同相点之间的距离。 波速、波长、频率和周期之间的关系也像绳上波的情形。 f T v 相 = = . 5.1.4 平面简谐波 5.1.6 描述波动的几个物理量 波是振动的传播,如果知道了介质中某一点处(例如,波源,以其平衡位置为原点 x=0) 的振动情形为 u A t x=0= cos ,这一振动传播时,其他质点的振动频率必定与波源相同,假定 无能量损耗,各个质点振动的 振幅也都等于 A,但各个质点的振动步调不一致,而是依次 滞后,滞后的时间就是振动传到该质点时所需的时间,同时假设沿 x 正向传播,当波从波源 (在原点处)传播到平衡位置为 x 的那个质点时,所需时间为 x / v相 ,这也就是该质点的振 动滞后于波源振动的时间,于是把(35-6)式中的时间 t 换成( v相 x t − ),就得到平衡位置为 x 的质点的振动为 ( , ) cos ( ) v相 x u x t = A t − , 式(35-7)表示振动在介质中沿 x 正向传播时,各点的位移是随平衡位置 x 和随时间 t(它 是自变量)变化的,(35-7)式便是沿 x 正向传播的波的解析表示式。波的解析表示式还可 以有其他的形式,即 ( ) cos2 ( ) 2 ( , ) cos x T t A v x t T u x t A − = − = 相 , 表明振动在介质中沿 x 正向传播时,各点振动的周相取决于二个因素,即一方面, 随时间 t 的增大而增大,即每经历一个周期,周相增加 2 ,当经历 t 时后,周相便增加 t T 2 这与地 点 x 无关。另一方面又随地点 x 而变化,由原点起波源的振动状态沿 x 正向传播时,每经过 一个波长 的距离周相滞后 2 ,传到 x 处,周相滞后 x 2 ,这正反映了波在介质中传播, 周相依次滞后的事实。二个方面结合起来看,在 x 处的振动周相便是 2 ( ) x T t − . 每经历一个单位时间,周相增加 = = f T 2 2 此即圆频率。 每经过一个单位距离,周相滞后 = k 2 ,称为波矢量,简称波矢。 于是沿 x 正向传播的波的解析表示式又可改写为 u(x,t) = Acos(t −kx) . 如果描写的是沿 x 负指向传播的波,这时 x 处的振动跟原点处的振动相比是超前了 v相 x ,因此相应的波的解析表示式应该是

Mx)=4co0t+,0=4cos2号+克,x)=4cose1+k. 对于球面波的描述,由于随者离波源距离r的增加,波面面积随增加,因此考虑到能 量越来越分散,其波强7与距离平方成反比,而与振幅?成正比的关系,如果以r-1米处 的振幅为4时,r处的振幅便为A=4由此可见球面波的解析表达式为 ==4c0so-k 波动表式的意义: 上式代表处质点在其平衡位置附近以角颜率W作简谐云动0一,一 1、x一定。令x-x1,则质点位移y仅是时间1的函数。v= 2、1一定。令=1,则质点位移y仅是x的函数。 2πx y=Acos@- 以y为纵坐标、x为横坐标,得到一条余弦曲线,它是1时刻波线上各个质点偏离各自 平衡位置的位移所构成的波形曲线(波形图)。 沿波线方向,任意两点、?的简谐运动相位差为: 3、1都变化。4p=%-%=-2r55-2x 实线:1时刻波形:虚线:2时刻波形 当1时,y=Ac0a-+%] 当=1+1时 y=4o时o+-+% 在1和1+△1时刻,对应的位移用)和2表示,则 令x2)=1+u△1,得 在△1时间内,整个波形向波的传播方向移动了△x=x2xI)=u△6,波速M是整个波形向
8 ( , ) cos ( ) v相 x u x t = A t + , ( , ) cos2 ( ) x T t u x t = A + ,u(x, t) = Acos(t + kx) . 对于球面波的描述,由于随着离波源距离 r 的增加,波面面积随 2 r 增加,因此考虑到能 量越来越分散,其波强 I 与距离平方成反比,而与振幅 2 A 成正比的关系,如果以 r=1 米处 的振幅为 A0 时,r 处的振幅便为 0 1 A r A = 由此可见球面波的解析表达式为 cos( ) 1 ( ) 0 A t k r r u = u r = − . 波动表式的意义: 1、x 一定。令 x=x1,则质点位移 y 仅是时间 t 的函数。 上式代表 x1 处质点在其平衡位置附近以角频率 w 作简谐运动 2、t 一定。令 t=t1,则质点位移 y 仅是 x 的函数。 以 y 为纵坐标、x 为横坐标,得到一条余弦曲线,它是 t1 时刻波线上各个质点偏离各自 平衡位置的位移所构成的波形曲线(波形图)。 沿波线方向,任意两点 x1、x2 的简谐运动相位差为: 3、x、t 都变化。 实线:t1 时刻波形;虚线:t2 时刻波形 当 t=t1 时, 当 t= t1+Δt 时 在 t1 和 t1+Δt 时刻,对应的位移用 x(1) 和 x(2)表示,则 令 x(2)=x(1)+uΔt,得 在Δt 时间内,整个波形向波的传播方向移动了Δx=x(2)-x(1)=uΔt,波速 u 是整个波形向 = − 2 1 cos x y A t = − x y A t 2 cos 1 x x x = − − = − = −2 2 2 1 2 1 x y u x=u t 波的传播 + = 1 − 0 cos u x y A t + = 1 + − 0 cos u x y A t t + = − 0 (1) ( ) 1 cos 1 u x y A t t + + = + − 0 (2) ( ) 1 cos 1 u x y A t t t t + + + = + − 0 (1) ( ) 1 cos 1 u x u t y A t t t t 0 ( ) (1) 1 1 cos t y u x A t = + = −

前传播的速度。 波速“有时也称相速度, 5.2平面简谐波的波动方程 对 y=Acos[ol-x)+真]求x、1的二阶偏导数得到 2-om-} -gm-} 0x2 任何物理量y,若它与时间、坐标间的关系满足上式,则这一物理量就按波的形式传播。 在三维空间中的一切波动过程,只要介质无吸收且各向同性,都适合下式: 18E 5代表振动位移 球面波的波动方程: Or u2 812 球面波的余弦表式如下: r()=4cos(ot+kr) ar—振幅 例题163频率为125k五的平面余弦纵波沿细长的金属捧传播,棒的杨氏模量为 =1.9x1011N/m2,棒的密度p=7.6x103kgm3。如以棒上某点取为坐标原点,已知原点处质 点振动的振幅为A=1mm,试求:(1)原点处质点的振动表式,(2波动表式,(3)离原点10cm 处质点的振动表式,(4)离原点20cm和30cm两点处质点振动的相位差,(5)在原点振动 0.0021s时的波形。 解棒中的波速 w= Vp76x1=50x10'm/s 1.9×10N.m2 ="_5.0×103ms -=0.40m 12.5×10s ()原点处质点的振动表式 w=Acos00.1×10-3cos(2×π12.5x1031)m=0.1x10r3cos25×103π1m T=1/y=8×10-5s
9 前传播的速度。 波速 u 有时也称相速度。 5.2 平面简谐波的波动方程 对 求 x 、t 的二阶偏导数,得到 任何物理量 y ,若它与时间、坐标间的关系满足上式,则这一物理量就按波的形式传播。 在三维空间中的一切波动过程,只要介质无吸收且各向同性,都适合下式: 代表振动位移。 球面波的波动方程: 球面波的余弦表式如下: ( ) cos( t kr) r a r t = + a/r——振幅 例题 16-3 频率为 =12.5kHz 的平面余弦纵波沿细长的金属棒传播,棒的杨氏模量为 Y =1.91011N/m2,棒的密度 =7.6103kg/m3。如以棒上某点取为坐标原点,已知原点处质 点振动的振幅为 A =0.1mm,试求:(1)原点处质点的振动表式,(2)波动表式,(3)离原点 10cm 处质点的振动表式,(4)离原点 20cm 和 30cm 两点处质点振动的相位差,(5)在原点振动 0.0021s 时的波形。 解 棒中的波速 (1)原点处质点的振动表式 y0=Acos t=0.110-3 cos(212.5103 t)m=0.110-3 cos25103tm ( ) 0 y = Acos t − x u + cos , 0 2 2 2 + = − − u x A t t y cos , 2 0 2 2 2 + = − − u x t u A x y 2 2 2 2 2 1 t y x u y = 2 2 2 2 2 2 2 2 2 1 x y z u t = + + 2 2 2 2 2 ( ) 1 ( ) t r r u r = + = − 0 cos u r t r a 5.0 10 m/s 7.6 10 kg m 1.9 10 N m 3 3 3 11 2 = = = − − Y u 0.40m 12.5 10 s 5.0 10 m s 3 1 3 1 = = = − − v u 1 8 10 s −5 T = v =
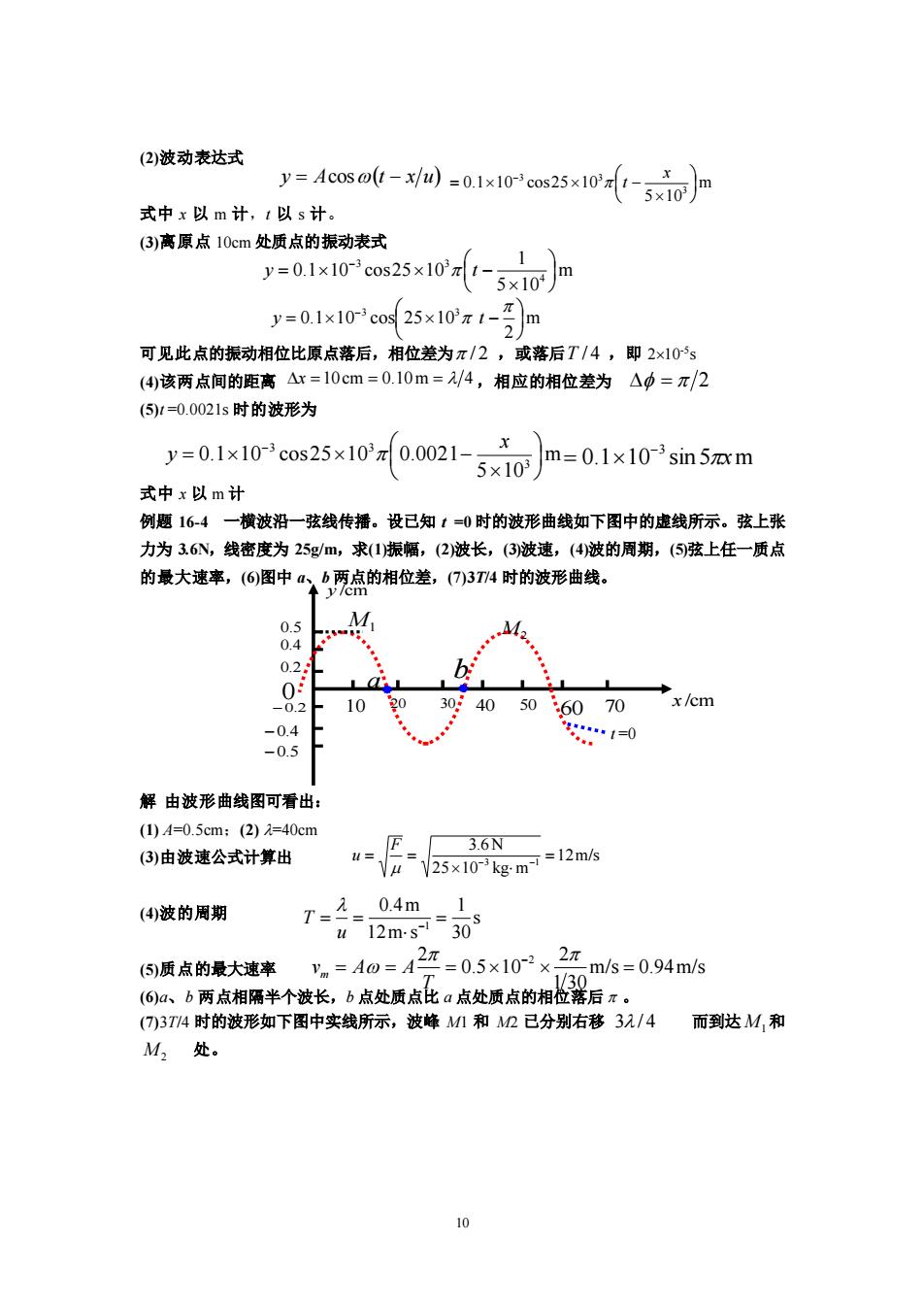
(2)波动表达式 y=Acos)01xosx1)m 式中x以m计,1以s计。 (3)离原点10cm处质点的振动表式 y=0.1x10cos25x10-3x10m 1 y=0.1x103cos25x10x1-m 可见此点的振动相位比原点落后,相位差为π/2,或落后T/4,即2×10s (4该两点间的距离r=10cm=0.10m=4,相应的相位差为△中=π/2 (⑤1=0.0021s时的波形为 y=0.1x10'cos25x100.0021-5x10m=0.1×103sin5am X 式中x以m计 例题164一横波沿一弦线传播。设已知1=0时的波形曲线如下图中的虚线所示。弦上张 力为36N,线密度为25gm,求1振幅,(2波长,(③波速,(4波的周期,(5弦上任一质点 的最大速率,(O图中ab两点的相位差,(7)3T4时的波形曲线。 0.5 M 0.4 0.2 0 10 30 4050 6070 x/cm -0.4 .1=0 -0.5 解由波形曲线图可看出: (1)A=0.5cm:(2)i=40cm (3)由波速公式计算出 3.6N M= 25x 10 kg m2m/s (4波的周期 (⑤)质点的最大速率 Vm=A0= 42==05×102×2 m/s=0.94m/s (6a、b两点相隔半个波长,b点处质点比a点处质点的相位落后π。 (T)3T4时的波形如下图中实线所示,波峰M1和M2已分别右移31/4而到达M,和 M2处
10 (2)波动表达式 式中 x 以 m 计,t 以 s 计。 (3)离原点 10cm 处质点的振动表式 可见此点的振动相位比原点落后,相位差为 / 2 ,或落后 T / 4 ,即 210-5 s (4)该两点间的距离 ,相应的相位差为 (5)t =0.0021s 时的波形为 式中 x 以 m 计 例题 16-4 一横波沿一弦线传播。设已知 t =0 时的波形曲线如下图中的虚线所示。弦上张 力为 3.6N,线密度为 25g/m,求(1)振幅,(2)波长,(3)波速,(4)波的周期,(5)弦上任一质点 的最大速率,(6)图中 a、b 两点的相位差,(7)3T/4 时的波形曲线。 解 由波形曲线图可看出: (1) A=0.5cm;(2) =40cm (3)由波速公式计算出 (4)波的周期 (5)质点的最大速率 (6)a、b 两点相隔半个波长,b 点处质点比 a 点处质点的相位落后 。 (7)3T/4 时的波形如下图中实线所示,波峰 M1 和 M2 已分别右移 3 / 4 而到达 M1 和 M2 处。 y = Acos(t − x u) m 5 10 0.1 10 cos25 10 3 3 3 = − − x t m 5 10 1 0.1 0 cos25 10 4 3 3 = − − y t m 2 0.1 10 cos 25 10 3 3 = − − y t x = 10cm = 0.10m = 4 = 2 m 5 10 0.1 10 cos25 10 0.0021 3 3 3 = − − x y 0.1 10 sin 5 m 3 x − = x /cm y /cm 0.4 −0.2 −0.4 −0.5 M1 M2 0.5 0.2 0 10 20 30 40 50 60 70 a b t =0 12m/s 25 10 kg m 3.6N 3 1 = = = − − F u s 30 1 12m s 0.4m 1 = = = − u T m/s 0.94m/s 1 30 2 0.5 10 2 2 = = = = − T vm A A