
塞曼效应 石河子大学物理系近代物理实验课程组 20142015第一学期
塞 曼 效 应 石河子大学物理系近代物理实验课程组 2014-2015第一学期

■一、 背景介绍 二、 实验目的 三、实验原理 ▣四、 实验仪器 五、实验内容与步骤 ■ 六、注意事项 ·七、思考题
一、背景介绍 二、实验目的 三、实验原理 四、实验仪器 五、实验内容与步骤 六、注意事项 七、思考题

一、背景介绍 1896年开始,塞曼逐步发现,当光源 放在足够强的磁场中时,所发出的光谱线分 裂成若干条。条数随能级的类别而不同。而 分裂后的谱线成份是偏振的。这种现象称为 塞曼效应
一、背景介绍 1896年开始,塞曼逐步发现,当光源 放在足够强的磁场中时,所发出的光谱线分 裂成若干条。条数随能级的类别而不同。而 分裂后的谱线成份是偏振的。这种现象称为 塞曼效应

塞曼研究磁场对光谱的作用,是受著名 英国物理学家法拉第的启示。 NBS 塞曼(Pieter Zeeman)1865~1943 诺贝尔物理学奖(1902年)
➢ 塞曼研究磁场对光谱的作用,是受著名 英国物理学家法拉第的启示。 塞曼( Pieter Zeeman ) 1865~1943 诺贝尔物理学奖 (1902年)

1845年法拉第发现了平面偏振光通过在 强磁场作用下的玻璃偏振面会旋转的事实。 后来又发现,不只是玻璃,许多物质都具有 这一特性。法拉第认为:“磁力和光彼此是 有联系的。” 1875年,物理学家John kerr?在法拉第思想的 激励下,注意到玻璃片在强电场下对光有双 折射作用,次年又发现平面偏振光经电磁铁 的磁极反射后,变成了椭圆偏振光
1845年法拉第发现了平面偏振光通过在 强磁场作用下的玻璃偏振面会旋转的事实。 后来又发现,不只是玻璃,许多物质都具有 这一特性。法拉第认为:“磁力和光彼此是 有联系的。” 1875年,物理学家John kerr在法拉第思想的 激励下,注意到玻璃片在强电场下对光有双 折射作用,次年又发现平面偏振光经电磁铁 的磁极反射后,变成了椭圆偏振光

1895年前后,塞曼放下ke11效应的研究,想试一试磁场 对钠焰的光谱有没有影响,却都没成功但他坚持作了下去。 他根据法拉第的想法,用罗兰凹面光栅和强大的电磁铁, 发现钠黄线在磁场的作用下变宽,后来又观察到镉兰线在磁 场的作用下分裂成两根与三根;不久洛仑兹根据经典电子论 解释了分裂为三条的正常塞曼效应。这一发现引起了很多物 理学家开展广泛研究,然而,大多数情况却与经典电子论的 理论结果不符,这叫反常塞曼效应。促使1921年朗德提出g因 子概念,1925年泡利提出不相容原理,同年乌伦贝克和哥德 斯密特提出电子自旋,从而推动量子理论的发展。 塞曼效应证实了原子具有磁距和空间量子化,至今仍是 研究能级结构的重要方法之一
1895年前后,塞曼放下kell效应的研究,想试一试磁场 对钠焰的光谱有没有影响,却都没成功但他坚持作了下去。 他根据法拉第的想法,用罗兰凹面光栅和强大的电磁铁, 发现钠黄线在磁场的作用下变宽,后来又观察到镉兰线在磁 场的作用下分裂成两根与三根;不久洛仑兹根据经典电子论 解释了分裂为三条的正常塞曼效应。这一发现引起了很多物 理学家开展广泛研究,然而,大多数情况却与经典电子论的 理论结果不符,这叫反常塞曼效应。促使1921年朗德提出g因 子概念,1925年泡利提出不相容原理,同年乌伦贝克和哥德 斯密特提出电子自旋,从而推动量子理论的发展。 塞曼效应证实了原子具有磁距和空间量子化,至今仍是 研究能级结构的重要方法之一

二、实验目的 1、观察汞的546.074nm谱线在磁场中分裂 的情况,加深对原子结构的认识: 2、测量上述谱线在磁场中分裂的裂距,求 出e/m值; 3、学习法布里一珀罗标准具的原理、调 节和使用
二、实验目的 1、观察汞的546.074nm谱线在磁场中分裂 的情况,加深对原子结构的认识; 2、测量上述谱线在磁场中分裂的裂距,求 出e/m值; 3、学习法布里——珀罗标准具的原理、调 节和使用

三、实验原理 塞曼效应是由于电子的轨道磁矩与自旋磁矩共同受 外磁场的作用而产生的。 电子从高能级向低能级跃迁时会发光。一定的光谱 线对应于一定的能级间的跃迁。例如汞的 546.074nm谱线是6S7S3S1到6S6P3P2跃迁的结果。 谱线在磁场中分裂这一事实,反映了能级在磁场中 发生了分裂,也即原子在磁场中获得了附加能量。 ▣运用量子力学。可以对塞曼效应作出满意的解释
三、实验原理 塞曼效应是由于电子的轨道磁矩与自旋磁矩共同受 外磁场的作用而产生的。 电子从高能级向低能级跃迁时会发光。一定的光谱 线对应于一定的能级间的跃迁。例如汞的 546.074nm谱线是6S7S³Sı到6S6P³P2跃迁的结果。 谱线在磁场中分裂这一事实,反映了能级在磁场中 发生了分裂,也即原子在磁场中获得了附加能量。 运用量子力学。可以对塞曼效应作出满意的解释
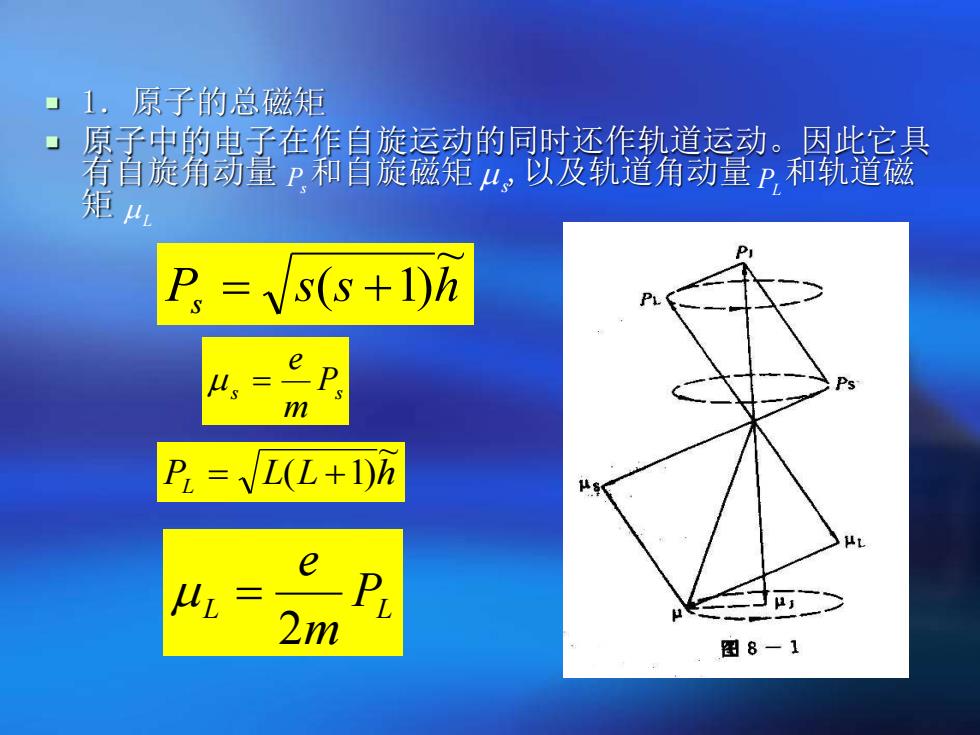
1,原子的总磁矩 原子中的电子在作自旋运动的同时还作轨道运动。因此它具 有 自旋角动量P和自旋磁矩4,以及轨道角动量P和轨道磁 矩4 =s(s+1)h 山。= m P=√L(L+1)h 2m 图8-1
1.原子的总磁矩 原子中的电子在作自旋运动的同时还作轨道运动。因此它具 有自旋角动量 和自旋磁矩 ,以及轨道角动量 和轨道磁 矩 Ps s s h ~ = ( +1) s Ps m e = PL L L h ~ = ( +1) L PL m e 2 = Ps s PL L

总磁矩“则是4与弘,的合成。由于4,与的比值不同于用的 比值,所μ不在总角动量的延长线上。但是,P耶都是绕 着旋进的,因此、4和也都是绕着的延长线旋进的。如 果把分解成方向在钯,延长线的分量弘和与之垂直的另外一 个分量,则后者在绕?转动时,对外的平均效果完全抵消。这 样,对外发生效果的只是。因此,人们就将称之为“原子 总磁矩” ■进行矢量迭加运算后得: 4=8 2m ▣.其中的g称为朗德因子。对于LS耦合 J(J+1)-L(L+1)+S(S+1) J(J+1) =S+L 所以只要知道原子态性质,就可以算出原子总磁矩;反之,从 对原子磁性的研究,也可以提供有关原子态的线索
总磁矩 则是 与 的合成。由于 与 的比值不同于 与 的 比值,所以 不在总角动量 的延长线上。但是, 和 都是绕 着 旋进的,因此 、 和 也都是绕着 的延长线旋进的。如 果把 分解成方向在 延长线的分量 和与之垂直的另外一 个分量,则后者在绕 转动时,对外的平均效果完全抵消。这 样,对外发生效果的只是 。因此,人们就将 称之为“原子 总磁矩”。 进行矢量迭加运算后得: 其中的g称为朗德因子。对于LS耦合 所以只要知道原子态性质,就可以算出原子总磁矩;反之,从 对原子磁性的研究,也可以提供有关原子态的线索。 j Pj m e g 2 = 1 ( 1) ( 1) ( 1) ( 1) + + + − + + + = sJ J J J L L S S g J = S + L s L s Ps L PJ PL PJ s L PJ PJ J PJ J J PL Ps