
验证快速电子的动量与动能的相对论关系 >实验且的 >实验背景 >实验原理 >实验步骤 >数据处理 >注意事项 >实验扩展 石河子大学物理系近代物理实验课程组 2014-2015第一学期
验证快速电子的动量与动能的相对论关系 ➢实验目的 ➢实验背景 ➢实验原理 ➢实验步骤 ➢数据处理 ➢注意事项 ➢实验扩展 石河子大学物理系近代物理实验课程组 2014-2015第一学期

验证快速电子的动量与动能的相对论关系 实验目的 本实验通过对快速电子的动量值及动能的 同时测定来验证动量和动能之间的相对论关系。 同时实验者将从中学习到B磁谱仪测量原理、 闪烁记数器的使用方法及一些实验数据处理的 思想方法。 返回目录
验证快速电子的动量与动能的相对论关系 ❖实验目的 本实验通过对快速电子的动量值及动能的 同时测定来验证动量和动能之间的相对论关系。 同时实验者将从中学习到 磁谱仪测量原理、 闪烁记数器的使用方法及一些实验数据处理的 思想方法。 返回目录

验证快速电子的动量与动能的相对论关系 实验背景 牛顿的绝对时空观认为时间和空间是两个独立的概念,彼此 之间没有联系;同一物体在不同惯性参照系中观察到的运动学量 可通过伽利略变换而互相联系。这就是力学相对性原理:一切力 学规律在伽利略变换下是不变的。 19世纪末至20世纪初,人们试图将伽利略变换和力学相对性 原理推广到电磁学和光学时遇到了困难。实验证明对高速运动的 物体伽利略变换是不正确的,实验还证明在所有惯性参照系中光 在真空中的传播速度为同一常数。 在此基础上,爱因斯坦于1905年提出了狭义相对论,并据此 导出从一个惯性系到另一个惯性系的变换方程即“洛伦兹变换”。 返回日录
验证快速电子的动量与动能的相对论关系 ❖实验背景 牛顿的绝对时空观认为时间和空间是两个独立的概念,彼此 之间没有联系;同一物体在不同惯性参照系中观察到的运动学量 可通过伽利略变换而互相联系。这就是力学相对性原理:一切力 学规律在伽利略变换下是不变的。 19世纪末至20世纪初,人们试图将伽利略变换和力学相对性 原理推广到电磁学和光学时遇到了困难。实验证明对高速运动的 物体伽利略变换是不正确的,实验还证明在所有惯性参照系中光 在真空中的传播速度为同一常数。 在此基础上,爱因斯坦于1905年提出了狭义相对论,并据此 导出从一个惯性系到另一个惯性系的变换方程即“洛伦兹变换”。 返回目录
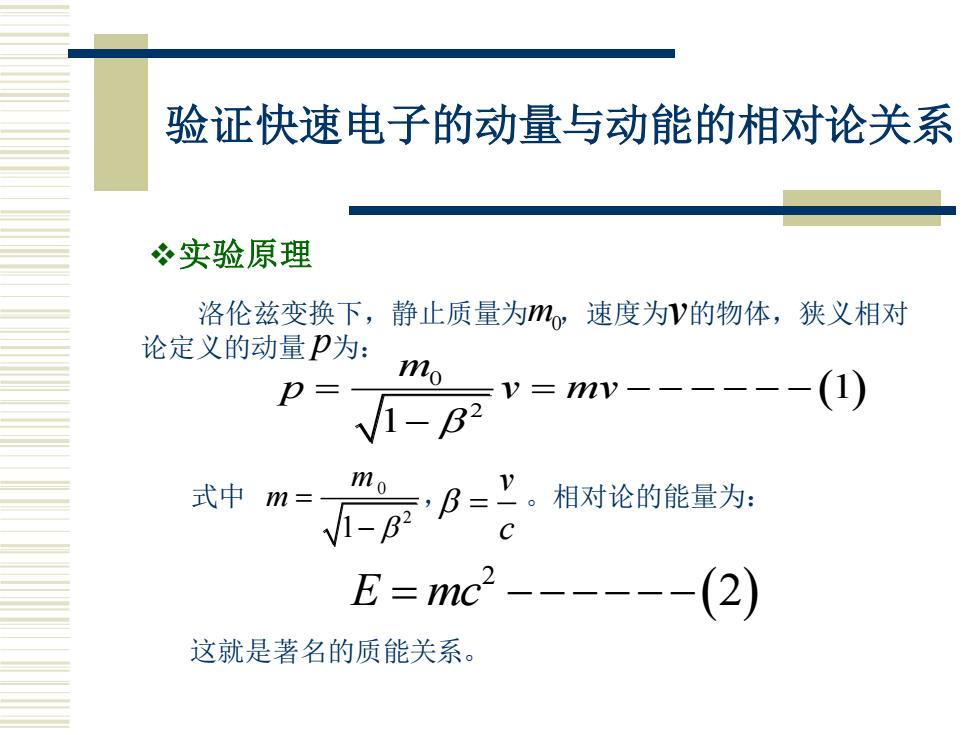
验证快速电子的动量与动能的相对论关系 实验原理 洛伦兹变换下,静止质量为mo,速度为V的物体,狭义相对 论定义的动量P为: mo p v=mv- (1) V√1-B2 式中 m= mo B=上。相对论的能量为 C E=mc- 2 这就是著名的质能关系
验证快速电子的动量与动能的相对论关系 ❖实验原理 洛伦兹变换下,静止质量为 ,速度为 的物体,狭义相对 论定义的动量 为: m0 v p ( ) 0 2 1 1 m p v mv = = − − − − − − − 式中 0 , 。相对论的能量为: 2 1 m m = − v c = ( ) 2 E mc = − − − − − − 2 这就是著名的质能关系

验证快速电子的动量与动能的相对论关系 冬实验原理 由(1)式和(2)式可得:E2=c2p2+E 其中E。=m,c为静止质量。 物体的动能为: E6=E-E。=Vcp2+m,2c4-m,c2- (3 这就是我们要验证的狭义相对论的动量与动能的关系
验证快速电子的动量与动能的相对论关系 ❖实验原理 由(1)式和(2)式可得: 2 2 2 2 E c p E = + 0 其中 为静止质量。 2 E m c 0 0 = 物体的动能为: 2 2 2 4 2 0 0 0 (3) E E E c p m c m c k = − = + − − − − − − − 这就是我们要验证的狭义相对论的动量与动能的关系
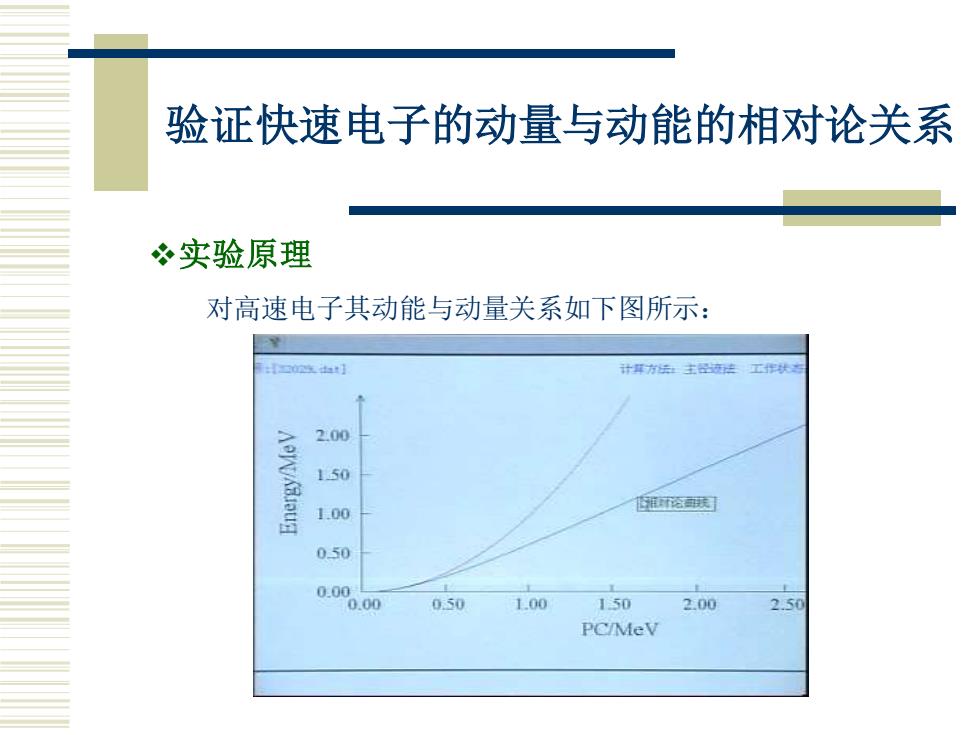
验证快速电子的动量与动能的相对论关系 实验原理 对高速电子其动能与动量关系如下图所示: 计耳方法士出法工示作状 200 150 1.00 湘诊肤 050 0.0 0.00 0.50 1.00 150 2.00 PC/MeV
验证快速电子的动量与动能的相对论关系 ❖实验原理 对高速电子其动能与动量关系如下图所示:

验证快速电子的动量与动能的相对论关系 冬实验原理 天-wa百 当B<<1时, 2 mo 电子的mc2=0.511MeV,上式可化为: 1p2c2 P'c2 2m,c2 2×0.511 以利于计算
验证快速电子的动量与动能的相对论关系 ❖实验原理 物体的动能也可以写成: 2 2 2 0 0 2 1 1 1 E mc m c m c k = − = − − 当 <<1时, 2 2 2 2 2 2 0 0 0 1 1 1 1 2 2 2 k v p E mc m c m v c m = + + − = 电子的 ,上式可化为: 2 0 m c MeV = 0.511 2 2 2 2 2 0 1 2 2 0.511 k p c p c E m c = = 以利于计算。

验证快速电子的动量与动能的相对论关系 实验原理 验证相对论效应实验装置及其示意图如下: →有应源 其度盒 均匀独功 插基一 电哪
验证快速电子的动量与动能的相对论关系 ❖实验原理 验证相对论效应实验装置及其示意图如下:

验证快速电子的动量与动能的相对论关系 实验原理 B源射出的高速B粒子经准直后垂直射入一均匀磁场中, 粒子因受到与运动方向垂直的洛伦兹力的作用而作圆周运动。 如果认为在空气中其能量的损失很小,则粒子具有恒定的动量 数值,仅仅是方向不断变化,这一确定的动量值为: p=eBR 式中e为电子电荷,B为磁场强度,R为粒子轨道半径
验证快速电子的动量与动能的相对论关系 ❖实验原理 源射出的高速 粒子经准直后垂直射入一均匀磁场中, 粒子因受到与运动方向垂直的洛伦兹力的作用而作圆周运动。 如果认为在空气中其能量的损失很小,则粒子具有恒定的动量 数值,仅仅是方向不断变化,这一确定的动量值为: p eBR = 式中 e 为电子电荷, B 为磁场强度, R 为粒子轨道半径

验证快速电子的动量与动能的相对论关系 实验原理 在磁场外距B源恥X处放置一个B能量探测器来接收从该 处出射的B粒子,则这些粒子的能量(即动能)可由探测器 直接测出,而粒子的动量值即为: p=eBR=eBAX/2 由于B源射出的B粒子具有连续的能量分布,因此探 测器在不同位置就可以测得一系列不同的能量与对应的动量 值。这样就可以用实验方法确定测量范围内动能与动量的对 应关系,进而验证相对论给出的这一关系的理论公式的正确 性。 返回且录
验证快速电子的动量与动能的相对论关系 ❖实验原理 在磁场外距 源 处放置一个 能量探测器来接收从该 处出射的 粒子,则这些粒子的能量(即动能)可由探测器 直接测出,而粒子的动量值即为: X p eBR eB X = = / 2 由于 源射出的 粒子具有连续的能量分布,因此探 测器在不同位置就可以测得一系列不同的能量与对应的动量 值。这样就可以用实验方法确定测量范围内动能与动量的对 应关系,进而验证相对论给出的这一关系的理论公式的正确 性。 返回目录