
第四章机械振动 引言: 1.振动的概念 (1)机械振动 物体在一定的位置附近所作的来回往复的运动称为机械根动。如:摆、发声体等。 (2)广义振动概念 凡是描写运动状态的物理量,在某一数值附近作周期性的变化,都叫做振动。 例如:交流电压、电流的变化、无线电波电磁场的变化等等。 2.本章内容 简谐振动、阻尼振动、受迫振动*、共振*等。 4.1简谐振动的动力学特征 4.1.1弹簧振子模型 1.简谐振动的概念 物体运动时,如果离开平衡位置的位移(或角位移)按余 弦函数(或正弦函数)的规律随时间变化,这种运动就叫简诰 jmo 振动。 2.简谐振动及其表达式(运动学方程) 简谐振动的运动方程可写为: x=Acos+): 3.简谐振动物体的速度和加速度 对运动方程求导可得到任意时刻物体振动的速度和加速 度: (1)v==-a4sin@1+p)=.coso1+p+/2, 式中:=a4,a.=a2A,a=-0x 图141简诺振 4.1.2.微振动的简谐近似
第四章 机械振动 引言: 1.振动的概念 (1)机械振动 物体在一定的位置附近所作的来回往复的运动称为机械振动。如:摆、发声体等。 (2)广义振动概念 凡是描写运动状态的物理量,在某一数值附近作周期性的变化,都叫做振动。 例如:交流电压、电流的变化、无线电波电磁场的变化等等. 2.本章内容 简谐振动、阻尼振动、受迫振动*、共振*等。 4.1 简谐振动的动力学特征 4.1.1 弹簧振子模型 1.简谐振动的概念 物体运动时,如果离开平衡位置的位移(或角位移)按余 弦函数(或正弦函数〕的规律随时间变化,这种运动就叫简谐 振动。 2.简谐振动及其表达式(运动学方程) 简谐振动的运动方程可写为: x = Acos( t +) ; 3.简谐振动物体的速度和加速度 对运动方程求导可得到任意时刻物体振动的速度和加速 度: (1) sin( ) cos( / 2) d d = = −A t + = v t + + t x v m , (2) cos( ) cos( ) d d d d 2 2 = = = −A t + = a t + + t x t v a m , 式中: vm = A, am A 2 = , a x 2 = − . 图 14-1 简谐振动 4.1.2.微振动的简谐近似 t x x O O

1、单摆 如图184所示,单摆在小角度摆动时,重力矩作为回复力矩,其大小为mgsn0=g8 由转动定律M=的,则地=-0,又J=m,则=-0,。=民, 【例3】重力加速度变化时,单摆的周期也变化,dTT与dgg之间的关系是 【分桥1T25,则2,g-g 图18-4 2、复摆 一个可绕固定轴摆动的刚体称为复摆 刚体的质心为C,对过0点的转轴的转动惯量为人O、C两点间距离的距离为1。 据转动定律,得 b 0i2g-= 若角度较小时 b Origm- 。0=68+g 1 即 fun 例152一质量为m的平底船,其平均水平截面积为S,吃水深度为,如不计水的阻力 求此船在竖直方向的振动周期。 解:船静止时浮力与重力平衡, ohSg =mg 7☑片 船在任一位置时,以水面为坐标原点,竖直向下的坐标轴为y轴,船的位移用y表示 船的位移为y时船所受合力为: f=-(h+y)pSg+mg=-ypSg 船在竖直方向作简谐振动,其角频率和周期为: 鹰 T2=2% m .m=pSh, :.T=2K18
2 1、 单摆 如图 18-4 所示,单摆在小角度摆动时,重力矩作为回复力矩,其大小为 mglsin mgl , 由转动定律 2 2 d d t M J = ,则 J mgl t J = − 2 2 d d ,又 2 J = ml ,则 l g t = − 2 2 d d , l g = . 【例 3】 重力加速度变化时,单摆的周期也变化,dT/T 与 dg/g 之间的关系是_. 【分析】 g l T = 2 ,则 g g g l T )d 2 1 d = 2 (− , g g T T d ) 2 1 ( d = − . 图 18-4 2、复摆 一个可绕固定轴摆动的刚体称为复摆。 刚体的质心为 C, 对过 O 点的转轴的转动惯量为 J, O、C 两点间距离的距离为 h。 据转动定律,得 若 角度较小时 即 例 15-2 一质量为 m 的平底船,其平均水平截面积为 S,吃水深度为 h,如不计水的阻力, 求此船在竖直方向的振动周期。 解: 船静止时浮力与重力平衡, 船在任一位置时,以水面为坐标原点,竖直向下的坐标轴为 y 轴,船的位移用 y 表示 船的位移为 y 时船所受合力为: 船在竖直方向作简谐振动,其角频率和周期为: sin d d 2 2 mgh t − = J mgh t − = J 2 2 d d J mgh 2 0 d 2 d 2 2 = + t mgh J T 2 2 = = g m C O hSg = mg O y P P y f = −(h + y)Sg + mg = −ySg m Sg = gS m T 2 2 = = m = Sh, g h T = 2

4.2简谐振动运动学 4.2.1简谐振动的运动学方程 简诰振动一般可分为自由简诺振动和受迫简谐振动, 首先介绍自由简谐振动,这类振动是指物体仅受振动系统 内部的恢复力(如弹性力)的作用。当物体离开平衡位置 0x* 到达x位置处,它受的弹性恢复力为:F=-::k为弹簧 的倔强系数。 若设物体质量为m,它在时刻t的加速度,振子所受的摩擦阻力与弹簧的质量均忽略不 计,则由牛顿运动定律得: 令★=心为角频率可得: +=0, 这就是弹簧振子满足的动力学方程,其解为: x=AcosQπ+p) 图142,a-图 4.2.2简谐运动的三个重要参量 现在我们讨论简谐振动运动学方程中的A、。、a1+p的物理意义。 (一)、振幅A 1.平衡位置 任何机械振动的物体都始终徘徊在某一定位置的附近,这个位置称为平衡位置 2.振幅A -A≤x≤4,将物体离开平衡位置的最大位移的绝对值称为振动的振幅。 (二)、周期和频率 1,周期 每隔一个固定的时间,物体的运动状态就完全重复一次。这固定的时间T称为振动的周期。 2.频率
3 4.2 简谐振动运动学 4.2.1 简谐振动的运动学方程 简谐振动一般可分为自由简谐振动和受迫简谐振动, 首先介绍自由简谐振动,这类振动是指物体仅受振动系统 内部的恢复力(如弹性力)的作用。当物体离开平衡位置 到达 x 位置处,它受的弹性恢复力为: F = −k x ;k 为弹簧 的倔强系数。 若设物体质量为m,它在时刻t的加速度 a,振子所受的摩擦阻力与弹簧的质量均忽略不 计,则由牛顿运动定律得: F = −k x = ma , 0 d d 2 2 + x = m k t x , 令 2 = m k 为角频率可得: 0 d d 2 2 2 + x = t x , 这就是弹簧振子满足的动力学方程,其解为: x = Acos(2t +) . 图 14-2 x-t,v-t,a-t 图 4.2.2 简谐运动的三个重要参量 现在我们讨论简谐振动运动学方程中的 A、 、 t + 的物理意义。 (一)、振幅 A 1.平衡位置 任何机械振动的物体都始终徘徊在某一定位置的附近,这个位置称为平衡位置。 2.振幅 A −A x A ,将物体离开平衡位置的最大位移的绝对值称为振动的振幅。 (二)、周期和频率 1.周期 每隔一个固定的时间,物体的运动状态就完全重复一次。这固定的时间 T 称为振动的周期。 2.频率 Ep - A +A x Ek O Ep B E x

每秒内振动的次数称为频率,(出). 3.四、T、v的关系 (1)a、T 注意到+T刀=x0,可得:Acos@t+aT+p)=Acos@1+p). 因此有:o1=2,T=语: 注意到。一,因此有:T限 (2)v、T v=7 (3)m、v 。=2江,。=2因为人。、为粗成简银动的系特征量所定 与外界无关,称为固有周期和固有频率。运动方程也可写为x=Acos2xW+p)或 x=AcosQu/T+). (三)、相位 1.相位p (@1+p)和A、0一起决定1时刻物体运动状态,即位移x,速度y和加速度a, 2。初相决定时刻物体运动状态,即初始位移,初始速度 (四)、由初始条件确定振幅和初相 如果已知初始条件1-0,x-,r-0,代入运动学方程有:名=4cosp,=-m4snp 因此:A=代+(合,p=arctan-点. 讨论:(1)相位的物理意义和现代物理学中地位: (2)运动学方程指数表示. 【例1】一轻弹簧的倔强系数为k,其下悬有一质量为m的盘子,现有一质量为M的物体 从离盘h高度外自由下落到盘中并和盘子粘在一起,于是盘子开始振动。 (1)此时的振动周期与空盘子振动时的周期有何不同? (2)此时的振动振幅多大? (3)取平衡位置为原点,位移以向下为正,并以弹簧开始振动时作为计时起点,求初相, 并写出物体与盘子的振动方程. 【分析】(1)M落到m之前,做自由落体运动,与m作完全非弹性碰撞前的最大速度为
4 每秒内振动的次数称为频率 (HZ). 3. 、T、 的关系 (1) 、T 注意到 x(t +T) = x(t) ,可得: Acos( t +T +) = Acos( t +) . 因此有: T = 2 , = 2 T ; 注意到 m k = ,因此有: k m T = 2 . (2) 、T T 1 = (3) 、 T = 2 , = 2 , m k = 2 1 因为 T、 、 为组成简谐振动的系统特征量所决定, 与外界无关,称为固有周期和固有频率。运动方程也可写为 x = Acos(2t +) 或 x = Acos(2t/T +). (三)、相位 1.相位 (t +) 和 A、 一起决定 t 时刻物体运动状态,即位移 x,速度 v 和加速度 a.. 2.初相决定时刻物体运动状态,即初始位移,初始速度. (四)、由初始条件确定振幅和初相 如果已知初始条件 t=0 , x=x0 ,v=v0,代入运动学方程有: x0 = Acos ,v0 = −Asin . 因此: 2 0 2 0 ( ) v A = x + , arctan( ) 0 0 x v = − . 讨论:(1)相位的物理意义和现代物理学中地位; (2)运动学方程指数表示. 【例 1】一轻弹簧的倔强系数为 k,其下悬有一质量为 m 的盘子,现有一质量为 M 的物体 从离盘 h 高度外自由下落到盘中并和盘子粘在一起,于是盘子开始振动. (1)此时的振动周期与空盘子振动时的周期有何不同? (2)此时的振动振幅多大? (3)取平衡位置为原点,位移以向下为正,并以弹簧开始振动时作为计时起点,求初相, 并写出物体与盘子的振动方程. 【分析】(1)M 落到 m 之前,做自由落体运动,与 m 作完全非弹性碰撞前的最大速度为

=2g动:(2)M与m之间的碰撞是完全非弹性碰撞,因此碰后的速度为,=牛mgh,一 即为开始计时的初速度:(3)由于M落到盘中后,新的平衡位置下移了△x-修,以新的平 衡位置为坐标原点,向下向正方向,所以,=-竖,可解得振动方程 ,神4-受学票,。 k ,r%振动(2)比振动(1)超前或振动(1)比振动(2)落后 ,<%振动(1)比振动(2)超前或振动(2)比振动(1)落后: %=?称这两个振动为同相或同步: 马-g=元称这两个振动为反相。 4.3、简谐振动的能量 动能6=m密=m0 Psn(+-p),势能E==k.fco(ew+pl,又k=mo,所 以,(+5,=,弹簧振子作简谐运动的总能量与振幅的二次方成正比,由于在简谐振动中
5 v = 2gh ;(2)M 与 m 之间的碰撞是完全非弹性碰撞,因此碰后的速度为 gh M m M v0 2 + = , 即为开始计时的初速度;(3)由于 M 落到盘中后,新的平衡位置下移了 k Mg x = ,以新的平 衡位置为坐标原点,向下向正方向,所以, k Mg x0 = − ,可解得振动方程 x = Acos(t +) ,式中 ) 2 ( M m Mh k Mg k Mg A + = + , M m k + = , M m g kh ( ) 2 tan 1 + = − , 2 3 . 4.2.3 简谐振动的旋转矢量图示法 (一)、旋转矢量 简谐振动的方程 x = Acos( t +) ,根据几何学原理可以把 它看作一旋转着的矢 A 在 x 轴上的投影。振幅矢量转动一周, 相当于振动一个周期。 【例 2】 一物体沿 x 轴作简谐振动,振幅为 A,其表达式 用余弦函数表示。若 t=0 时,物体的运动状态分别为 (1) x0 = −A ;(2)过平衡位置向 x 轴正方向运动;(3) 过 x0 = A/ 2 处向 x 轴负方向运动; 图 18-3 (4)过 x0 = A/ 2 处向 x 轴正方向运动;试用矢量图示法确定相应的初相。 (二)、相位差 在比较两个或两个以上的简谐振动时,相位的概念很重要。 例如两个振动: cos( ) 1 = 1 +1 x A t , cos( ) 2 = 2 +2 x A t 相位差 2 1 2 1 = ( t + ) − ( t + ) = − 在同频率的情况下,两个振动的周相差就是它们的初相差。 2 1 振动(2)比振动(1)超前或振动(1)比振动(2)落后; 2 1 振动(1)比振动(2)超前或振动(2)比振动(1)落后; 2 = 1 称这两个振动为同相或同步; 2 −1 = 称这两个振动为反相。 4.3、 简谐振动的能量 动能 sin ( ) 2 1 ) d d ( 2 1 2 2 2 2 = = m A t + t x Ek m ,势能 cos ( ) 2 1 2 1 2 2 2 Ep = k x = k A t + ,又 2 k = m ,所 以, 2 2 1 Ek + Ep = kA ,弹簧振子作简谐运动的总能量与振幅的二次方成正比.由于在简谐振动中, x x0 O x A M(t) t v
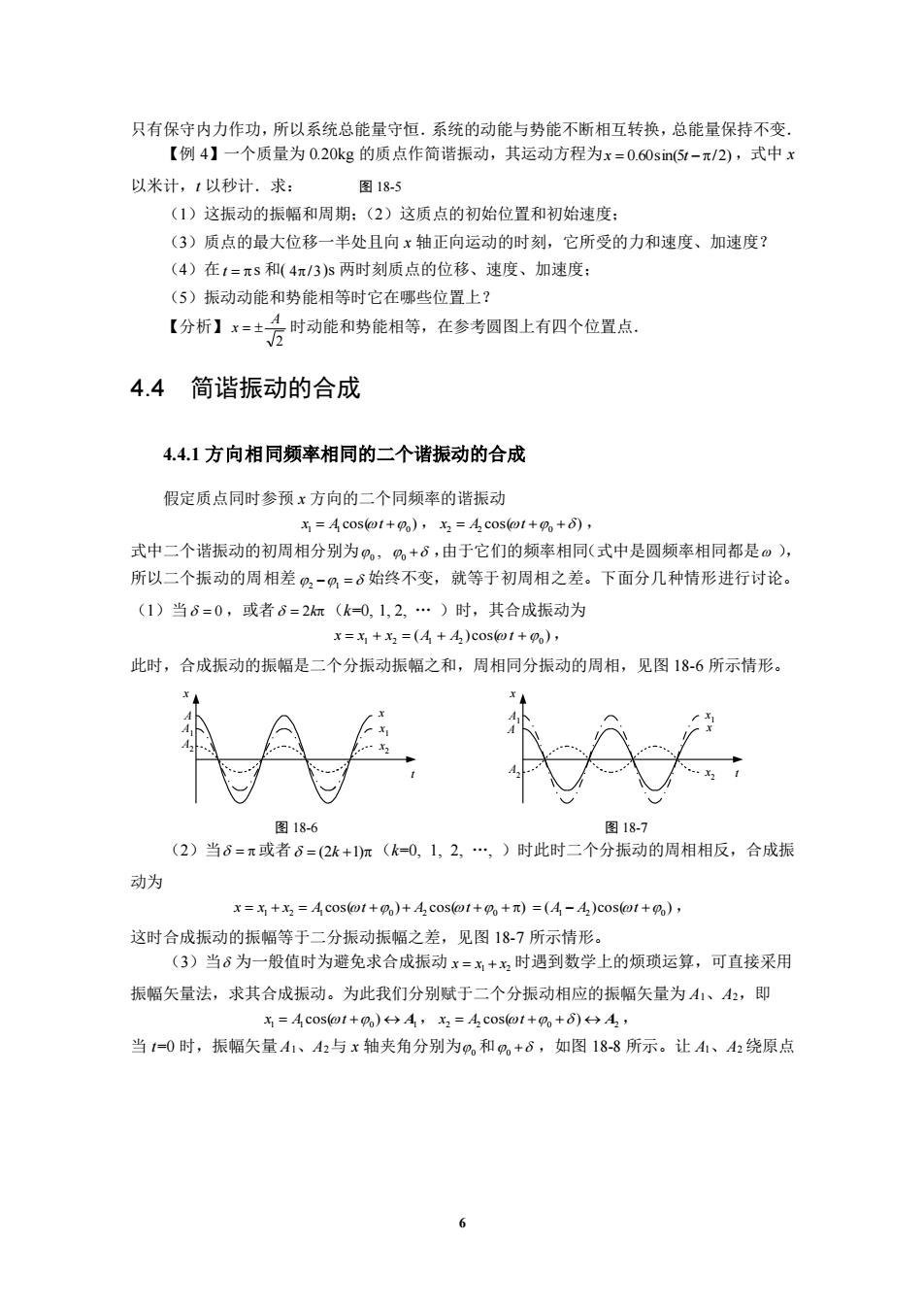
只有保守内力作功,所以系统总能量守恒。系统的动能与势能不断相互转换,总能量保持不变。 【例4】一个质量为020kg的质点作简谐振动,其运动方程为x=0.60sm51-π/2),式中x 以米计,1以秒计.求: 图185 (1)这振动的振幅和周期:(2)这质点的初始位置和初始速度: (3)质点的最大位移一半处且向x轴正向运动的时刻,它所受的力和速度、加速度? (4)在三s和(4/3)s两时刻质点的位移、速度、加速度: (5)振动动能和势能相等时它在哪些位置上? 【分析】±方时动能和势能相等,在参考圆图上有四个位置点, 4.4简谐振动的合成 4.4.1方向相同频率相同的二个谐振动的合成 假定质点同时参预x方向的二个同频率的谐振动 x =Acosot+o),x.A.costot+o+) 式中二个谐振动的初周相分别为,%+6,由于它们的频率相同(式中是圆频率相同都是。) 所以二个振动的周相差%-%=6始终不变,就等于初周相之差。下面分几种情形进行讨论。 (1)当6=0,或者8=2(k=0,1,2,.)时,其合成振动为 x=+=(4+4)0s@1+), 此时,合成振动的振幅是二个分振动振幅之和,周相同分振动的周相,见图18-6所示情形。 图18 (2)当6=π或者6=(2k+1m(k-0,1,2,)时此时二个分振动的周相相反,合成振 动为 x=x+x=A cos(ot+)+A cos(++)=(A-A.)cos(t+) 这时合成振动的振幅等于二分振动振幅之差,见图18-7所示情形 (3)当6为一般值时为避免求合成振动x=,+时遇到数学上的烦琐运算,可直接采用 振幅矢量法,求其合成振动。为此我们分别赋于二个分振动相应的振幅矢量为A1、:,即 x=Acos@t+g)←+A,x=A,cosio1+g+8)←→A, 当1-0时,振幅矢量4、42与x轴夹角分别为0,和%,+6,如图18-8所示。让、2绕原点
6 只有保守内力作功,所以系统总能量守恒.系统的动能与势能不断相互转换,总能量保持不变. 【例 4】一个质量为 0.20kg 的质点作简谐振动,其运动方程为 x = 0.60sin(5t −/2) ,式中 x 以米计,t 以秒计.求: 图 18-5 (1)这振动的振幅和周期;(2)这质点的初始位置和初始速度; (3)质点的最大位移一半处且向 x 轴正向运动的时刻,它所受的力和速度、加速度? (4)在 t = s 和( 4/3 )s 两时刻质点的位移、速度、加速度; (5)振动动能和势能相等时它在哪些位置上? 【分析】 2 A x = 时动能和势能相等,在参考圆图上有四个位置点. 4.4 简谐振动的合成 4.4.1 方向相同频率相同的二个谐振动的合成 假定质点同时参预 x 方向的二个同频率的谐振动 cos( ) 1 = 1 +0 x A t , cos( ) x2 = A2 t +0 + , 式中二个谐振动的初周相分别为 0 , 0 + ,由于它们的频率相同(式中是圆频率相同都是 ), 所以二个振动的周相差 2 −1 = 始终不变,就等于初周相之差。下面分几种情形进行讨论。 (1)当 = 0 ,或者 = 2k (k=0, 1, 2, . )时,其合成振动为 ( ) cos( ) = 1 + 2 = 1 + 2 + 0 x x x A A t , 此时,合成振动的振幅是二个分振动振幅之和,周相同分振动的周相,见图 18-6 所示情形。 x t x x 1 x 2 A A1 A2 x t x x 1 x 2 A1 A A2 图 18-6 图 18-7 (2)当 = 或者 = (2k +1) (k=0, 1, 2, ., )时此时二个分振动的周相相反,合成振 动为 cos( ) cos( ) x = x1 + x2 = A1 t +0 + A2 t +0 + ( )cos( ) = 1 − 2 +0 A A t , 这时合成振动的振幅等于二分振动振幅之差,见图 18-7 所示情形。 (3)当 为一般值时为避免求合成振动 1 2 x = x + x 时遇到数学上的烦琐运算,可直接采用 振幅矢量法,求其合成振动。为此我们分别赋于二个分振动相应的振幅矢量为 A1、A2,即 1 1 0 1 x = A cos(t + ) A , 2 2 0 2 x = A cos(t + + ) A , 当 t=0 时,振幅矢量 A1、A2与 x 轴夹角分别为 0 和 0 + ,如图 18-8 所示。让 A1、A2 绕原点

O以匀角速。逆时针转动时,它们在x轴上的投影分别为n和2,其合成振动x=x+x相应 于振幅矢量A=4+4,且A在A小和A2所构成的平行四边形的对角线位置上,由于该平行四 边形在转动过程中其形状不变,所以其对角线的量值A也不变,而且A绕原点O逆时针 方向转动的角速度也为),即合成振动为同一频率的谐振动。利用=0时的振幅矢量图18-8, 就可求出合振动的振幅矢量A的量值以及它与x轴的夹角m,为此利用关系 A=A+A=A coso+cos(+),A=A,+h,=Asingo+sin(o+), 得到 0) 图18-8 图189 A=居+居=√K+店+244c0s6 晚=子-4边,4=子-4aa】 或者 tand= 4sin网+Asin(%+8 4cosg+4cos偏,+d) 于是合振动初位相为 =arctan sing+sin() 4c050+4C0s%+0)】 求得了A和血,也就求得了1一0时的合成振动的振幅矢量A,于是振幅矢量A绕原点逆时针方 向转动(角速度为圆频率。)时,它在x轴上的投影值x,就给出了该瞬时1的合成振动,即 x=x+x.=Acos+) 式中A,分别为振幅和初位相,并分别由(189)(1810)式给出。 特例(a)当8=2k(k-0,1,2,.)时 A=A+A,功= 于是合振动 x=+=(A+4)c05@1+). 此即前面讨论的情形(1)合成振幅最大,振动最强。 (b)当6=(2k+1)π(k=0,1,2,·)时 A4-4,=0 于是合振动
7 O 以匀角速 逆时针转动时,它们在 x 轴上的投影分别为 x1 和 x2,其合成振动 1 2 x = x + x 相应 于振幅矢量 A = A1 + A2 ,且 A 在 A1 和 A2 所构成的平行四边形的对角线位置上,由于该平行四 边形在转动过程中其形状不变,所以其对角线的量值|A|也不变,而且 A 绕原点 O 逆时针 方向转动的角速度也为 ,即合成振动为同一频率的谐振动。利用 t=0 时的振幅矢量图 18-8, 就可求出合振动的振幅矢量 A 的量值以及它与 x 轴的夹角 0 . 为此利用关系 cos cos( ) Ax = A1x + A2x = A1 0 + A2 0 + , sin sin( ) Ay = A1y + A2 y = A1 0 + A2 0 + , 得到 0 0 + 0 cos( ) A1 cos0 A2 0 + y A A1 A2 O x 2 +0 t y A2 x A1 (t=0 ) A2 (t) A1 (t) 1 +0 t 0 O 图 18-8 图 18-9 2 1 2 cos 2 2 2 1 2 2 A = Ax + Ay = A + A + A A , A A A A Ax cos cos( ) cos 1 0 2 0 0 + + = = , A A A A Ay sin sin( ) sin 1 0 2 0 0 + + = = , 或者 cos cos( ) sin sin( ) tan 1 0 2 0 1 0 2 0 0 + + + + = A A A A , 于是合振动初位相为 cos cos( ) sin sin( ) arctan 1 0 2 0 1 0 2 0 0 + + + + = A A A A . 求得了 A 和 0 也就求得了 t=0 时的合成振动的振幅矢量 A,于是振幅矢量 A 绕原点逆时针方 向转动(角速度为圆频率 )时,它在 x 轴上的投影值 x,就给出了该瞬时 t 的合成振动,即 cos( ) = 1 + 2 = +0 x x x A t , 式中 A, 0 分别为振幅和初位相,并分别由(18-9)(18-10)式给出。 特例(a)当 = 2k (k=0, 1, 2, . )时 A = A1 + A2 , 0 = 0 , 于是合振动 ( )cos( ) = 1 + 2 = 1 + 2 +0 x x x A A t . 此即前面讨论的情形(1)合成振幅最大,振动最强。 (b)当 = (2k +1) (k=0, 1, 2, . )时 | | A = A1 − A2 , 0 = , 于是合振动
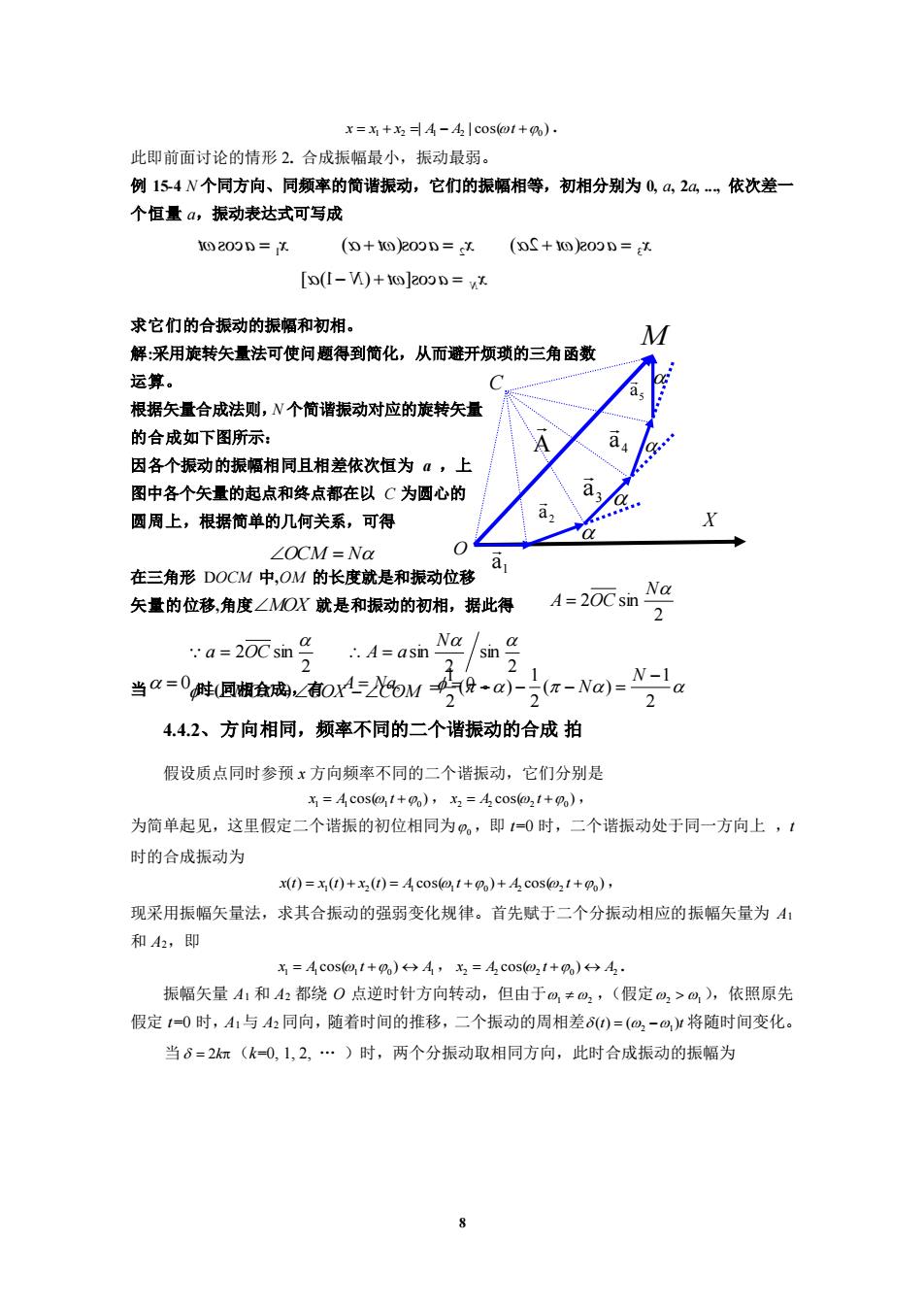
x=+4-c0s1+%): 此即前面讨论的情形2.合成振幅最小,振动最弱。 例154N个同方向、同颜率的简谐振动,它们的振幅相等,初相分别为0,a,2a,依次差一 个恒量a,振动表达式可写成 0200D=X (0+0)200n=x(oS+003n=x [D(1-M)+@]20n=wx 求它们的合振动的振幅和初相。 M 解:采用旋转矢量法可使问题得到简化,从而避开烦琐的三角函数 坛算。 根据矢量合成法则,N个简谐振动对应的旋转矢量 的合成如下图所示: A 因各个振动的振幅相同且相差依次恒为a,上 图中各个矢量的起点和终点都在以C为圆心的 圆周上,根据简单的几何关系,可得 ∠OCM=Na 在三角形DOCM中,0OM的长度就是和振动位移司, 矢量的位移,角度∠MOX就是和振动的初相,据此得 A=20Csin Na :a=2元mgA=asn/sm 2 当a=0阵(圆撰盒魂0r52bM受-a-之(a-Na)-Na 2 4.42、方向相同,频率不同的二个谐振动的合成拍 假设质点同时参预x方向频率不同的二个谐振动,它们分别是 x=AC0s1+0),x2=4c0s21+0), 为简单起见,这里假定二个谐振的初位相同为风,即0时,二个谐振动处于同一方向上,【 时的合成振动为 M)=x)+x2()=4C0s41+P%)+4C0s31+go), 现采用振幅矢量法,求其合振动的强弱变化规律。首先赋于二个分振动相应的振幅矢量为A: 和A2,即 x=4 coso1+0)←A,x,=AC0s@,1+2←→A,. 振幅矢量A1和A都绕O点逆时针方向转动,但由于似≠仙,(假定仙,>),依照原先 假定1一0时,A1与A2同向,随者时间的推移,二个振动的周相差)=(a,-将随时间变化。 当6=2(k-0,1,2,.)时,两个分振动取相同方向,此时合成振动的振幅为
8 O X 1 a 2 a 3 a 4 a 5 a C A M | | cos( ) = 1 + 2 = 1 − 2 +0 x x x A A t . 此即前面讨论的情形 2. 合成振幅最小,振动最弱。 例 15-4 N 个同方向、同频率的简谐振动,它们的振幅相等,初相分别为 0, a, 2a, ., 依次差一 个恒量 a,振动表达式可写成 求它们的合振动的振幅和初相。 解:采用旋转矢量法可使问题得到简化,从而避开烦琐的三角函数 运算。 根据矢量合成法则,N 个简谐振动对应的旋转矢量 的合成如下图所示: 因各个振动的振幅相同且相差依次恒为 a ,上 图中各个矢量的起点和终点都在以 C 为圆心的 圆周上,根据简单的几何关系,可得 在三角形 DOCM 中,OM 的长度就是和振动位移 矢量的位移,角度 就是和振动的初相,据此得 当 时(同相合成),有 4.4.2、方向相同,频率不同的二个谐振动的合成 拍 假设质点同时参预 x 方向频率不同的二个谐振动,它们分别是 cos( ) 1 = 1 1 +0 x A t , cos( ) 2 = 2 2 +0 x A t , 为简单起见,这里假定二个谐振的初位相同为 0 ,即 t=0 时,二个谐振动处于同一方向上 ,t 时的合成振动为 ( ) ( ) ( ) cos( ) cos( ) = 1 + 2 = 1 1 +0 + 2 2 +0 x t x t x t A t A t , 现采用振幅矢量法,求其合振动的强弱变化规律。首先赋于二个分振动相应的振幅矢量为 A1 和 A2,即 1 1 1 0 1 x = A cos( t + ) A , 2 2 2 0 2 x = A cos( t + ) A . 振幅矢量 A1 和 A2 都绕 O 点逆时针方向转动,但由于 1 2 ,(假定 2 1 ),依照原先 假定 t=0 时,A1与 A2 同向,随着时间的推移,二个振动的周相差 (t) ( )t = 2 −1 将随时间变化。 当 = 2k (k=0, 1, 2, . )时,两个分振动取相同方向,此时合成振动的振幅为 t cos a x =1 ) cos( + =2 t a x ) 2 cos( + =3 t a x ] )1− N( +t cos[ a = xN OCM = N MOX 2 2 sin N A = OC 2 2 sin a = OC 2 sin 2 sin N A = a = MOX = COX −COM 2 1 ( ) 2 1 ( ) 2 1 − = − − − = N = 0 A = Na, = 0 。 N

A=月+4,合振动最强 当6=(2k+1)π(k=0,1,2,.)时,分振动取向相反,此时合成振动的振幅为 44-41,合振动最弱。 于是二个频率不同的谐振动合成的结果是:时强时弱,而且这种强弱变化,有其具体的变化规 律。还是假定m,>似,即矢量A比A转得快的情形。 当0时,取A2与A1指向相同,即两矢量重叠,其周相差6=0,这是起始的情形。 当!=4=。时,其周相鉴)=,即北领先山率图,山与私反向,所以合振城 幅A4-4,此时合振动最弱。 当1=么=红时,其周相差64=2,6领先一圈,在与4同向,所以合振动报幅 A=4+4,此时合振动最强。 拍指二个频率不同的谐振动其合成振动的强弱有节奏地变动的现象。一次强弱变化叫一 拍,经历一拍需要时间加 拍频每秒的拍数,它等于=石-不。 【例5】设二个谐振动分别为x0、0,其频率分别为f-8业,上-10业,试求每拍 的时间及拍频。 【解】每拍时间名产万0.拍频=么-62。 2π AM44A44444444444- AAAAAAAAAAAAAAA aa一i 4.4.4、相互垂直的简谐振动的合成 1、方向垂直频率相同的二个谐振动的合成 这里讨论质点同时参预互相垂直的二个谐振动分别在x、y方向, x=4c051+9a),y=4c0s1+风+0). 求其合成振动。事实上质点的合成运动是在x、y平面上,因此人们关心的是质点在y平面上 的运动轨迹以及沿着轨迹怎样运动的问题
9 A = A1 + A2 ,合振动最强 当 = (2k +1) (k=0, 1, 2, . )时,分振动取向相反,此时合成振动的振幅为 | | A = A1 − A2 ,合振动最弱。 于是二个频率不同的谐振动合成的结果是:时强时弱,而且这种强弱变化,有其具体的变化规 律。还是假定 2 1 ,即矢量 A2 比 A1 转得快的情形。 当 t=0 时,取 A2 与 A1 指向相同,即两矢量重叠,其周相差 = ,这是起始的情形。 当 2 1 1 − t = t = 时,其周相差 (t 1 ) = ,即 A2 领先 A1 半圈,A2 与 A1 反向,所以合振动振 幅 | | A = A1 − A2 ,此时合振动最弱。 当 2 1 2 2 − t = t = 时,其周相差 (t 2 ) = 2,A2 领先 A1 一圈,A2与 A1 同向,所以合振动振幅 A = A1 + A2 ,此时合振动最强。 拍. 指二个频率不同的谐振动其合成振动的强弱有节奏地变动的现象。一次强弱变化叫一 拍,经历一拍需要时间 2 1 2 − . 拍频.. 每秒的拍数,它等于 2 1 2 1 2 = f − f − . 【例 5】 设二个谐振动分别为 ( ) 1 x t 、 ( ) 2 x t ,其频率分别为 1 f =8Hz, 2 f =10Hz,试求每拍 的时间及拍频。 【解】 每拍时间= 2 1 2 ( ) ( ) 2 2 2 1 2 1 2 1 = − = − = − f f f f s . 拍频 = f 2 − f 1 = 2 . 4.4.4、 相互垂直的简谐振动的合成 1、方向垂直频率相同的二个谐振动的合成 这里讨论质点同时参预互相垂直的二个谐振动分别在 x、y 方向。 cos( ) = 1 +0 x A t , cos( ) y = A2 t +0 + . 求其合成振动。事实上质点的合成运动是在 x、y 平面上,因此人们关心的是质点在 xy 平面上 的运动轨迹以及沿着轨迹怎样运动的问题。 t x1 t x2 t x
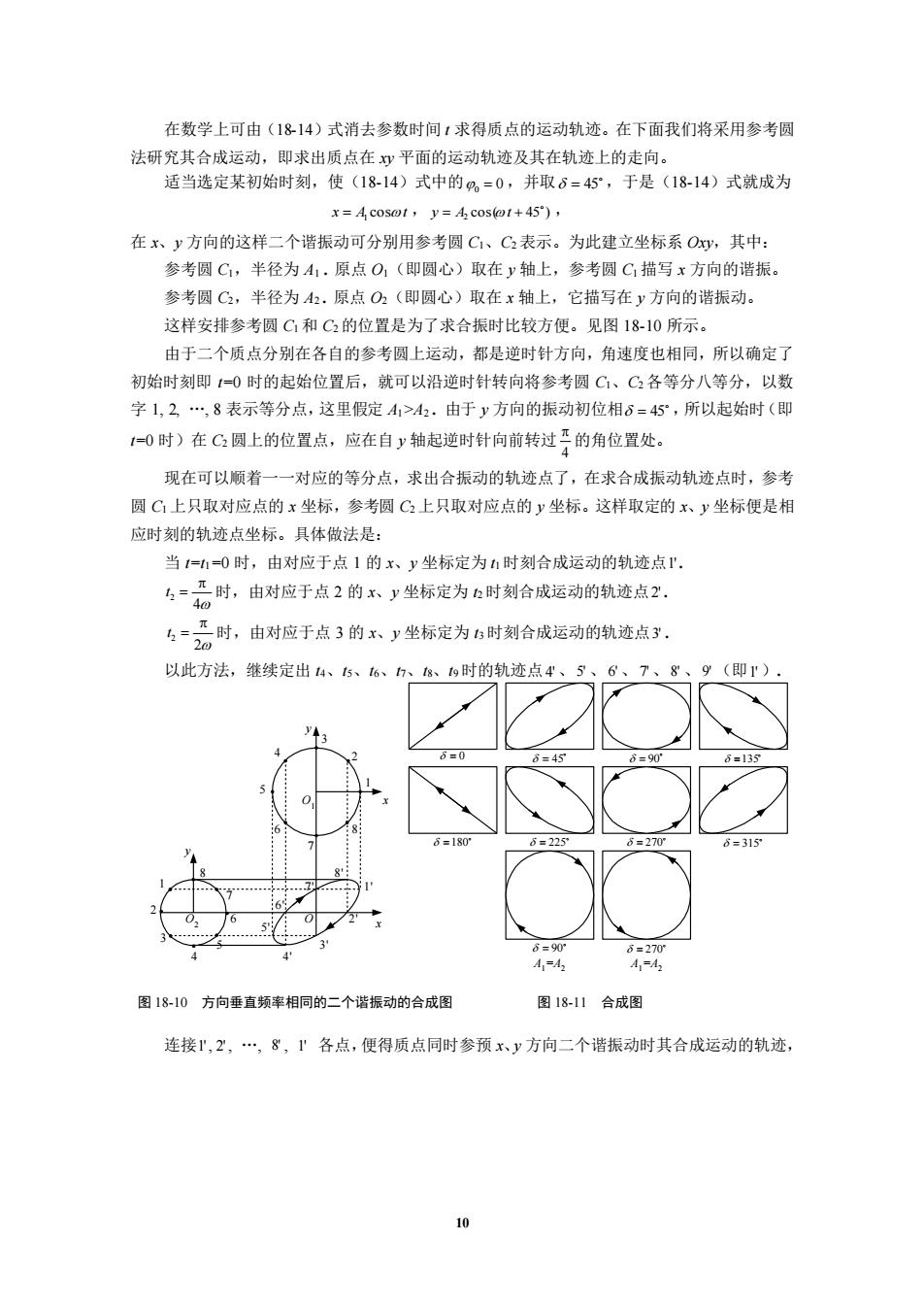
在数学上可由(1814)式消去参数时间1求得质点的运动轨迹。在下面我们将采用参考圆 法研究其合成运动,即求出质点在y平面的运动轨迹及其在轨迹上的走向。 适当选定某初始时刻,使(18-14)式中的%=0,并取6=45,于是(18-14)式就成为 x=Acosot,y=Acos(t+45) 在x、y方向的这样二个谐振动可分别用参考圆C、C2表示。为此建立坐标系O,其中: 参考圆C,半径为A,原点O,(即圆心)取在v轴上,参考圆C描写x方向的诺振 参考圆C2,半径为42.原点O2(即圆心)取在x轴上,它描写在y方向的谐振动。 这样安排参考圆C和CG2的位置是为了求合振时比较方便。见图1810所示。 由于二个质点分别在各自的参考圆上运动,都是逆时针方向,角速度也相同,所以确定了 初始时刻即10时的起始位置后,就可以沿逆时针转向将参考圆C、C各等分八等分,以数 字1,2,.,8表示等分点,这里假定4>4.由于y方向的振动初位相8-45°,所以起始时(即 0时)在C圆上的位置点,应在自y轴起逆时针向前转过工的角位置处。 现在可以顺着一一对应的等分点,求出合振动的轨迹点了,在求合成振动轨迹点时,参考 圆C上只取对应点的x坐标,参考圆C上只取对应点的y坐标。这样取定的x、y坐标便是相 应时刻的轨迹点坐标。具体做法是: 当==0时,由对应于点1的x、y坐标定为时刻合成运动的轨迹点 号时,由对应于点2的、y坐标定为6时刻合成运动的轨迹点之. 4=时,由对应于点3的不y坐标定为时刻合成运动的轨迹点, 以此方法,继续定出4、6、时的轨迹点本、6、7、8g(即r =0 44 图18-10方向垂直频率相同的二个诺振动的合成图 图1811合成图 连接r,工,”,8,”各点,便得质点同时参预x、y方向二个谐振动时其合成运动的轨迹
10 在数学上可由(18-14)式消去参数时间 t 求得质点的运动轨迹。在下面我们将采用参考圆 法研究其合成运动,即求出质点在 xy 平面的运动轨迹及其在轨迹上的走向。 适当选定某初始时刻,使(18-14)式中的 0 = 0 ,并取 = 45 ,于是(18-14)式就成为 x A cost = 1 , cos( 45 ) 2 y = A t + , 在 x、y 方向的这样二个谐振动可分别用参考圆 C1、C2 表示。为此建立坐标系 Oxy,其中: 参考圆 C1,半径为 A1 . 原点 O1(即圆心)取在 y 轴上,参考圆 C1 描写 x 方向的谐振。 参考圆 C2,半径为 A2 . 原点 O2(即圆心)取在 x 轴上,它描写在 y 方向的谐振动。 这样安排参考圆 C1 和 C2 的位置是为了求合振时比较方便。见图 18-10 所示。 由于二个质点分别在各自的参考圆上运动,都是逆时针方向,角速度也相同,所以确定了 初始时刻即 t=0 时的起始位置后,就可以沿逆时针转向将参考圆 C1、C2 各等分八等分,以数 字 1, 2, ., 8 表示等分点,这里假定 A1>A2 . 由于 y 方向的振动初位相 = 45 ,所以起始时(即 t=0 时)在 C2 圆上的位置点,应在自 y 轴起逆时针向前转过 4 的角位置处。 现在可以顺着一一对应的等分点,求出合振动的轨迹点了,在求合成振动轨迹点时,参考 圆 C1 上只取对应点的 x 坐标,参考圆 C2 上只取对应点的 y 坐标。这样取定的 x、y 坐标便是相 应时刻的轨迹点坐标。具体做法是: 当 t=t1=0 时,由对应于点 1 的 x、y 坐标定为 t1 时刻合成运动的轨迹点 1' . 4 2 t = 时,由对应于点 2 的 x、y 坐标定为 t2 时刻合成运动的轨迹点 2' . 2 2 t = 时,由对应于点 3 的 x、y 坐标定为 t3 时刻合成运动的轨迹点 3' . 以此方法,继续定出 t4、t5、t6、t7、t8、t9 时的轨迹点 4'、5' 、6' 、7' 、8' 、9' (即 1' ). 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 x y O1 O2 x 1 ' 2 ' 4 ' 5 ' 6 ' 7 ' 8 ' 3 ' O y = 0 = 45 = 90 =135 =180 = 225 = 270 = 315 = 90 = 270 A1=A2 A1=A2 图 18-10 方向垂直频率相同的二个谐振动的合成图 图 18-11 合成图 连接 1', 2' , ., 8' , 1' 各点,便得质点同时参预 x、y 方向二个谐振动时其合成运动的轨迹