
第七章热力学基础 引言:热学的研究对象和两种研究方法 1.热学是关于温度有关的学问,与我们的日常生活,工农业生产以及各行各业有若密切 关系。 热学是研究热运动的规律对物质宏观性质的影响,以及与物质其他运动形态之间的转化规 律的学科。所谓热运动即组成宏观物体的大量微观粒子的一种永不停息的无规运动。 2.按照研究方法的不同,热学可分为两门学科,即热力学和统计物理学。它们从不同角 度研究热运动,二者相辅相成,彼此联系又互相补充。 3.热力学是研究物质热运动的宏观理论。从基本实验定律出发,通过逻辑推理和数学演 绎,找出物质各种宏观性质的关系,得出宏观过程进行的方向及过程的性质等方面的结论。具 有高度的普适性与可靠性。其缺点是因不涉及物质的微观结构,而将物质视为连续体,故不能 解释物质宏观性质的涨落。 4.统计物理学是研究物质热运动的微观理论。从物质由大量微观粒子组成这一基本事实 出发,运用统计方法,把物质的宏观性质作为大量微观粒子热运动的统计平均结果,找出宏观 量与微观量的关系,进而解释物质的宏观性质。在对物质微观模型进行简化假设后,应用统计 物理可求出具体物质的特性:还可应用到比热力学更为广阔的领域,如解释涨落现象是研究非 线性科学奠基石。第七章气体动理论就是统计物理学的基础。 5.本章为热力学基础主要内容有: 理想气体物态方程: 功、热量: 热力学第一定律: 等温和绝热过程: 7.1内能功和热量准静态过程 一、热力学第零定律 内容:热平衡定律 二、热力学过程 1,热力学过程 当系统的状态随时间变化时,我们就说系统在经历一个热力学过程,简称过程。 推进活塞压缩汽缸内的气体时,气体的体积,密度,温度或压强都将变化,在过程中的任 意时刻,气体各部分的密度,压强,温度都不完全相同 2.非静态过程 显然过程的发生,系统往往由一个平衡状态到平衡受到破坏,再达到一个新的平衡态。从 平衡态破坏到新平衡态建立所需的时间称为弛豫时间,用ī表示。实际发生的过程往往进行的 较快,在新的平衡态达到之前系统又继续了下一步变化。这意味着系统在过程中经历了一系列
第七章 热力学基础 引言:热学的研究对象和两种研究方法 1.热学是关于温度有关的学问,与我们的日常生活,工农业生产以及各行各业有着密切 关系。 热学是研究热运动的规律对物质宏观性质的影响,以及与物质其他运动形态之间的转化规 律的学科。所谓热运动即组成宏观物体的大量微观粒子的一种永不停息的无规运动。 2.按照研究方法的不同,热学可分为两门学科,即热力学和统计物理学。它们从不同角 度研究热运动,二者相辅相成,彼此联系又互相补充。 3.热力学是研究物质热运动的宏观理论。从基本实验定律出发,通过逻辑推理和数学演 绎,找出物质各种宏观性质的关系,得出宏观过程进行的方向及过程的性质等方面的结论。具 有高度的普适性与可靠性。其缺点是因不涉及物质的微观结构,而将物质视为连续体,故不能 解释物质宏观性质的涨落。 4.统计物理学是研究物质热运动的微观理论。从物质由大量微观粒子组成这一基本事实 出发,运用统计方法,把物质的宏观性质作为大量微观粒子热运动的统计平均结果,找出宏观 量与微观量的关系,进而解释物质的宏观性质。在对物质微观模型进行简化假设后,应用统计 物理可求出具体物质的特性;还可应用到比热力学更为广阔的领域,如解释涨落现象是研究非 线性科学奠基石。第七章气体动理论就是统计物理学的基础。 5.本章为热力学基础主要内容有: 理想气体物态方程; 功、热量; 热力学第一定律; 等温和绝热过程; 7.1 内能 功和热量 准静态过程 一、热力学第零定律 内容:热平衡定律 二、热力学过程 1.热力学过程 当系统的状态随时间变化时,我们就说系统在经历一个热力学过程,简称过程。 推进活塞压缩汽缸内的气体时,气体的体积,密度,温度或压强都将变化,在过程中的任 意时刻,气体各部分的密度,压强,温度都不完全相同。 2.非静态过程 显然过程的发生,系统往往由一个平衡状态到平衡受到破坏,再达到一个新的平衡态。从 平衡态破坏到新平衡态建立所需的时间称为弛豫时间,用τ表示。实际发生的过程往往进行的 较快,在新的平衡态达到之前系统又继续了下一步变化。这意味着系统在过程中经历了一系列

非平衡态,这种过程为非静态过程。作为中间态的非平衡态通常不能用状态参量来描述 3.准静态过程 个过程,如果任意时刻的中间态都无限接近于一个平衡态,则此过程为准静态过程。显 然,这种过程只有在进行的“无限缓慢”的条件下才可能实现。对于实际过程则要求系统 状态发生变化的特征时间远远大于弛豫时间【才可近似看作准静态过程。 显然作为准静态过程中间状态的平衡态,其有确定的状态参量值,对于简单系统可用-V 图上的一点来表示这个平衡态。系统的准静态变化过程可用-V图上的一条曲线表示,称之为 过程曲线。准静态过程是一种理想的极限,但作为热力学的基础,我们要首先者重讨论它。 三、功、热量、内能 A、功 1.无摩擦准静态过程 特点是没有摩擦力,外界在准静态过程中对系统的作用力,可以用系统本身的状态参量来 表示。 【例1】如图6-2所示,活塞与汽缸无摩擦,当气体作准静态压缩或膨胀时,外界的压 强P必等于此时气体的压强P,否则系统在有限压差作用下,将失去平衡,称为非静态过程。 若有摩擦力存在,虽然也可使过程进行的“无限缓慢”,但≠P 图62例1图 2.功的表达式 为简化问题,只考虑无摩擦准静态过程的功。当活塞移动微小位移时,系统向外界所 作的元功为 dW=p.·adl=p。·dV 海态过程脚月-P, 系统体积由V1变为V2,系统向外界所作的总功为: w=fp-dv 3.功是过程量 由积分意义可知,用(2)式求出功的大小等于pV图上过程曲线pV)下的面积。比较 a,b下的面积可知,功的数值不仅与初态和末态有关,而且还依赖于所经历的中间状态,功与 过程的路径有关。所以功是过程量。 B、热量(具体物理意义在热力学第一定律中讲述) 2
2 非平衡态,这种过程为非静态过程。作为中间态的非平衡态通常不能用状态参量来描述。 3.准静态过程 一个过程,如果任意时刻的中间态都无限接近于一个平衡态,则此过程为准静态过程。显 然,这种过程只有在进行的 “ 无限缓慢 ” 的条件下才可能实现。对于实际过程则要求系统 状态发生变化的特征时间远远大于弛豫时间τ才可近似看作准静态过程。 显然作为准静态过程中间状态的平衡态,具有确定的状态参量值,对于简单系统可用 p-V 图上的一点来表示这个平衡态。系统的准静态变化过程可用 p-V 图上的一条曲线表示,称之为 过程曲线。准静态过程是一种理想的极限,但作为热力学的基础,我们要首先着重讨论它。 三、功、热量、内能 A、功 1.无摩擦准静态过程 特点是没有摩擦力,外界在准静态过程中对系统的作用力,可以用系统本身的状态参量来 表示。 【例 1】 如图 6-2 所示,活塞与汽缸无摩擦,当气体作准静态压缩或膨胀时,外界的压 强 pe 必等于此时气体的压强 p,否则系统在有限压差作用下,将失去平衡,称为非静态过程。 若有摩擦力存在,虽然也可使过程进行的“无限缓慢”,但 pe p . 图 6-2 例 1 图 2.功的表达式 为简化问题,只考虑无摩擦准静态过程的功。当活塞移动微小位移 dl 时,系统向外界所 作的元功为 dW = pe a dl = pe dV . 在无摩擦准静态过程中 pe = p : dW = p dV . 系统体积由 V1 变为 V2,系统向外界所作的总功为: W p V V V d 2 1 = . 3.功是过程量 由积分意义可知,用(2)式求出功的大小等于 p-V 图上过程曲线 p=p(V)下的面积。比较 a , b 下的面积可知,功的数值不仅与初态和末态有关,而且还依赖于所经历的中间状态,功与 过程的路径有关。所以功是过程量。 B、热量(具体物理意义在热力学第一定律中讲述)

1.热传导 系统和外界存在温差时的能量传递方式。 2.热量 通过热传导过程系统和外界传递的能量。也是一个过程量。 3.热量的单位 和能量单位相同,焦耳,J: C、内能 1.绝热过程中功 如果一个系统经过一个过程,其状态的变化完全是由于机械的或电磁的作用,则称此过程 为绝热过程。在绝热过程中外界对系统所作的功为绝热功。著名的焦耳实验如图6-2所示: 水盛在绝热壁包围的容器中,叶轮所作的机械功和电流所作的电功(I2T)就是绝热功。 焦耳实验结果表明: 用各种不同的绝热过程使物体升高一定的温度,所需的功在实验误差范围内是相等的。 在热力学系统所经过的绝热过程(包括非静态的绝热过程)中,外界对系统所作的功仅取 决于系统的初态和终态。 2.内能 定义内能E:任何一个热力学系统都存在一个称为内能的状态参数,当这个系统由平衡态 1经过任意绝热过程达到另一平衡态2时,系统内能增加等于过程中系统对外界所作的功的负 值,即: E-£=-W (1) 3.热量的定义 若系统由初态1经一非绝热过程达到终态2,在此过程中系统对外界所作的功的负值不再 等于过程前后状态函数内能的变化B,~,我们把二者之差定义为系统在过程中以热量Q的形 式从外界吸取的能量,即: Q=6-6-(-W=6-6+W (2) 在给出热量定义之后我们可以这样定义绝热过程:若系统平衡态的改变只靠机械功或电功 来完成,在系统状态改变的过程中不从外界吸热,也不放热,我们称这种系统为绝热系统,这 种过程为绝热过程。 【注意】 (1)内能为状态函数,热量和功为过程函数。 (2)一定质量的理想气体的内能仅与温度有关,即E=E(T):实际气体的内能也仅仅由状 态参量决定,E=E(V,T). 7.2热力学第一定律
3 1.热传导 系统和外界存在温差时的能量传递方式。 2.热量 通过热传导过程系统和外界传递的能量。也是一个过程量。 3.热量的单位 和能量单位相同,焦耳,J; C、内能 1.绝热过程中功 如果一个系统经过一个过程,其状态的变化完全是由于机械的或电磁的作用,则称此过程 为绝热过程。在绝热过程中外界对系统所作的功为绝热功。著名的焦耳实验如图 6-2 所示: 水盛在绝热壁包围的容器中,叶轮所作的机械功和电流所作的电功(I2RT)就是绝热功。 焦耳实验结果表明: 用各种不同的绝热过程使物体升高一定的温度,所需的功在实验误差范围内是相等的。 在热力学系统所经过的绝热过程(包括非静态的绝热过程)中,外界对系统所作的功仅取 决于系统的初态和终态。 2.内能 定义内能 E:任何一个热力学系统都存在一个称为内能的状态参数,当这个系统由平衡态 1 经过任意绝热过程达到另一平衡态 2 时,系统内能增加等于过程中系统对外界所作的功的负 值,即: E2 − E1 = −W , (1) 3.热量的定义 若系统由初态 1 经一非绝热过程达到终态 2,在此过程中系统对外界所作的功的负值不再 等于过程前后状态函数内能的变化 E2 − E1 ,我们把二者之差定义为系统在过程中以热量 Q 的形 式从外界吸取的能量,即: Q = E2 − E1 − (−W) = E2 − E1 +W , (2) 在给出热量定义之后我们可以这样定义绝热过程:若系统平衡态的改变只靠机械功或电功 来完成,在系统状态改变的过程中不从外界吸热,也不放热,我们称这种系统为绝热系统,这 种过程为绝热过程。 【注意】 (1)内能为状态函数,热量和功为过程函数。 (2)一定质量的理想气体的内能仅与温度有关,即 E=E(T);实际气体的内能也仅仅由状 态参量决定,E=E(V , T). 7.2 热力学第一定律

7.2.1热力学第一定律 1.表述 由《2)式可得:Q=△E+W,这就是热力学第一定律。表述为:系统从外界吸收的热 量,一部分用来使系统的内能增加,一部分用来对外界做功。 2.讨论 (1)本质:能量守恒定律: (2)正负号提定: 系统向外界吸热时2>0,系统向外界放热时Q<0, △E,W的正负号自己思考: (3)微分表达式 对于一个无限小准静态过程,热力学第一定律可以表示为: 0=△E+m (3) (4)对于只有体积功的气体系统,有: Q=AE+∫pdW (4) (5)第一类永动机是不可以造成的 7.2.2第一定律对理想气体等值过程的应用 一、热容和摩尔热容 一个系统温度升高dT时,如果它吸收的热量为dQ,则系统的热容定义为 C=do 比热 c=C Γm. 摩尔热容 C.=M =Mc m 【注意】 因热量与过程有关,故同一系统,在不同过程中的热容量有不同的值,有实际意义的是使 热传递过程在一定条件下进行,因而有常用的定容热量与定压热容量。 二、等体过程等体摩尔热容 1.等体过程及其性质 (1)概念在系统状态变化过程中,气体系统的体积保持不变: (2)特点
4 7.2.1 热力学第一定律 1.表述 由(2)式可得: Q = E +W ,这就是热力学第一定律。表述为:系统从外界吸收的热 量,一部分用来使系统的内能增加,一部分用来对外界做功。 2.讨论 (1)本质:能量守恒定律; (2)正负号规定: 系统向外界吸热时 Q 0 ,系统向外界放热时 Q 0 ; E ,W 的正负号自己思考; (3)微分表达式 对于一个无限小准静态过程,热力学第一定律可以表示为: Q = E + W . (3) (4) 对于只有体积功的气体系统,有: Q E p V V V d 2 1 = + . (4) (5)第一类永动机是不可以造成的。 7.2.2 第一定律对理想气体等值过程的应用 一、热容和摩尔热容 一个系统温度升高 dT 时,如果它吸收的热量为 d Q,则系统的热容定义为 T Q C d d = . 比热 m C c = . 摩尔热容 Mc m MC Cm = = . 【注意】 因热量与过程有关,故同一系统,在不同过程中的热容量有不同的值,有实际意义的是使 热传递过程在一定条件下进行,因而有常用的定容热量与定压热容量。 二、等体过程 等体摩尔热容 1.等体过程及其性质 (1)概念 在系统状态变化过程中,气体系统的体积保持不变; (2)特点

(a)在p-V图上,等体过程为一条平行于p轴的直线: (b)气体对外界作的功为零,由热力学第一定律可知: 无限小等体过程 2,=dE 1) 有限等体过程 Q=△E (2) 2.等体摩尔热容C.m 研究对象:质量为m的理想气体系统,经历一个等体过程,吸热dQV,温升dT,则: 等体摩尔热容 c.出0 由(1)式可得: Cn-4d№=M,s m dT m OT) (3) 实验证明:理想气体的内能仅与温度有关,与体积无关。因此对理想气体有: dE(T.)-M E (4) 由(4)式,质量为m的理想气体在一个等体过程中内能的增量为: -6-6-0-c-0,c“器,S-号 3.几种气体的C一的实验值 三、等压过程等压摩尔热容Cp,m 1.理想气体等压过程及其特点 (I)pV图 (2)无限小过程中系统吸收的热量: 2=d证++gCdr+Nr (5) (3)有限过程系统吸热的热量: O=AE+Ip.dy AE+pAv =CrAT+pAV (6) 2.等压摩尔热容Cp,m (1)定义
5 (a)在 p-V 图上,等体过程为一条平行于 p 轴的直线; (b)气体对外界作的功为零,由热力学第一定律可知: 无限小等体过程 QV = dE . (1) 有限等体过程 Q = E . (2) 2.等体摩尔热容 CV , m 研究对象:质量为 m 的理想气体系统,经历一个等体过程,吸热 dQV ,温升 dT,则: 等体摩尔热容 T Q m M C V v m d d , = , 由(1)式可得: V V v m T E m M T Q m M C ( ) d d , = = . (3) 实验证明:理想气体的内能仅与温度有关,与体积无关。因此对理想气体有: C T m M V V E m M T T E m M dE(T,V) ( )V d ( ) T d = V ,md + = . (4) 由(4)式,质量为 m 的理想气体在一个等体过程中内能的增量为: ( ) 2 1 C , T2 T1 M m E = E − E = Q = V m − , T E m M CV m d , = ,或 T E CV d d = . 3. 几种气体的 CV ,m 的实验值 三、等压过程 等压摩尔热容 Cp, m 1.理想气体等压过程及其特点 (1)p-V 图 (2)无限小过程中系统吸收的热量: C T p V M m Q = dE +W + V ,md + d , (5) (3)有限过程系统吸热的热量: C T p V M m Q E p V E p V V m V V = + = + = + d , 2 1 , (6) 2.等压摩尔热容 Cp, m (1)定义
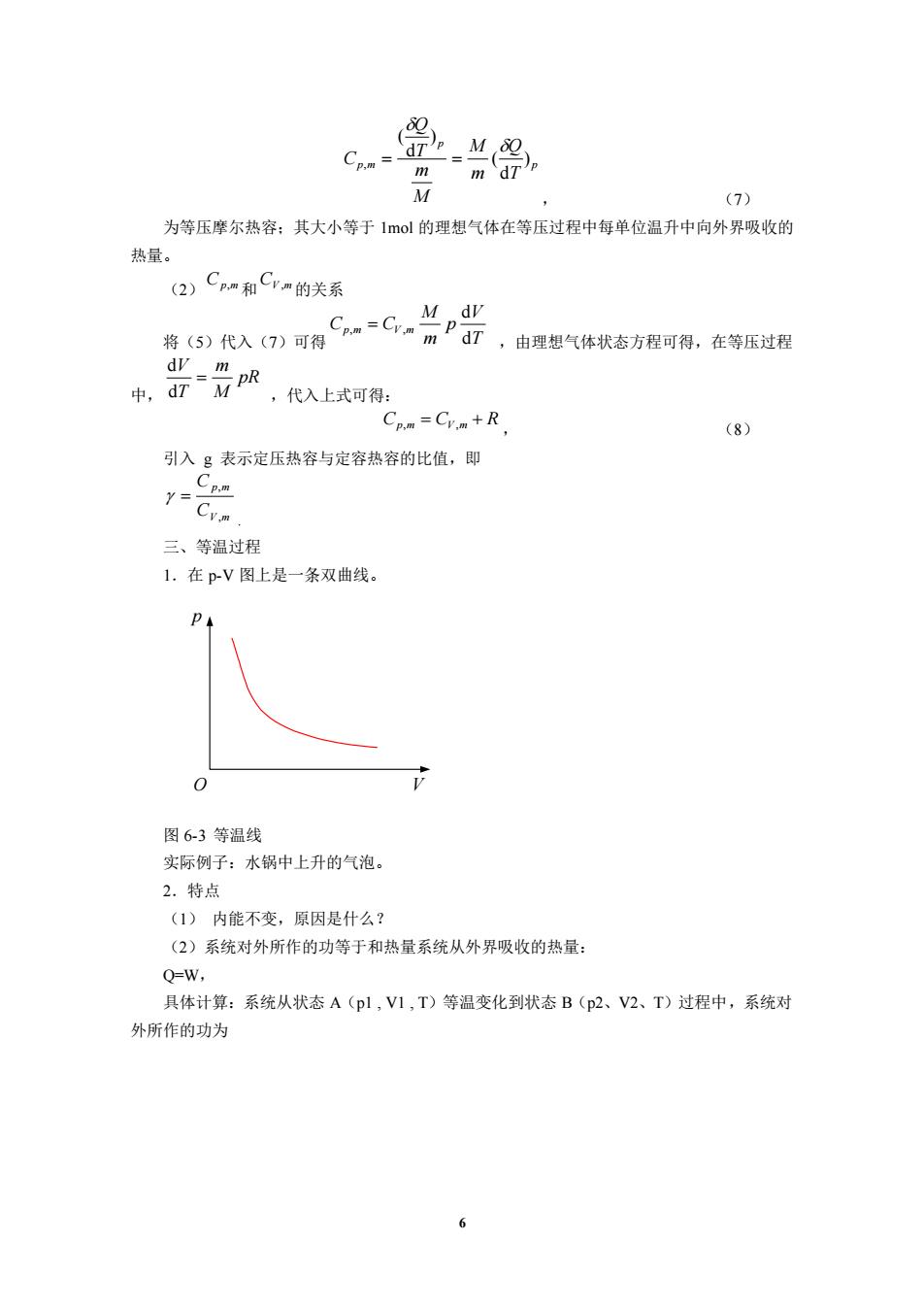
(7) 为等压摩尔热容:其大小等于1ml的理想气体在等压过程中每单位温升中向外界吸收的 热量。 (2)Cpm和Cvm的关系 M dv 将(5)代入(7)可得 mPd7,由理想气体状态方程可得,在等压过程 ,代入上式可得 Cpm Crm+R (8) 引入g表示定压热容与定容热容的比值,即 1-Cvn 三、等温过程 1.在pV图上是一条双曲线。 0 图6-3等温线 实际例子:水锅中上升的气泡。 2.特点 (1)内能不变,原因是什么? (2)系统对外所作的功等于和热量系统从外界吸收的热量: Q=W, 具体计算:系统从状态A(pl,V1,T)等温变化到状态B(p2、V2、T)过程中,系统对 外所作的功为
6 p p p m T Q m M M m T Q C ) d ( ) d ( , = = , (7) 为等压摩尔热容;其大小等于 1mol 的理想气体在等压过程中每单位温升中向外界吸收的 热量。 (2) Cp,m 和 CV ,m 的关系 将(5)代入(7)可得 T V p m M Cp m CV m d d , = , ,由理想气体状态方程可得,在等压过程 中, pR M m T V = d d ,代入上式可得: Cp,m = CV ,m + R , (8) 引入 g 表示定压热容与定容热容的比值,即 V m p m C C , , = . 三、等温过程 1.在 p-V 图上是一条双曲线。 p O V 图 6-3 等温线 实际例子:水锅中上升的气泡。 2.特点 (1) 内能不变,原因是什么? (2)系统对外所作的功等于和热量系统从外界吸收的热量: Q=W, 具体计算:系统从状态 A(p1 , V1 , T)等温变化到状态 B(p2、V2、T)过程中,系统对 外所作的功为
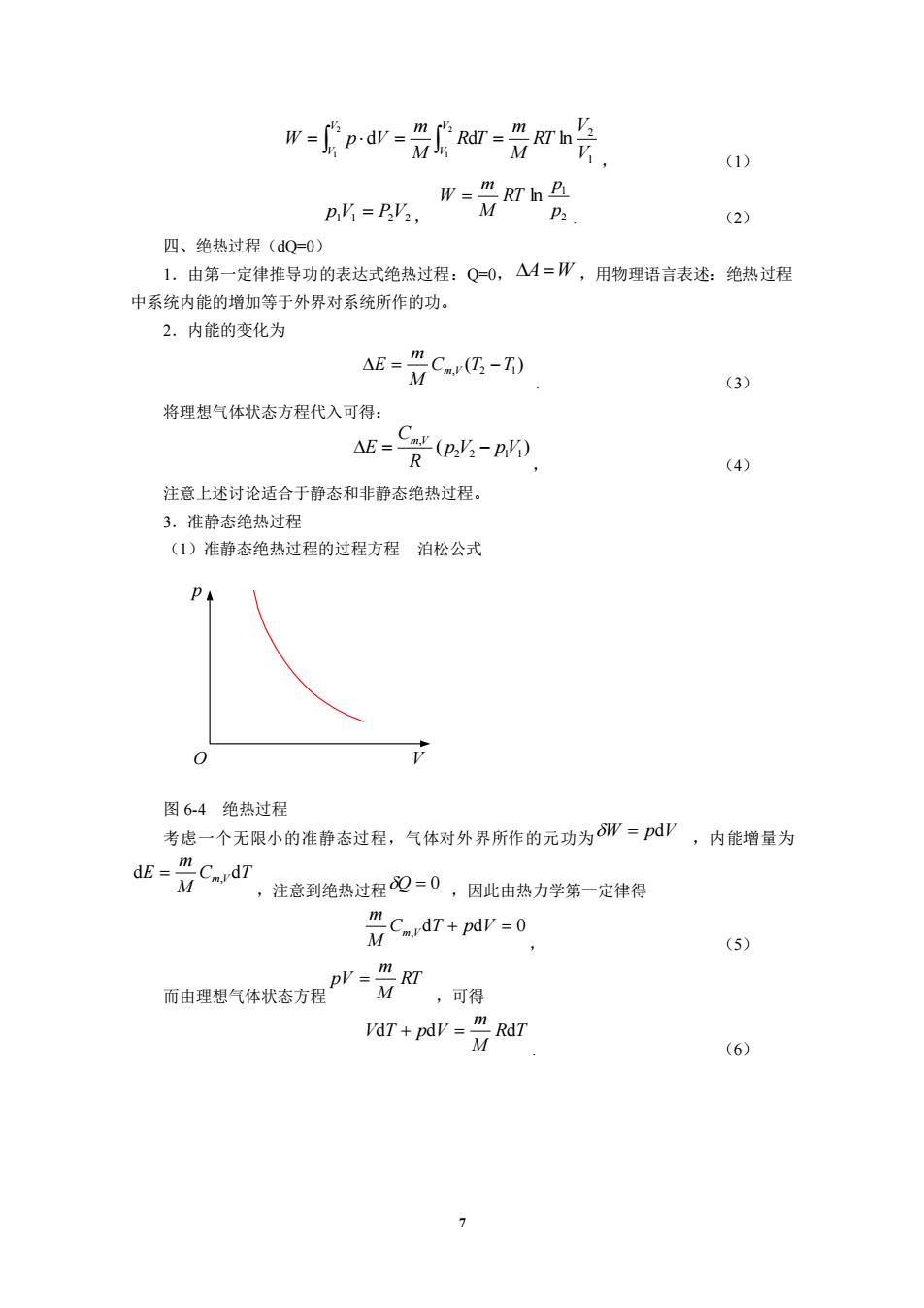
pd Ra M 1) PV=PV,. M (2) 四、绝热过程(dQ-0) 1.由第一定律推导功的表达式绝热过程:Q=0,△4=W,用物理语言表述:绝热过程 中系统内能的增加等于外界对系统所作的功。 2.内能的变化为 AE=MCav(T-T) 3) 将理想气体状态方程代入可得: AE-C(pV:-pY) (4) 注意上述讨论适合于静态和非静态绝热过程 3.准静态绝热过程 (1)准静态绝热过程的过程方程泊松公式 0 图64绝热过程 考虑一个无限小的准静态过程,气体对外界所作的元功为聊=PP,内能增量为 E-Cd ,注意到绝热过程0=0,因此由热力学第一定律得 C dT+-0 (5) 而理想气作态方我P一灯 ,可得 r+pr-是随7 (6)
7 1 2 d d ln 2 1 2 1 V V RT M m R T M m W p V V V V V = = = , (1) p1V1 = P2V2 , 2 1 ln p p RT M m W = . (2) 四、绝热过程(dQ=0) 1.由第一定律推导功的表达式绝热过程:Q=0, A =W ,用物理语言表述:绝热过程 中系统内能的增加等于外界对系统所作的功。 2.内能的变化为 ( ) C , T2 T1 M m E = m V − . (3) 将理想气体状态方程代入可得: ( ) 2 2 1 1 , p V pV R C E m V = − , (4) 注意上述讨论适合于静态和非静态绝热过程。 3.准静态绝热过程 (1)准静态绝热过程的过程方程 泊松公式 p O V 图 6-4 绝热过程 考虑一个无限小的准静态过程,气体对外界所作的元功为 W = pdV ,内能增量为 C T M m dE = m,V d ,注意到绝热过程 Q = 0 ,因此由热力学第一定律得 C , dT + pdV = 0 M m m V , (5) 而由理想气体状态方程 RT M m pV = ,可得 R T M m VdT + pdV = d . (6)

由(5)解出d工,代入(6)式可得 CVdp+Cvpdv=-Rpdl (7) 注意到C=C+R和 C,代入()式可得: P,在可以视 为常数的条件下,两边积分可得 pl?=const (8) 这就是绝热过程的过程方程,也被称为泊松方程。 对于一定的理想气体系统,可 V-iT const (9) 或者 p-T-=const (10) (2)准静态绝热过程功的计算 除了借助第一定律计算功外,对于准静态绝热过程还可利用泊松公式计算如下: 11 此式也可以由上面(4)式直接推出,请自己练习。比较一下: Cny=7-1 4.绝热过程的应用 §9-4焦耳-汤姆逊实验真实气体的内能 大压强空间 多孔塞 小压强空间 气体在绝热条件下,从大压强空间经多孔塞缓慢迁移到小压强空间的过程称为节流过程或 焦耳一汤姆逊过程。 对直实气体。带流膨胀后温度发生变化。 正焦耳一汤姆逊效应:节流膨胀后温度降低: 正焦耳-汤姆逊效应:节流膨胀后温度升高。 对理想气体经历节流过程:
8 由(5)解出 dT,代入(6)式可得: Cm,VVdp +Cm,V pdV = −RpdV , (7) 注意到 Cp,m = CV ,m + R 和 V m p m C C , , = ,代入(7)式可得: p p V dV d = − ,在 可以视 为常数的条件下,两边积分可得 = const pV , (8) 这就是绝热过程的过程方程,也被称为泊松方程。 对于一定的理想气体系统,可得 const 1 = − V T , (9) 或者 const 1 = − − p T . (10) (2)准静态绝热过程功的计算 除了借助第一定律计算功外,对于准静态绝热过程还可利用泊松公式计算如下: 1 [( ) 1] 1 ] 1 1 [ 1 d 1 2 2 1 1 2 1 1 1 1 1 1 2 1 1 1 1 2 1 − − − = − − = − = = − − − p V pV V pV V V V pV V V pV W V V , 此式也可以由上面(4)式直接推出,请自己练习。比较一下: 1 , − = R C m V . 4.绝热过程的应用 §9-4 焦耳-汤姆逊实验 真实气体的内能 气体在绝热条件下,从大压强空间经多孔塞缓慢迁移到小压强空间的过程称为节流过程或 焦耳-汤姆逊过程。 对真实气体,节流膨胀后温度发生变化。 正焦耳-汤姆逊效应:节流膨胀后温度降低; 正焦耳-汤姆逊效应:节流膨胀后温度升高。 对理想气体经历节流过程: 大压强空间 多孔塞 小压强空间

设活塞A移动的距离为xL,活塞B移动的距离为x2,则外力F对气体作功为F1x:气体 对外作功F2x2:则外力对1mol气体做的净功为 △A=Fx1-F2 F=P S:F=pS A4=PK-BV =AE AE-C(G-)=-BV (C+R(T2-T)=0 L=T 这说明理想气体经历节流过程后温度不变。 真实气体经历节流过程后温度变化说明分子间存在相互作用的势能。 实验的应用:干冰的制作。使高压二氧化碳从阀口的小孔喷射出来,从而使温度降低,制 成干冰 7.5循环过程卡诺循环 一、循环过程 1.概念 历史上,热力学理论最初是在研究热机工作过程的基础上发展起来的。在热机中被用来吸 收热量并对外作功的物质叫工质。工质往往经历者循环过程,即经历一系列变化又回到初始状 态。 2.图示 0 图6-5循环过程 若循环的每一阶段都是准静态过程,则此循环可用pV图上的一条闭合曲线表示。箭头表 示过程进行的方向。 3.一般特点 工质在整个循环过程中对外作的净功等于曲线所包围的面积。 二、正循环和逆循环 1。沿顺时针方向进行的循环称为正循环或热循环。 2.正循环的特征 一定质量的工质在一次循环过程中要从高温热源吸热Q1,对外作净功W,又向低温热源
9 设活塞 A 移动的距离为 x1,活塞 B 移动的距离为 x2,则外力 F1 对气体作功为 F1x1;气体 对外作功 F2x2;则外力对 1mol 气体做的净功为 A = F1 x1 − F2 x2 F1 = p1S;F2 = p2S 这说明理想气体经历节流过程后温度不变。 真实气体经历节流过程后温度变化说明分子间存在相互作用的势能。 实验的应用:干冰的制作。使高压二氧化碳从阀口的小孔喷射出来,从而使温度降低,制 成干冰。 7.5 循环过程 卡诺循环 一、循环过程 1.概念 历史上,热力学理论最初是在研究热机工作过程的基础上发展起来的。在热机中被用来吸 收热量并对外作功的物质叫工质。工质往往经历着循环过程,即经历一系列变化又回到初始状 态。 2.图示 1 2 p O V 图 6-5 循环过程 若循环的每一阶段都是准静态过程,则此循环可用 p-V 图上的一条闭合曲线表示。箭头表 示过程进行的方向。 3.一般特点 工质在整个循环过程中对外作的净功等于曲线所包围的面积。 二、正循环和逆循环 1.沿顺时针方向进行的循环称为正循环或热循环。 2.正循环的特征 一定质量的工质在一次循环过程中要从高温热源吸热 Q1,对外作净功 W,又向低温热源 A= P1V1 −P2V2 = E 2 1 1 1 2 2 E =CV (T −T ) = PV − PV ( )( ) 0 T2 =T1 CV + R T2 −T1 =
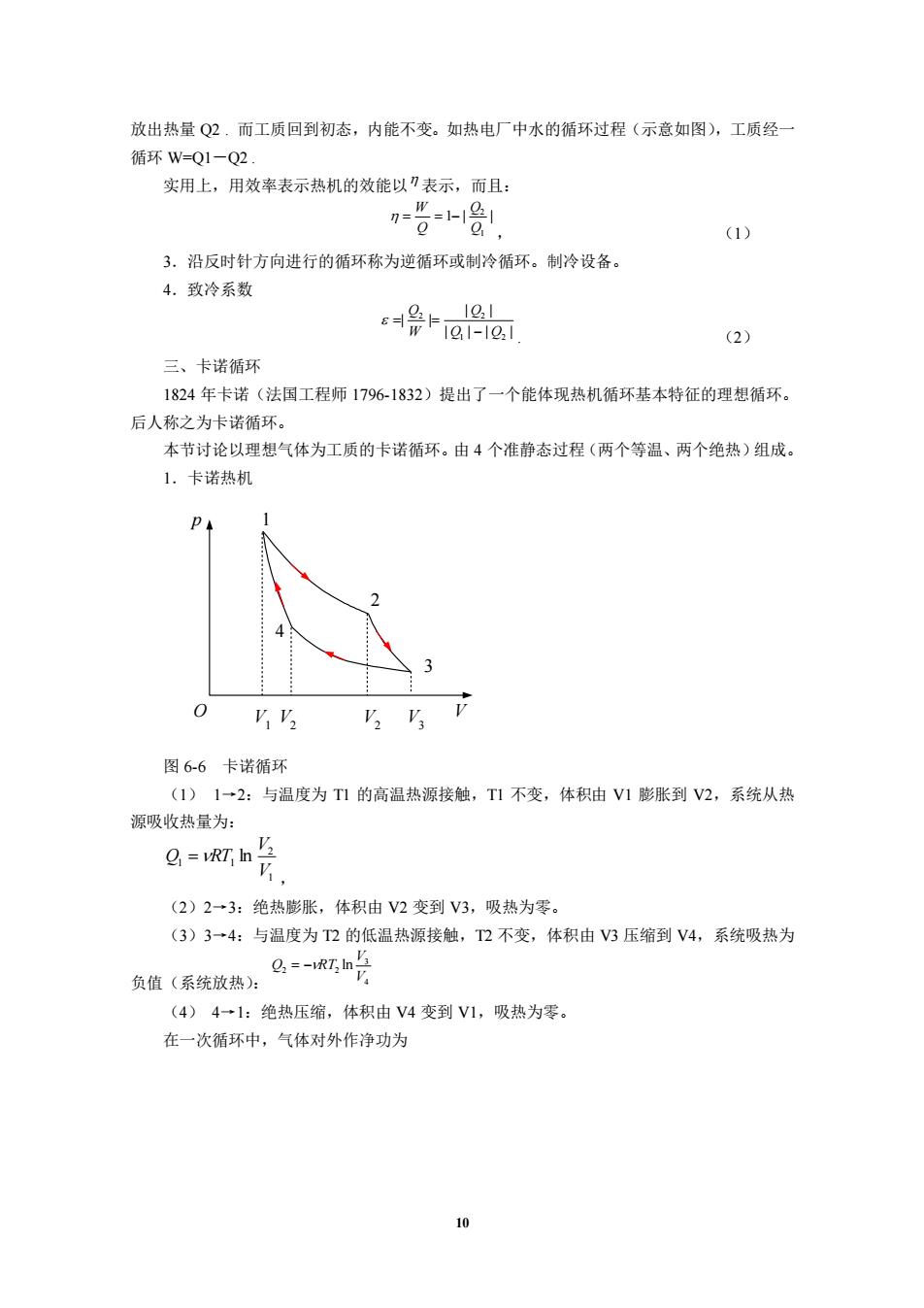
放出热量Q2.而工质回到初态,内能不变。如热电厂中水的循环过程(示意如图),工质经 循环w=Q1-Q2. 实用上,用效率表示热机的效能以表示,而且: (1) 3.沿反时针方向进行的循环称为逆循环或制冷循环。制冷设备。 4.致冷系数 aa1 (2) 三、卡诺循环 1824年卡诺(法国工程师1796-1832)提出了一个能体现热机循环基本特征的理想循环, 后人称之为卡诺循环。 本节讨论以理想气体为工质的卡诺循环。由4个准静态过程(两个等温、两个绝热)组成。 1.卡诺热机 图6-6卡诺循环 (1)1→2:与温度为T1的高温热源接触,T1不变,体积由V1膨胀到V2,系统从热 源吸收热量为: 8=m片 (2)2一3:绝热膨胀,体积由V2变到V3,吸热为零。 (3)3一4:与温度为2的低温热源接触,2不变,体积由V3压缩到V4,系统吸热为 负值(系统放热): 2=-RIn (4)4一1:绝热压缩,体积由V4变到V1,吸热为零。 在一次循环中,气体对外作净功为
10 放出热量 Q2 . 而工质回到初态,内能不变。如热电厂中水的循环过程(示意如图),工质经一 循环 W=Q1-Q2 . 实用上,用效率表示热机的效能以 表示,而且: 1 | | 1 2 Q Q Q W = = − , (1) 3.沿反时针方向进行的循环称为逆循环或制冷循环。制冷设备。 4.致冷系数 | | | | | | | | 1 2 2 2 Q Q Q W Q − = = . (2) 三、卡诺循环 1824 年卡诺(法国工程师 1796-1832)提出了一个能体现热机循环基本特征的理想循环。 后人称之为卡诺循环。 本节讨论以理想气体为工质的卡诺循环。由 4 个准静态过程(两个等温、两个绝热)组成。 1.卡诺热机 p O V 1 2 3 4 V1 V2 V2 V3 图 6-6 卡诺循环 (1) 1→2:与温度为 T1 的高温热源接触,T1 不变,体积由 V1 膨胀到 V2,系统从热 源吸收热量为: 1 2 1 1 ln V V Q =RT , (2)2→3:绝热膨胀,体积由 V2 变到 V3,吸热为零。 (3)3→4:与温度为 T2 的低温热源接触,T2 不变,体积由 V3 压缩到 V4,系统吸热为 负值(系统放热): 4 3 2 2 ln V V Q = −RT (4) 4→1:绝热压缩,体积由 V4 变到 V1,吸热为零。 在一次循环中,气体对外作净功为