
§1.1晶格的周期性 1.品格周期性的描述一一原胞和基矢 品格的共同特点是具有周期性,可以用原胞和基矢来描述。 +原胞:一个品格中最小重复单元(体积最小)如图1.1所示。 +基矢:原胞的边矢量,三维格子的重复单元是平行六面体,ā,b,C是重复单元的边长矢量 +单胞(结晶学元胞):为了反映品格的对称性,常取最小重复单元的几倍作为重复单元 单胞的边在晶轴方向,边长等于该方向上的一个周期,代表单胞三个边的矢量称为单胞的基矢。 +基矢:ā,五,C表示单胞的基矢。在一些情况下,单胞就是原胞,而在一些情况下,单胞不是 例如面心立方品格,如图1.2所示 a-g0+ 4=8(R+) 原跑基东,4=0+刀原的体积=4低×4)-女 单胞基矢:a=ai,五=,c=ak,单胞的体积a=ai,万=,c=ak a Primitive Cell 图1.1 Face-Cemtered( a 图1.2 图1.3 图1.4 2.简单晶格 简单晶格中,某一个原胞只包含一个原子,所有的原子在几何位置和化学性质上是完全等价的。碱
§ 1.1 晶格的周期性 1. 晶格周期性的描述——原胞和基矢 晶格的共同特点是具有周期性,可以用原胞和基矢来描述。 + 原胞:一个晶格中最小重复单元(体积最小)如图 1.1 所示。 + 基矢:原胞的边矢量,三维格子的重复单元是平行六面体, a b c , , 是重复单元的边长矢量 + 单胞(结晶学元胞):为了反映晶格的对称性,常取最小重复单元的几倍作为重复单元。 单胞的边在晶轴方向,边长等于该方向上的一个周期,代表单胞三个边的矢量称为单胞的基矢。 + 基矢: a b c , , 表示单胞的基矢。在一些情况下,单胞就是原胞,而在一些情况下,单胞不是原 胞。 例如面心立方晶格,如图 1.2 所示。 原胞基矢: 1 2 3 ( ) 2 ( ) 2 ( ) 2 a a j k a a k i a a i j = + = + = + 原胞的体积 3 0 1 2 3 1 ( ) 4 v a a a a = = 单胞基矢: a ai b aj c ak = = = , , ,单胞的体积 a ai b aj c ak = = = , , 图 1.1 图 1.2 图 1.3 图 1.4 2. 简单晶格 简单晶格中,某一个原胞只包含一个原子,所有的原子在几何位置和化学性质上是完全等价的。碱

金属具有体心立方品格结构:u、Ag和Cu具有面心立方品格结构,它们均为简单晶格。 简单立方晶格 如图1.3所示,原胞为简单立方晶格的立方单元,基矢a=a,a=,ā=ak 原胞体积:=a:(a,×a,)=心一一原胞中只包含一个原子 面心立方晶格 如图1.3所示,八个顶角上各有一个原子,六个面的中心有6个原子故称面心立方。 由立方体的顶点到三个近邻的面心引三个基失ā,4,可 a=(a/20+k) a2=(a/2(k+i) 花矢8-a20+》限题件期=a低×店)产 原胞中只包含一个原子 体心立方晶格 体心立方:除项角上有原子外,还有一个原子在立方体的中心,故称体心。就整个空间的晶格来看, 完全可把原胞的顶点取在原胞的体心上。这样心就变成角,角也就变成心。如图1.4所示。 由立方体的中心到三个顶点引三个基矢a,ā2,ā a=(a/2(-i+j+k) a2=(a/2i-j+k) 影铁4=020-+南.=4aa)-9展中只色含-个限子 3.复式晶格 复式格子包含两种或两种以上的等价原子。 一种是不同原子或离子构成的品体,如:NaC1、CsCl、Zns等: 一种是相同原子但几何位置不等价的原子构成的晶体,如:具有金刚石结构的C、Si、Ge以及具有 六角密排结构的Be、Mg、Z知等 复式格子的特点:不同等价原子各自构成相同的简单晶格(子晶格),复式格子由它们的子晶格相 套而 +NC1由'和CT结合而成(如图1.5所示。),是一种典型的离子晶体,阳构成一个面心立方 晶格:C汇也构成相同的一个面心立方品格。两个面心立方子品格各自的原胞具有相同的基矢,由它们相 套形成NaCI复式品格 CsC1结构是由两个简立方的子晶格彼此沿立方体空间对角线位移1/2的长度套构而成。如图1.5 所示
金属具有体心立方晶格结构;Au、Ag 和 Cu 具有面心立方晶格结构,它们均为简单晶格。 简单立方晶格 如图 1.3 所示, 原胞为简单立方晶格的立方单元,基矢 1 2 3 a ai a aj a ak = = = , , 原胞体积: 3 0 1 2 3 v a a a a = = ( ) ——原胞中只包含一个原子 面心立方晶格 如图 1.3 所示,八个顶角上各有一个原子,六个面的中心有 6 个原子故称面心立方。 由立方体的顶点到三个近邻的面心引三个基矢 1 2 3 a a a , , 基矢 1 2 3 ( / 2)( ) ( / 2)( ) ( / 2)( ) a a j k a a k i a a i j = + = + = + 原胞体积 3 0 1 2 3 1 ( ) 4 v a a a a = = 原胞中只包含一个原子 体心立方晶格 体心立方:除顶角上有原子外,还有一个原子在立方体的中心,故称体心。就整个空间的晶格来看, 完全可把原胞的顶点取在原胞的体心上。这样心就变成角,角也就变成心。如图 1.4 所示。 由立方体的中心到三个顶点引三个基矢 1 2 3 a a a , , 基矢 1 2 3 ( / 2)( ) ( / 2)( ) ( / 2)( ) a a i j k a a i j k a a i j k = − + + = − + = − + , 3 0 1 2 3 1 ( ) 2 v a a a a = = 原胞中只包含一个原子 3. 复式晶格 复式格子包含两种或两种以上的等价原子。 一种是不同原子或离子构成的晶体,如:NaCl、CsCl、ZnS 等; 一种是相同原子但几何位置不等价的原子构成的晶体,如:具有金刚石结构的 C、Si、Ge 以及具有 六角密排结构的 Be、Mg、Zn 等; 复式格子的特点:不同等价原子各自构成相同的简单晶格(子晶格),复式格子由它们的子晶格相 套而成。 + NaCl 由 Na + 和 Cl -结合而成(如图 1.5 所示。),是一种典型的离子晶体,Na + 构成一个面心立方 晶格;Cl -也构成相同的一个面心立方晶格。两个面心立方子晶格各自的原胞具有相同的基矢,由它们相 套形成 NaCl 复式晶格。 CsCl 结构是由两个简立方的子晶格彼此沿立方体空间对角线位移 1/2 的长度套构而成。如图 1.5 所示
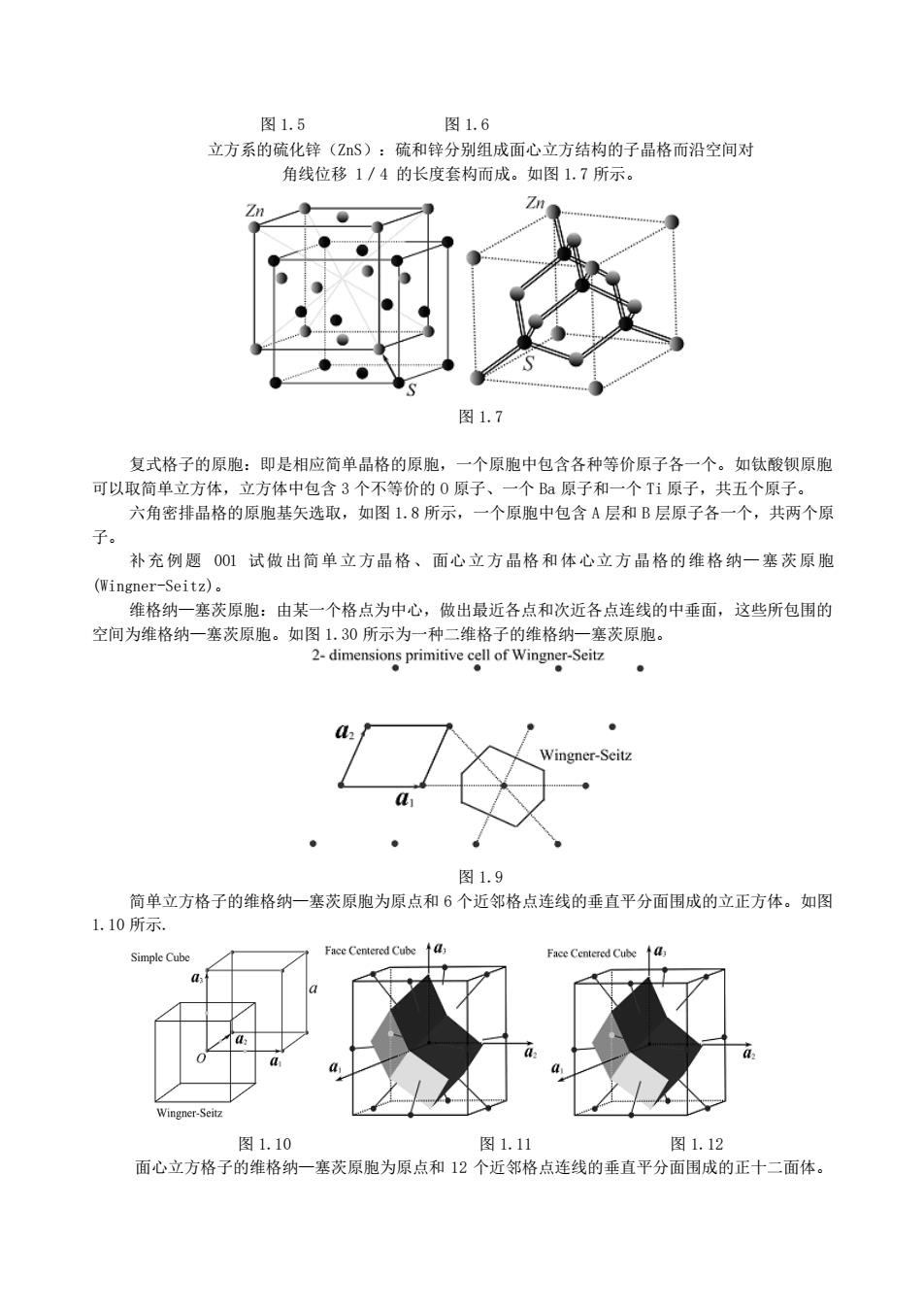
图1.5 图1.6 立方系的硫化锌(ZS):硫和锌分别组成面心立方结构的子品格而沿空间对 角线位移1/4的长度套构而成。如图1.7所示。 图1.7 复式格子的原胞:即是相应简单晶格的原胞,一个原胞中包含各种等价原子各一个。如钛酸钡原胞 可以取简单立方体,立方体中包含3个不等价的0原子、一个B阳原子和一个Ti原子,共五个原子。 六角密排品格的原胞基矢选取,如图1,8所示,一个原胞中包含A层和B层原子各一个,共两个原 子。 补充例题001试做出简单立方品格、面心立方晶格和体心立方晶格的维格纳一塞茨原胞 (Wingner-Seitz). 维格纳一塞茨原胞:由某一个格点为中心,做出最近各点和次近各点连线的中垂面,这些所包围的 空间为维格纳一塞茨原胞。如图1.30所示为一种二维格子的维格纳一塞茨原胞。 2.dimensions primitive cell of Wingner-Seitz Wingner-Scit 图1.9 简单立方格子的维格纳一塞茨原胞为原点和6个近邻格点连线的垂直平分面围成的立正方体。如图 1.10所示 ace Centered Cube↑ 图1.10 图1.11 图1.12 面心立方格子的维格钠一塞茨原胞为原点和12个近邻格点连线的垂直平分面围成的正十二面体
图 1.5 图 1.6 立方系的硫化锌(ZnS):硫和锌分别组成面心立方结构的子晶格而沿空间对 角线位移 1/4 的长度套构而成。如图 1.7 所示。 图 1.7 复式格子的原胞:即是相应简单晶格的原胞,一个原胞中包含各种等价原子各一个。如钛酸钡原胞 可以取简单立方体,立方体中包含 3 个不等价的 O 原子、一个 Ba 原子和一个 Ti 原子,共五个原子。 六角密排晶格的原胞基矢选取,如图 1.8 所示,一个原胞中包含 A 层和 B 层原子各一个,共两个原 子。 补充例题 001 试做出简单立方晶格、面心立方晶格和体心立方晶格的维格纳—塞茨原胞 (Wingner-Seitz)。 维格纳—塞茨原胞:由某一个格点为中心,做出最近各点和次近各点连线的中垂面,这些所包围的 空间为维格纳—塞茨原胞。如图 1.30 所示为一种二维格子的维格纳—塞茨原胞。 图 1.9 简单立方格子的维格纳—塞茨原胞为原点和 6 个近邻格点连线的垂直平分面围成的立正方体。如图 1.10 所示. 图 1.10 图 1.11 图 1.12 面心立方格子的维格纳—塞茨原胞为原点和 12 个近邻格点连线的垂直平分面围成的正十二面体

如图1.11所示体心立方格子的维格纳一塞茨原胞为原点和8个近邻格点连线的垂直平分面围成的正八面 体,和沿立方轴的6个次近邻格点连线的垂直平分面割去八面体的六个角,形成的14面体。八个面是正 六边形,六个面是 正四边形 如图1.12所示。 4。晶格周期性的描述一布拉伐格子 Crystal ● 。* ●。 ●】 ● ● ●● ● ● ● ● ● Basis+Lattice=Crystal 图1.13 图1.13基元是多个原子,二维布拉伐格子是斜方格子时晶体的构成
如图 1.11 所示体心立方格子的维格纳—塞茨原胞为原点和 8 个近邻格点连线的垂直平分面围成的正八面 体,和沿立方轴的 6 个次近邻格点连线的垂直平分面割去八面体的六个角,形成的 14 面体。八个面是正 六边形,六个面是正四边形。如图 1.12 所示. 4. 晶格周期性的描述 — 布拉伐格子 图 1.13 图 1.13 基元是多个原子,二维布拉伐格子是斜方格子时晶体的构成