
第五章声子川.热性质 声子:决定材料的热学性质,通过散射电子,影响导体的电输运性质 声子产生:在晶体中,声子是如何产生或激发的? ·外部干扰-振动或声波传导 ·粒子散射-能量转换成晶格振动 ·热(KT)-在任意有限的温度下(T≠0K激发 热声子 考虑一个处于能级E的系统 占据几率 P(E)exp 在温度T En-3 Boltzmann因子
1 第五章 声子 II. 热性质 声子 :决定材料的热学性质,通过散射电子,影响导体的电输运性质 声子产生 :在晶体中,声子是如何产生或 激发的? • 外部干扰 – 振动或声波传导 • 粒子散射 – 能 量转换成晶格振动 • 热 (KBT) –在任意有限的温度下 (T≠0K) 激发 占据几率 在温度 T “Boltzmann因子” En En-3 En-1 热声子 : 考虑一个处于能级En的系统 ⎟⎟⎠⎞ ⎜⎜⎝⎛−∝ TkE exp)P(E Bn n

模式Ko 激发能级幅度(门)与能量 n+ 2 平均声子数 ∑sPE,) ∑sep ∑PE,) ∑e Es kBT ∑ (s+1/2)n0 s exp kBT (s+1/2)no kBT dx 其中x= no exp (-sx kBT 的Planck分布 1 n(o,T))= 每个处于⊙模,平均激发声子 o exp kgT
2 激发能级幅度 ( n ) 与 能 量 ,k ω ρ 模式 ( ) ( ) ( ) ( ) Tk ω x sxexp sxexp dx d Tk 1/2)(s ω exp Tk 1/2)(s ω exp s Tk E exp Tk E exp s EP EP s n B s s s B s B s B s s B s s s s s η η η = − − − = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = = ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ 其中 平均声子 数 的Planck分布 每个 处于 ω 模,平均激发声子 1 Tk ω exp 1 ω T), n( B −⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = η ω 2 1 n ⎟η ⎠ ⎞ ⎜ ⎝ ⎛ +
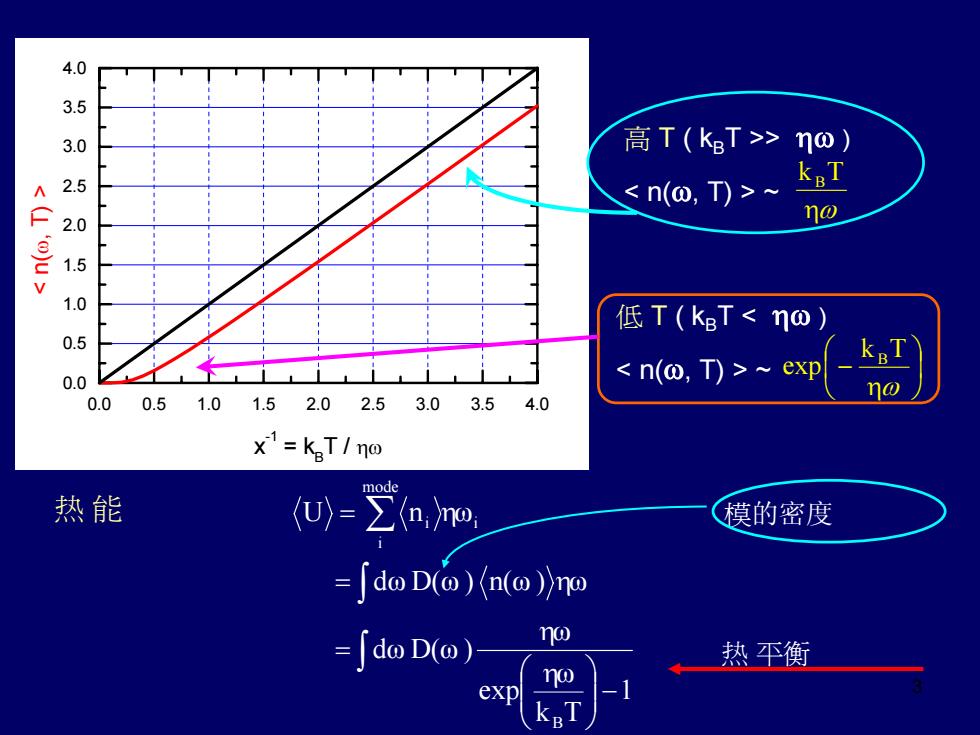
4.0 3.5 3.0 高T(kT>o) kaT A 2.5 ≤n(o,T)> 2.0 no 1.5 1.0 低T(k:T~exp no 0.0 0.51.01.52.02.53.03.54.0 x"=KgT/no 热能 Uy-芝nm 模的密度 =do D(o)(n(o)no =「doD(o) rw 热平衡 ro exp
3 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 x -1 = k BT / ηω 高 T ( k BT >> ηω ) ~ 低 T ( k BT ~ 1 Tk ω exp ω ω d ω ) D( ω d ω ) D( ω ) n( ω nU ω B i mode i i −⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = = = ∫ ∫ ∑ η η η 热 能 η 热 平衡 模的密度 η ω Tk B ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − η ω Tk exp B

态(模)密度:在k-空间中均匀分布 1DD(k三态密度=在k点处单位k的态数目 Dk)dk从k到k+dk的态数目 线型原子链长度为L携带N+1个粒子,粒子间距为a. 边界条件:u)=0和uN()=0 固定点 S=0 S=N us(t)=u exp[-iok.t]sin(ska) 其中k= 元2π3元4πN-1)元 LLLL.1 SN za 为什么没有Nπ/L的k许可值t?us(①csin =sin(sπ)=0 所有的都没有运动. 每间隔 Ak- 。有一个模 fork≤ 单位k区间的模数目 D(k)= a for k>
4 态 (模)密度: 在k-空间中均匀分布 1D D(k)≣态密度 =在k点处单位 k 的态数目 D(k)dk从k 到 k+dk 的态数目 线型原子链长度为 L 携带 N+1 个粒子,粒子间距为 a. 边界条件 : u0(t)=0 和 uN(t)=0 固定点 L π Δk = ⎪⎩ ⎪⎨⎧ > ≤ = a π kfor 0 a π kfor π L D(k) s=0 s=N us(t)=u exp[-iωk,pt] sin(ska) 其中 k= L-(N 1)π . , L4π , L3π , L2π , Lπ 为什么没有 Nπ/L的k许可值? us(t) ∝ =0 所有的都没有运动. 每间隔 单位 k区间的模数目 ( ) π π ssin L asN sin ⎟ =⎠⎞ ⎜⎝⎛ 有一个模

把介质看作无边界的,但要求所得到的解在长距离L上具有周期性.即周期 性边界条件 u(sa)=u(sa+L) 对于一个大的体系而言 us(t)=u exp[i(ska-kpt)] 每间隔 Ak= 2π 有1个模 L 单位k区间的模数目 D(k)= 对于-≤k≤ 2元 a a D(k)dk = dk且有±k2个 =0 其他 2元 D(@)do=2D(k)dk 2D(k)- do 单位频率区间的模数 D(0)=2Dk) dk 2D(k)2D(k) do do/dk 色散关系 奇点在V。=0,由⊙k)决定
5 把介质看作无边界的,但要求所得到的解在长距离L上具有周期性.即周期 性边界条件 u(sa)=u(sa+L) 对于一个大的体系而言 us(t)=u exp[ i(ska-ωk,pt) ] 其中 k= . , L6π , L4π , L2π ,0 ±±± L 2π 每间隔 Δk = 有1个模 其他 对于 0 a π k a π 2π L D(k) = 单位k区间的模数目 = ≤≤− dω dω dk ω D( ω D(k)2D(k)dk2)d 2k dk 2π L D(k)dk = = = 且有 ± 个 vg 2D(k) ω /dkd 2D(k) dω dk D( ω = D(k)2) == 单位频率区间的模数 奇点在 vg=0, 由 ω(k)决定 色散关系
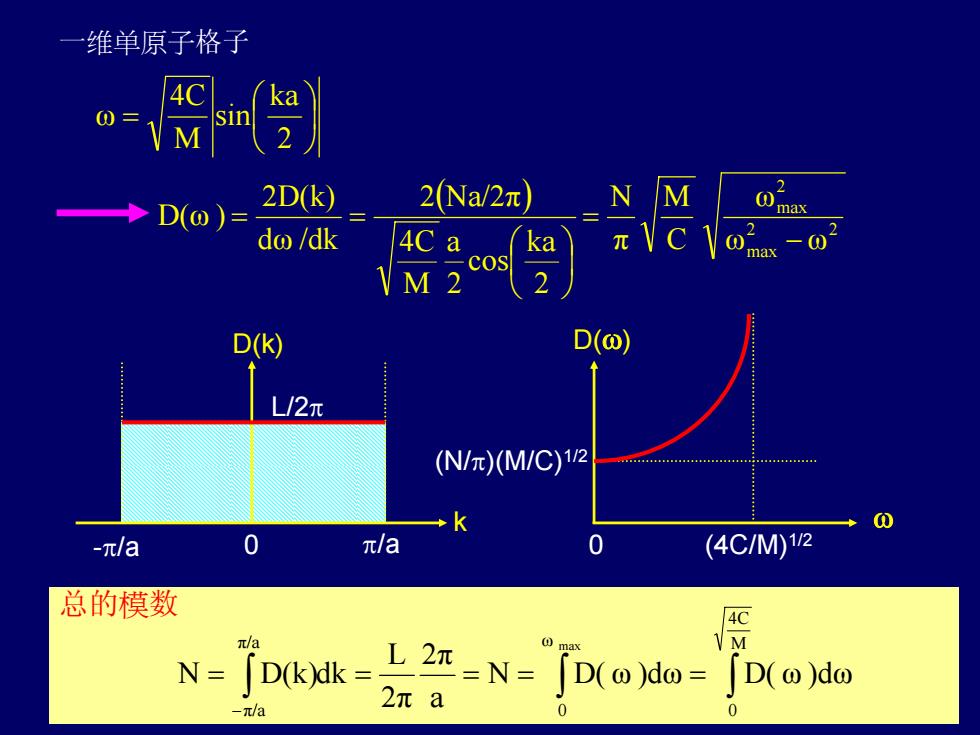
一维单原子格子 ka \M 2 2Na/2元 N M D(o)= 2D(k) max do /dk 4C a a 02 D(k) D(@) LU/2元 (N/m)M/C)12 -π/a 0 π/a 0 (4C/M12 总的模数 VM N=D(kXk=12z-N=[D(o)do=D(o)do π/a max -π/a 2πa 0 0
6 一维单原子格子 ( ) 2 2 max 2 max ωω ω C M π N 2 ka cos 2 a M 4C 2 Na/2π ω /dkd 2D(k) ω ) D( 2 ka sin M 4C ω − = ⎟⎠⎞ ⎜⎝⎛ == ⎟⎠⎞ ⎜⎝⎛ = D(ω) k ω D(k) L/2π -π/a 0 π/a (N/π)(M/C)1/2 (4C/M)1/2 0 总的模数 D(N ω ω D()d ω ω )d a 2π 2π L dkD(k)N M 4C 0 ω 0 π/a π/a max ∫ ∫∫ = === = −

二维情况: 周期性边界条件,在边长为L的正方形中有NP个原胞 exp[i(kx+k y)]exp[i(kx(x+L)+k(y+L)) 当Kx,K,=0,± 4π6元 工一L,-L 在k-空间中单位面积的模数 在k-空间里波矢从k到k+dk的模数 L D(k)dk= △k△k dk,dky= 2πkdk 4π 单位频率区域的模数 D(O)= D(k) A2元k1 do/dk 4 D(k)V 三维情况: D(0)= 4k21 do/dk 8n3
7 二维情况 : 周期性边界条件, 在边长为L 的正方形中有N2个原胞 exp[ i(kxx+kyy) ] = exp[ i( kx(x+L) + ky(y+L) ) ] 当 kx, ky = . , L6π , L4π , L2π ,0 ±±± 在k-空间中单位面积的模数 2 2 2 yx 4π L L 2π Δk Δk 1 ⎟ = ⎠⎞ ⎜⎝⎛ = − 在k-空间 里波矢从k 到 k+dk的模数 π dkk 2 4π L dkdk Δk Δk 1 D(k)dk 22 yx yx = = 单位频率区域的模数 g 2 v 1 π k 2 4π A ω /dkd D(k) D( ω ) == g 2 3 v 1 π k 4 8π V ω /dkd D(k) 三维情况 : D( ω ) ==
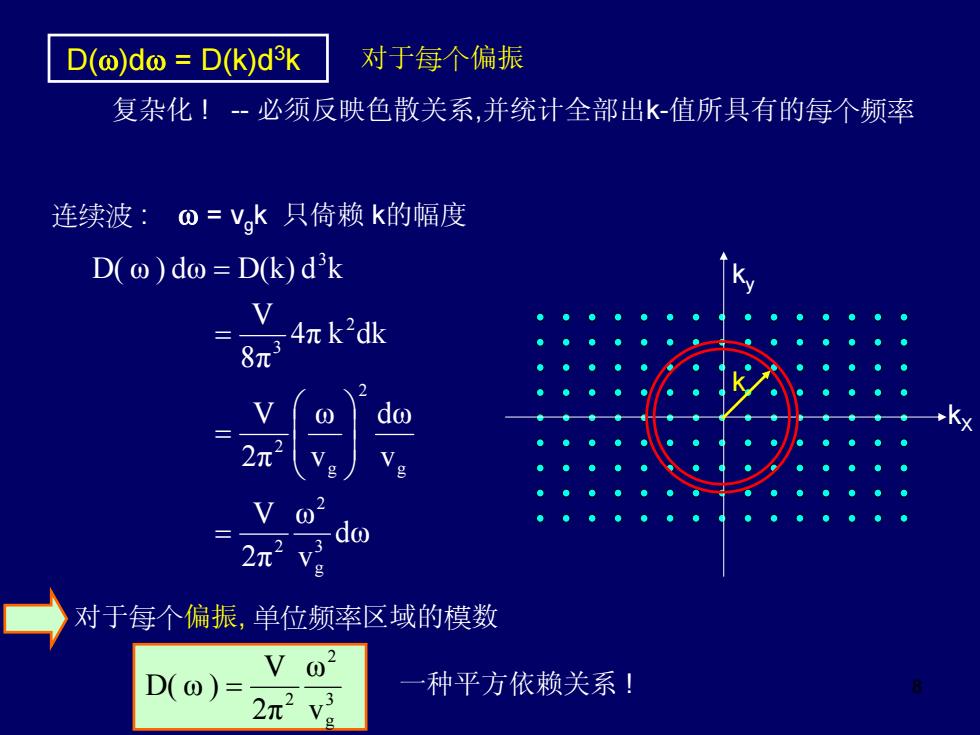
D(@)do=D(k)d3k 对于每个偏振 复杂化!-必须反映色散关系,并统计全部出k-值所具有的每个频率 连续波:O=V。k只倚赖k的幅度 D(@)do=D(k)dk 4元k2dk 8π V do 2r2 V do 3 对于每个偏振,单位频率区域的模数 V @2 D()= 2π2v 种平方依赖关系!
8 D(ω)dω = D(k)d3k 复杂化 ! - 必须反映色散关系,并统计全部出k-值所具有的每个频率 连续波 : ω = vgk 只倚赖 k的幅度 dω v ω 2π V v dω v ω 2π V π dkk 4 8π V D( ω ) ω kd D(k)d 3 g 2 2 g 2 g 2 2 3 3 = ⎟⎟⎠⎞ ⎜⎜⎝⎛ = = = 3 g 2 2 v ω 2π V D( ω ) = 对于每个偏振, 单位频率区域的模数 kX ky k 一种平方依赖关系 ! 对于每个偏振
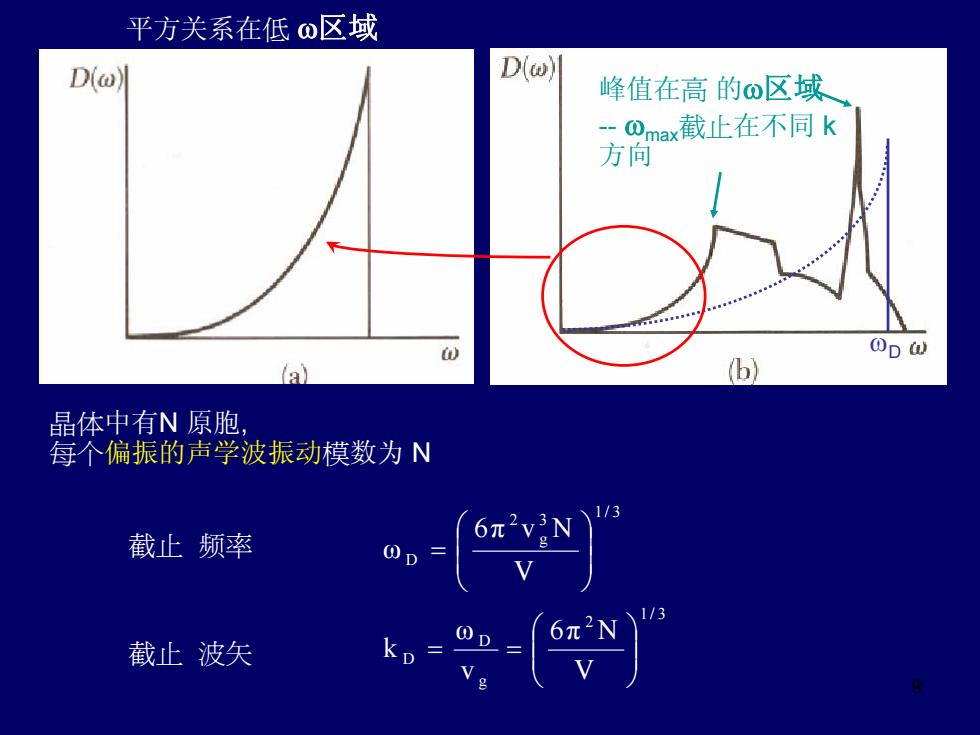
平方关系在低o区域 D(o) D(@ 峰值在高的o区域 Omax截止在不同k 方间 0D@ a】 (b) 晶体中有N原胞 每个偏振的声学波振动模数为N 截止频率 6π2N 截止波矢
9 平方关系在低 ω区域 ωD 峰值在高 的ω区域 - ωmax截止在不同 k 方向 晶体中有N 原胞, 每个偏振的声学波振动模数为 N 3/1 2 g D D 3/1 3 g 2 D V π N6 v ω k V π Nv6 ω ⎟⎟⎠⎞ ⎜⎜⎝⎛ == ⎟⎟⎠⎞ ⎜⎜⎝⎛ 截止 频率 = 截止 波矢
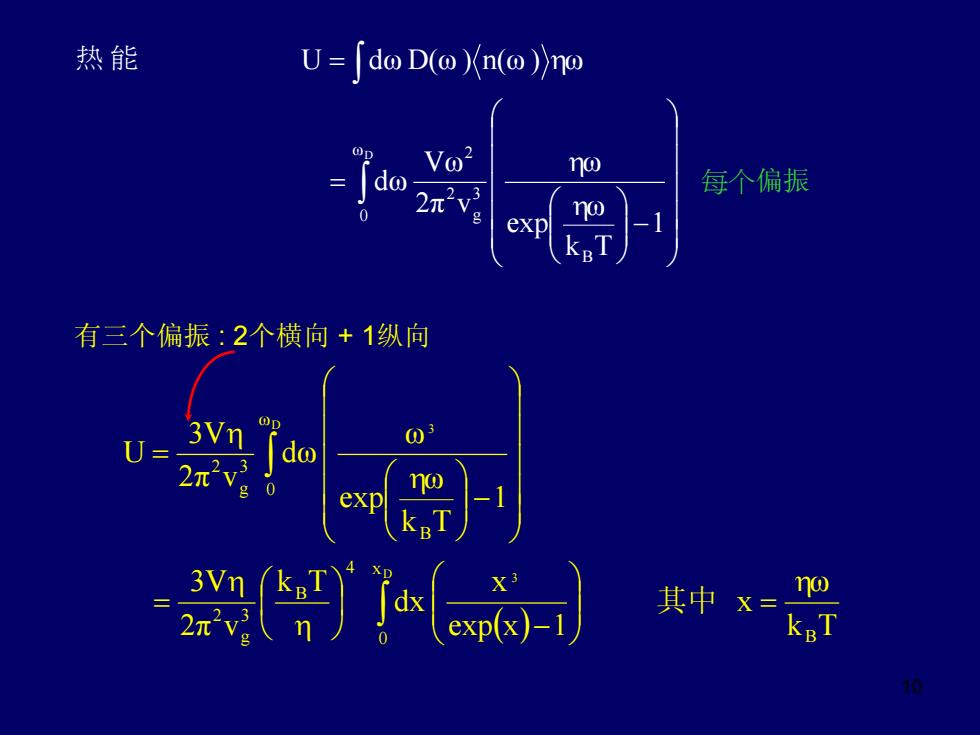
热能 U=do D(o)n())no Vo2 ro 每个偏振 no exp 有三个偏振:2个横向+1纵向 U= 3Vn @D do exp 其中x= no
10 ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ −⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = = ∫ ∫ 1 Tk ω exp ω π v2 V ω ω d U ω d ω ) D( ω ) n( ω B 3 g 2 ω 2 0 D η η 热 能 η 每个偏振 有三个偏振 : 2个横向 + 1纵向 ( ) Tk ω x 1xexp x dx Tk π v2 3V 1 Tk ω exp ω ω d π v2 3V U B x 0 4 B 3 g 2 B ω 0 3 g 2 D 3 D 3 η η η η η = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ −⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ∫ ∫ 其中