
第四章 留数定理及其应用
11 第四章 留数定理及其应用

§4.1留数留数定理 一、留数 根据单通区的科希定理,若f(z)在点x-b解析,为完全在 2-b<R内任意绕的简单闭合曲线,则: ∮,f恤=0 如果z=b是f(☑)的孤立奇点,为完全在z=b邻域0<z-b<R 内的任一绕的简单曲线,则: ∮nf(2)k≠0 留数定理将给处此积分的值, 若=b是函数f(z)的孤立奇点,则f(z)可在=b邻域内展成 罗朗级数: fa=2a,e-,0-bkR侧
22 §4.1 留数 留数定理 一、留数 ( ) 0 l f z dz = 如果z=b是f (z)的孤立奇点,l为完全在z=b邻域0<|z-b|<R 内的任一绕的简单曲线,则: 留数定理将给处此积分的值. 根据单通区的科希定理,若f(z)在点z=b解析,l为完全在 |z-b|<R内任意绕的简单闭合曲线,则: ( ) 0 l f z dz 若z=b是函数f (z)的孤立奇点,则f(z)可在z=b邻域内展成 罗朗级数: ( ) ( ) , (0 | | ) k k k f z a z b z b R =− = − −

设1为0<k-b<R内任一绕z=b的简单曲线,将上式两边沿逆 时针方向积分 ∮falk=a∮z-b血 根据第二章的讨论: k≠-1 9k=-1 ∮,f(z)=2mia1 定义:f(a在孤立奇点=b邻域内的罗朗展开式中(?-b)项的系 数叫做函数f②)在b的留数,记为: Ry6=ai∮dt=a (为邻域内任一沿正向绕的闭合曲线)
33 设l为0<|z-b|<R内任一绕z=b的简单曲线,将上式两边沿l逆 时针方向积分 b R l ( ) ( )k k l l k f z dz a z b dz =− = − 根据第二章的讨论: 0 1 ( ) 2 1 k l k z b dz i k − − = = − 1 ( ) 2 l f z dz ia = − 定义: f (z)在孤立奇点z=b邻域内的罗朗展开式中(z-b) -1项的系 数叫做函数f(z)在z=b的留数,记为: (为邻域内任一沿正向绕的闭合曲线) 1 1 Res ( ) ( ) 2 l f b f z dz a i = = −

1 例求函数f(z)= z3(z-2i) 在奇点z=0和z=2i上的留数. 解:f(z)把在=0邻域内展成罗朗级数 1111 f(z)= az-2i-2i 2i z3-2i0 (0<zk2) →Resf0)=a1=2i 8
44 例 求函数 3 在奇点z=0和z=2i上的留数. 1 ( ) ( 2 ) f z z z i = − 解:f (z)把在z=0邻域内展成罗朗级数 3 3 1 1 1 1 1 ( ) 2 2 1 2 f z z z z i i z i = = − − − 3 3 1 0 0 1 1 ( ) 2 2 (2 ) k k k k k z z z i i i − + = = = = − − (0 | | 2) z 1 3 1 Res (0) (2 ) 8 i f a i = = − = − −

把f()在-2邻域内展成罗朗级数,由于3在=2解析,所 以可在展成泰勒级数。 f(z)= 111 2-2i2=z-2e,+c(-20+c,亿-202+l (0Resf(b,)
55 把f (z)在z=2i邻域内展成罗朗级数,由于 在z=2i解析,所 以可在展成泰勒级数. 3 1 z 2 3 0 1 2 1 1 1 ( ) [ ( 2 ) ( 2 ) ] 2 2 f z c c z i c z i z i z i z = = + − + − + − − (0 | 2 | 2) − z i 1 0 3 2 1 Res (2 ) z i 8 i f i a c z − = = = = = 二、留数定理 设区域G的边界C为一分段光滑的简单闭合曲线. 若除有限 个孤立奇点bk,k=1,2,3,.,m外,函数在G内单值解析. 则: 1 ( ) 2 Res ( ) m k l k f z dz i f b = =

【证】以各奇点为圆心,以有限小的 半径作圆,把各奇点挖掉,挖掉各奇 点的区域为复连通区域,f(z)在该复连 通区域内解析,根据复通区域的科希 定理: 季e恤-季阳达+季e++fa =2πiResf(b)+2 ni Resf(b,)+.2πiResf(bm) =2πi∑Resf(b) k= 即f(z)沿闭曲线逆时针方向积分之值,等于f(z)在所包围 的区域内各奇点的留数之和乘于2π
66 【证】 以各奇点为圆心,以有限小的 半径作圆,把各奇点挖掉,挖掉各奇 点的区域为复连通区域,f(z)在该复连 通区域内解析,根据复通区域的科希 定理: 1 b 2 b k b m b l 1 l 2 l k l m l 1 2 ( ) ( ) ( ) ( ) l l l lm f z dz f z dz f z dz f z dz = + + + 1 2 2 Res ( ) 2 Res ( ) 2 Res ( ) m = + + i f b i f b i f b 1 2 Res ( ) m k k i f b = = 即f (z)沿闭曲线l逆时针方向积分之值,等于f (z)在l所包围 的区域内各奇点的留数之和乘于2i
三、无限远点为孤立奇点时的留数 仿照有限远奇点上的留数的定义, 可定义无限远点上的留数: Ref))=2元i∮,fad (1为z=∞邻域内任一沿正向绕 =∞的简单闭曲线),注意绕的 闭曲线的正方向应是顺时针方 向,如图. 在=∞邻域内的罗朗展开式为: )(r:k) 两边沿顺时针方向积分 ∮fe恤=】 a,ft=-立ak=2i
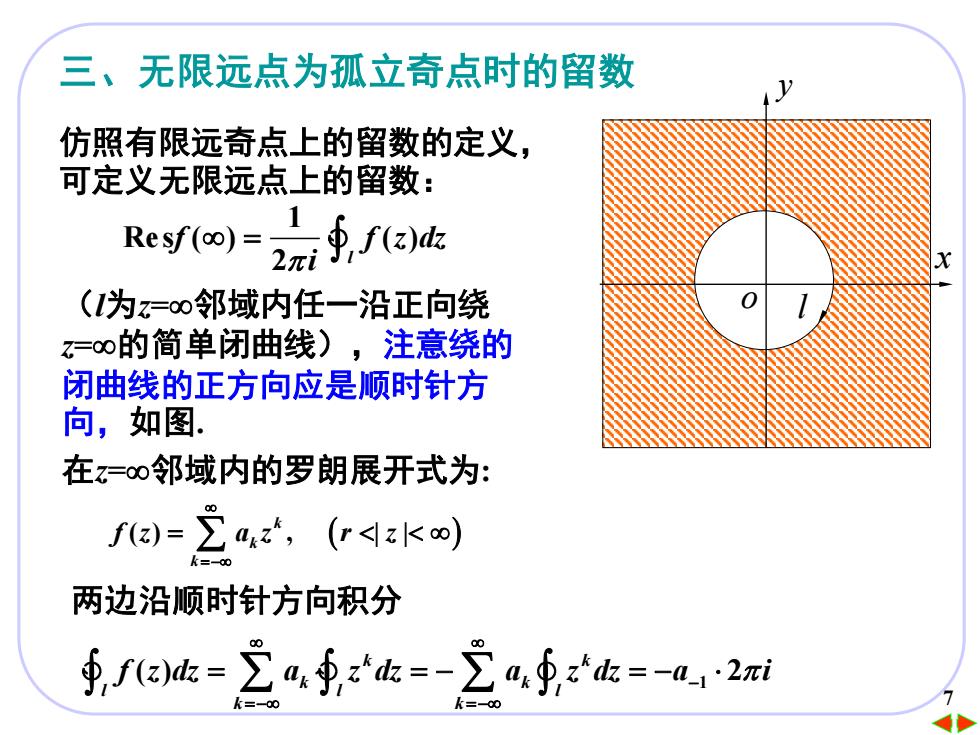
77 三、无限远点为孤立奇点时的留数 o x y l 仿照有限远奇点上的留数的定义, 可定义无限远点上的留数: 1 Res ( ) ( ) 2 l f f z dz i = (l为z=邻域内任一沿正向绕 z=的简单闭曲线),注意绕的 闭曲线的正方向应是顺时针方 向,如图. 在z=邻域内的罗朗展开式为: ( ) , | | ( ) k k k f z a z r z =− = 两边沿顺时针方向积分 1 ( ) 2 k k k k l l l k k f z dz a z dz a z dz a i − =− =− = = − = −

因此f(z)在=o的留数为f(z)在=oo邻域内的罗朗展开式 中z项的系数的a相反数,即 Resf(co)=-a_1 若f(z)在有限远的可去奇点邻域内的罗朗展开式中没有负 幂项,f()在有限远的可去奇点上的留数为零;若无限远 点为可去奇点时,f()在无限远点邻域内的罗朗展开式中 没有正幂项,但有负幂项,所以无限远点为可去奇点时, Resf(o)一般不为零. 四、推论 若函数f()在复平面上除有限个孤立奇点外解析,则函 数f(a)在各奇点(包括无限远点)上的留数和为零.此 定理称为留数和定理
88 因此f (z)在z=的留数为f (z)在z=邻域内的罗朗展开式 中z -1项的系数的a-1相反数,即 Res ( ) 1 f a = − − 若f (z)在有限远的可去奇点邻域内的罗朗展开式中没有负 幂项, f (z)在有限远的可去奇点上的留数为零;若无限远 点为可去奇点时,f (z)在无限远点邻域内的罗朗展开式中 没有正幂项,但有负幂项,所以无限远点为可去奇点时, Res f ()一般不为零. 四、推论 若函数f (z)在复平面上除有限个孤立奇点外解析,则函 数f (z)在各奇点(包括无限远点)上的留数和为零. 此 定理称为留数和定理

【证】 设闭曲线把复平面内所有的有限远的孤立奇点都包围 在内,则: ∮,f(z)k=2πi∑Res/(b:) 无限远点的留数为:∮,f(z)k=2πiResf(o) ·b2 b 两式相加,得: ∮,fzk+∮fz)k=2πi∑Res(b:)+Resf(o川 因此 Res()Rev() 若f()在某一奇点上留数不好求,可以先计算其他各点的留 数,再用留数和定理求出该点的留数
99 【证】 设闭曲线l把复平面内所有的有限远的孤立奇点都包围 在内,则: m k=1 ( ) 2 Res ( ) k l f z dz i f b = 无限远点的留数为: ( ) 2 Res ( ) l f z dz i f = 两式相加,得: m k=1 ( ) ( ) 2 [ Res ( ) Res ( )] k l l f z dz f z dz i f b f + = + m k=1 Res ( ) Res ( ) 0 k 因此 f b f + = 1 b 2 b 3 b m b l 若f (z)在某一奇点上留数不好求,可以先计算其他各点的留 数,再用留数和定理求出该点的留数

§4.2留数的计算方法 f(亿)在奇点上的留数可根据留数的定义,将函数fz)在奇 点=b邻域内展成罗朗级数: Resf(b)=a_ 41为该罗朗展开式中(ab)项的系数. 如果要求在f(z)无限远点上的留数,可将f(z)在邻域内展 成罗朗级数, Res f(oo)=-a_ 1为该罗朗展开式中z项的系数. 从一般原则来说,只要在以奇点为圆心的圆环域上把函数 展开为罗朗级数,取它的负一次幂项目系数就行了,但如 果能不作罗朗展开而直接算出留数,计算工作量将减轻不 少。在应用留数定理计算回路积分时,往往会遇到在极点 上留数的计算. 10
1010 §4.2 留数的计算方法 f (z)在奇点上的留数可根据留数的定义,将函数f(z)在奇 点z=b邻域内展成罗朗级数: Res ( ) 1 f b a = − a-1为该罗朗展开式中(z-b) -1项的系数. 如果要求在f(z)无限远点上的留数,可将f (z)在邻域内展 成罗朗级数, Res ( ) 1 f a = − − a-1为该罗朗展开式中z -1项的系数. 从一般原则来说,只要在以奇点为圆心的圆环域上把函数 展开为罗朗级数,取它的负一次幂项目系数就行了,但如 果能不作罗朗展开而直接算出留数,计算工作量将减轻不 少。在应用留数定理计算回路积分时,往往会遇到在极点 上留数的计算