面井京机女飘人大子 21西体姓◆物香选格运 2.1晶体结合的善造描述 第二幸围体中的原子能合 化学使(chemical bond) 2.1晶体结合的普流描述 2.2共价晶体 2.3高子晶体 分子轨道法(Molecular Orbital method) 2.4分子于晶体、金属及氩能晶体 2.5原子的负电世不晶体地合规律 Atomic Orbitals) 的邦家机堂积天大子 21品体地个的华电装适 ©心外家机堂税人大子 H,分子:轨道 轨道与 不轨道 的北家机空航人大子 西共家机实积天大行 2、价镜法(Valence bond method) 二晶体的分类 根据电子在空间的分布、健形成的物理起 潭和所沙及的健的性质,将化学使分成五 种类型:离子健、共价能、分子健、氢 镜、金属健。前四种形成的国体一般为 鲍嫌体,后一种形成导体(即金属)
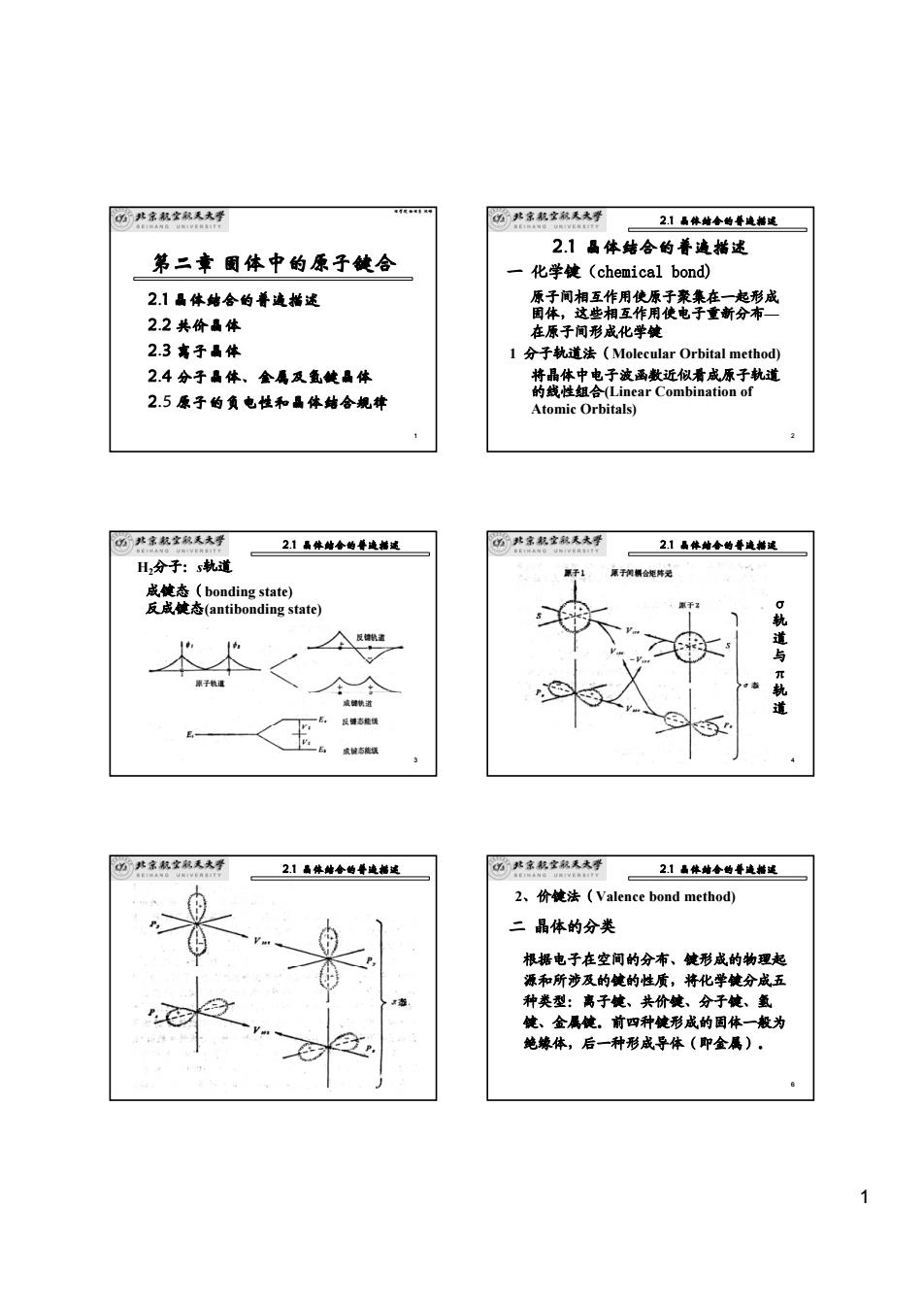
1 1 理学院 物理系 沈嵘 第二章 固体中的原子键合 2.1 晶体结合的普遍描述 2.2 共价晶体 2.3 离子晶体 2.4 分子晶体、金属及氢键晶体 2.5 原子的负电性和晶体结合规律 2 2.1 晶体结合的普遍描述 一 化学键(chemical bond) 原子间相互作用使原子聚集在一起形成 固体,这些相互作用使电子重新分布— 在原子间形成化学键 1 分子轨道法(Molecular Orbital method) 将晶体中电子波函数近似看成原子轨道 的线性组合(Linear Combination of Atomic Orbitals) 2.1 晶体结合的普遍描述 3 H2分子:s轨道 成键态(bonding state) 反成键态(antibonding state) 2.1 晶体结合的普遍描述 4 σ 轨 道 与 π 轨 道 2.1 晶体结合的普遍描述 5 2.1 晶体结合的普遍描述 6 2、价键法(Valence bond method) 二 晶体的分类 根据电子在空间的分布、键形成的物理起 源和所涉及的键的性质,将化学键分成五 种类型:离子键、共价键、分子键、氢 键、金属键。前四种键形成的固体一般为 绝缘体,后一种形成导体(即金属)。 2.1 晶体结合的普遍描述
21备蛛雄◆的普地描越 21晶保地◆的平地描速 三晶体的结合能(binding energy) 88 88 1瓷义 处于穗定状态的晶体,其总能量(动能 合能 T=8w- 。 21西件特◆的年选增远 21品体地◆的普成制道 动能 其它体相 设品体中两粒子的互作用势能为:风,) 陪等能量。 由N个粒子组成的晶体总互作用势能为: 以w为泰考能位:可=-司 品=∑2,)j 2总相互作用能(品格能)与站合能 R)=R) 经典双粒子相互作用摸型:花品体中总的 含8好 求出晶体的总势能. 5-2o加-20 西非家款含积人大手 2.1高体他合的普造着减 北家航空机人太香 21昌体始本的善成据成 3两粒子间的相互作用力和相互作用能 由)可计算两粒子 间的互作用力: 2 -0当 引力=斥力 一定 两子的相互作用势 是子香农两散子 0)=-+ 当=-Q.=0<>0斥力 有救吸引力最大 r>,f)k0引九
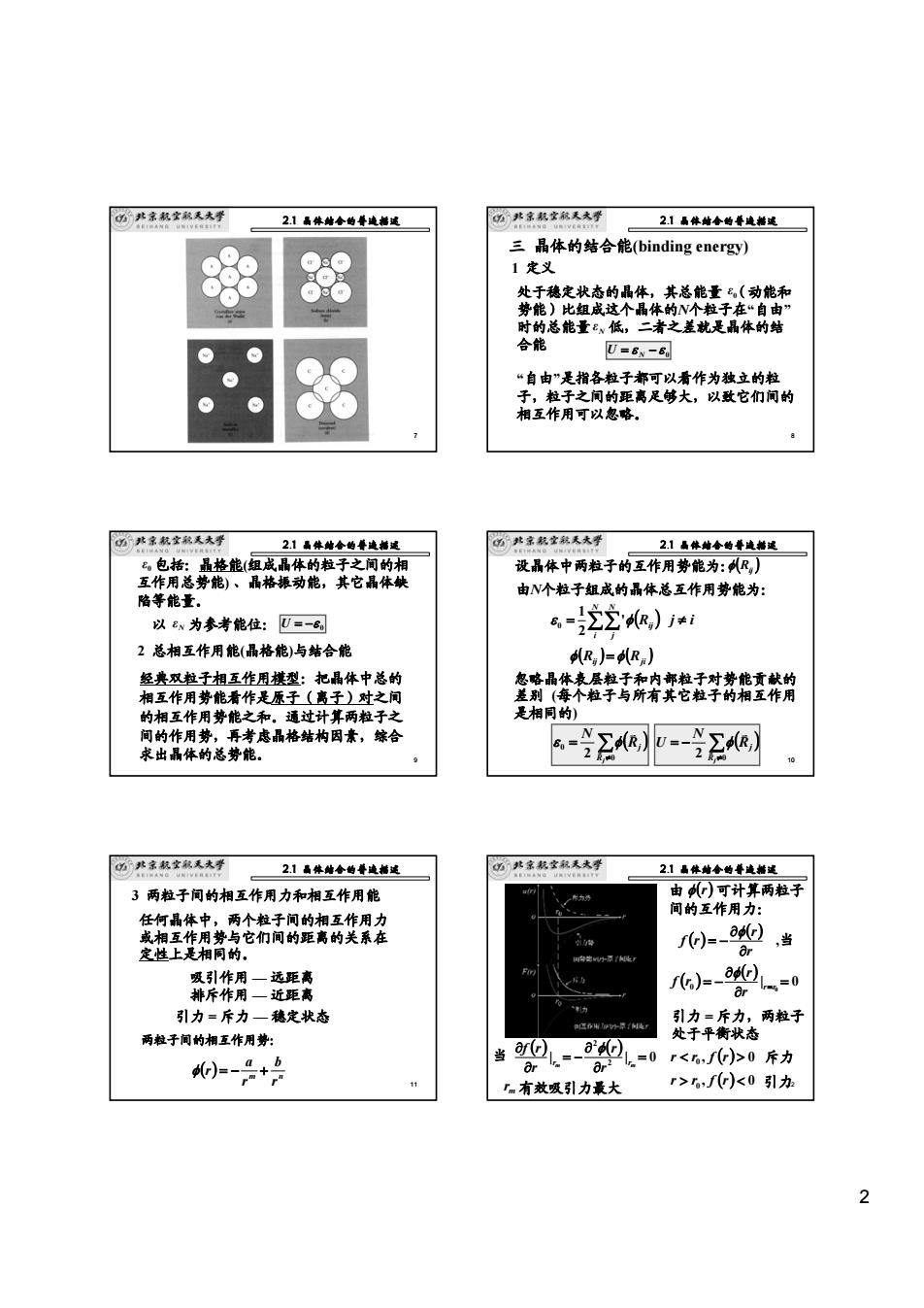
2 7 2.1 晶体结合的普遍描述 8 三 晶体的结合能(binding energy) 1 定义 “自由”是指各粒子都可以看作为独立的粒 子,粒子之间的距离足够大,以致它们间的 相互作用可以忽略。 处于稳定状态的晶体,其总能量 (动能和 势能)比组成这个晶体的N个粒子在“自由” 时的总能量 低,二者之差就是晶体的结 合能 0 ε Nε 0 = ε − ε U N 2.1 晶体结合的普遍描述 9 2 总相互作用能(晶格能)与结合能 经典双粒子相互作用模型:把晶体中总的 相互作用势能看作是原子(离子)对之间 的相互作用势能之和。通过计算两粒子之 间的作用势,再考虑晶格结构因素,综合 求出晶体的总势能。 包括:晶格能(组成晶体的粒子之间的相 互作用总势能) 、晶格振动能,其它晶体缺 陷等能量。 0 ε 以 为参考能位: Nε 0 U = −ε 2.1 晶体结合的普遍描述 10 由N个粒子组成的晶体总互作用势能为: = ∑∑ ( ) N i N j φ Rij ε ' 2 1 0 j ≠ i ( ) ( ) φ Rij = φ Rji 忽略晶体表层粒子和内部粒子对势能贡献的 差别 (每个粒子与所有其它粒子的相互作用 是相同的) ∑ ( ) ≠ = 0 0 2 Rj Rj N v v ε φ 设晶体中两粒子的互作用势能为:( ) φ Rij ∑ ( ) ≠ = − 2 Rj 0 Rj N U v v φ 2.1 晶体结合的普遍描述 11 3 两粒子间的相互作用力和相互作用能 任何晶体中,两个粒子间的相互作用力 或相互作用势与它们间的距离的关系在 定性上是相同的。 吸引作用 — 远距离 排斥作用 — 近距离 引力 = 斥力 — 稳定状态 两粒子间的相互作用势: ( ) m n r b r a φ r = − + 2.1 晶体结合的普遍描述 12 由 可计算两粒子 间的互作用力: φ(r) ( ) ( ) r r f r ∂ ∂ = − φ ( ) ( ) | 0 0 0 = ∂ ∂ = − r=r r r f r φ ,当 引力 = 斥力,两粒子 处于平衡状态 r 0 斥力 r > r0 , f (r) < 0 引力 ( ) ( ) | | 0 2 2 = ∂ ∂ = − ∂ ∂ rm rm r r r f r φ 当 rm 有效吸引力最大 2.1 晶体结合的普遍描述

22善0晶体 22共骨4单 2.2共价晶体 二氢分子的价使理论 特征 结合力:共价纯填满原于的外电子壳层的 方式之一,相邻两个原子各出一个电于为 两个原子实共用。 晶体结构:地和性,方向性一原子能够形 成共价健的数目不会超过4个,配位数低。 晶体特征:高这点、硬度/碗。导电性码 小位,由此处对应的能量可算出重分 可北家机士税人大子 22热件品件 北家积立税人水手 224体 原来不是满先层的两个氢原于,被此占用 三轨道杂化理论 方的自荧 的 金刚石:四个等同的价能 ℃版于.12222n2 男木自我济 的电于即形成一 的北家航空就无大子 22共告晶件 高北家航宝礼天大雪 22桥昌 2态与2p态接近,一个2s电于澈发到2印态: )-+p.+p,+n》 1s2s2pp,p,基)→122p,卫.撒发态) -+p.l,-》 四个未配对电子 -)-.,H》 四个健混合“起来重新组成四个等价轨道 -p,》 一由原子的s,P,P:态选加而成. 电子云集中在四面体的四个顶角方向。原来 杂化轨道(hybrid orbital). 在2s,20上的四个电子分别在杂化轨道上成 为未配对电子,可以在四面体顶角方向上形 成4个等价的共价健
3 13 2.2 共价晶体 一 特征 结合力:共价键(填满原子的外电子壳层的 方式之一),相邻两个原子各出一个电子为 两个原子实共用。 晶体结构:饱和性,方向性⇒原子能够形 成共价键的数目不会超过4个,配位数低。 晶体特征:高熔点、硬度/脆,导电性弱 2.2 共价晶体 14 二 氢分子的价键理论 曲线Ⅰ:两个氢原子的1s电子自旋方向相同;在 任何原子间距时总是排斥的,不能结合成分子。 曲线Ⅱ:1s电子自旋方向相反,在 处有一个极小值。由此处对应的能量可算出氢分 子的结合能。 RAB a0 =1.518 2.2 共价晶体 15 原来不是满壳层的两个氢原子,彼此占用 了对方的自旋相反的1s电子后,都具有类氦 的稳定的封闭壳层,结合成氢分子-氢原 子以共价键方式结合成分子的物理本质。 价键理论:原子中未成对的电子,可以和 另一个原子中一个自旋方向相反的未成对 电子配对,配对的电子即形成一个共价键 ⎯⎯电子配对理论 2.2 共价晶体 16 三 轨道杂化理论 金刚石:四个等同的价键 C 原子: 1s22s22p2 只有两个未配对 电子 2.2 共价晶体 17 2s态与2p态接近,一个2s电子激发到2p态: 1s22s22px 1py 1pz 0(基态) →1s22s12px 1py 1pz 1(激发态) ——四个未配对电子 。 四个键“混合”起来重新组成四个等价轨道— —由原子的s,px,py,pz态迭加而成。 ——杂化轨道(hybrid orbital) 。 2.2 共价晶体 18 ( ) x y z h = s + p + p + p 2 1 1 ( ) x y z h = s + p − p − p 2 1 2 ( ) px py pz h = s − + − 2 1 3 ( ) x y z h = s − p − p + p 2 1 4 电子云集中在四面体的四个顶角方向。原来 在2s,2p上的四个电子分别在杂化轨道上成 为未配对电子,可以在四面体顶角方向上形 成4个等价的共价键。 2.2 共价晶体
22共价品单 子插 及管形盏桑化轨道时。建质子能量比基杰豪 2.3喜子晶体 一特征 大于形成杂化制 站合力:离子正、负离子间的静电相五 体系的能 作用) 晶体姑构:不等径球尽可能紧密的堆和。 例:NaCL CsC1 品休精征:结构穗定、更度高、点高、 子电性能差. 西北家机宝机无大手 23高号4集 面非家机宝税人大子 23有号品华 作骨建任一个高子不系个离子同的相江 两离子间的库企作: R,)= e 后”二丹楼} M体由N个原子姐成,总的互作用能: R:离子对间的距离 6z,制 其它排乐整:是 西邦家航金机人大行 23*子4体 西北家机空秋人太于 2.3有子品# 最近离子间距为RR)=P,R 2马德隆常数 。动别 -号一仅由品体结构决定 令a-Z±2-一Madell cota 第一次计算由Madellu 平均一对离于1分子) 例1正负一价高子姐成的一单晶格
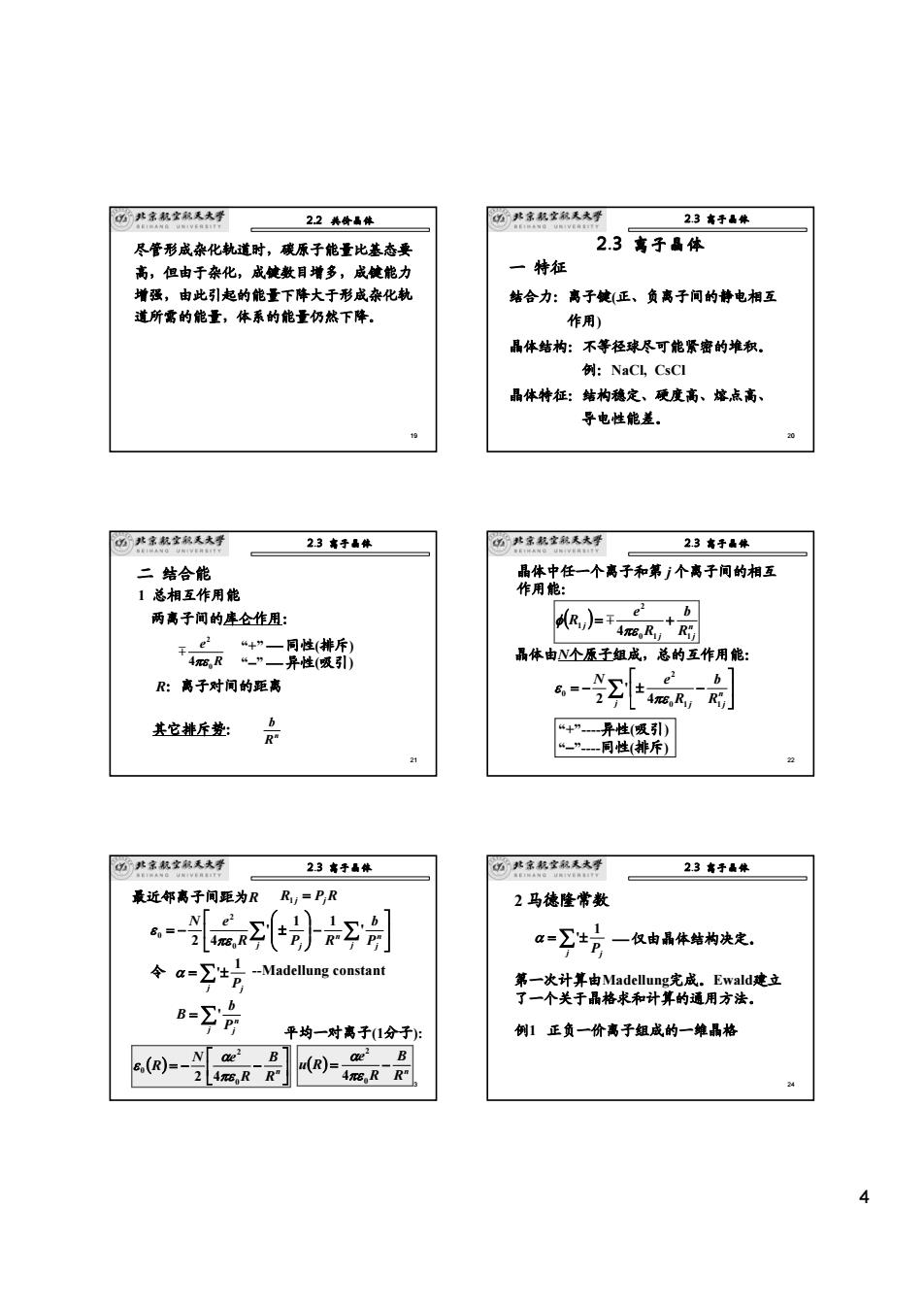
4 19 尽管形成杂化轨道时,碳原子能量比基态要 高,但由于杂化,成键数目增多,成键能力 增强,由此引起的能量下降大于形成杂化轨 道所需的能量,体系的能量仍然下降。 2.2 共价晶体 20 2.3 离子晶体 一 特征 结合力:离子键(正、负离子间的静电相互 作用) 晶体结构:不等径球尽可能紧密的堆积。 例:NaCl, CsCl 晶体特征:结构稳定、硬度高、熔点高、 导电性能差。 2.3 离子晶体 21 二 结合能 1 总相互作用能 两离子间的库仑作用: R e 0 2 4πε m “+” ⎯ 同性(排斥) “−” ⎯ 异性(吸引) 其它排斥势: n R b R:离子对间的距离 2.3 离子晶体 22 晶体中任一个离子和第 j 个离子间的相互 作用能: ( ) n j j j R b R e R 0 1 1 2 1 4 = + πε φ m 晶体由N个原子组成,总的互作用能: ∑ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − ± − j n j R j b R N e 0 1 1 2 0 4 ' 2 πε ε “+”-异性(吸引) “−”-同性(排斥) 2.3 离子晶体 23 最近邻离子间距为R R1 j = PjR ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = − ∑ ∑ ± j j n j n j P b R P R N e ' 1 1 ' 2 4 0 2 0 πε ε 令 = ∑ ± j Pj 1 α ' = ∑ j n Pj b B ' ( ) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − − n R B R N e R 0 2 0 2 4πε α ε -Madellung constant ( ) n R B R e u R = − 0 2 4πε α 平均一对离子(1分子): 2.3 离子晶体 24 2 马德隆常数 第一次计算由Madellung完成。Ewald建立 了一个关于晶格求和计算的通用方法。 = ∑ ± j Pj 1 α ' ⎯ 仅由晶体结构决定。 例1 正负一价离子组成的一维晶格 2.3 离子晶体

回共条款士秋人大子 23寿子4体 23有子4保 9日里69g” a-片】 R风=PRa=y4司 南0+动-受5-子 “4”相异离子的贡献“”相同离子的贡献 以某一离子为原点,左右对称排列 令a12=1-时 a=2h2 2C:P=3+ 防北家积宝税人太子 23客子西体 23者安西体 例2正负一价离子姐成的二帷正方格子 P,=+ R一最近你离子间厘, P年个离 其它离子坐标: 000-09 近第10)4+) (R.nR) 次近绍 第三近第(2,0 R,=√所+所R=PR 第四近第(2,)8(+)52 0 第五近邹(2,24曰224 000-0 防北家航空就无大子 2.3高予山体 高北家机空礼人太子 23嘉子品体 例3正负一价离子组成的三维正方格子 漫近都高子间距, 每资子 最近邻6+)1 1/2 其它离于坐标:(n.R.nR.m,R) 次近邻12-)21/4 第三近+)318 R,=√G+店+所R=P,R P,=+所+居 扩大计算的选取花国,得到更精确的口
5 25 R R1 j = PjR = ∑ ± j Pj 1 α ' PA = 1 PB = 2 PC = 3 ⊕ − ⊕ − ⊕ − ⊕ R C C B A A B “+”-相异离子的贡献 “–”-相同离子的贡献 以某一离子为原点,左右对称排列 2A: “+” 2B: “–” 2C: “+” . 2.3 离子晶体 26 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − + − +L 4 1 3 1 2 1 α 2 1 ( ) + = − + − +L 2 3 4 ln 1 2 3 4 x x x x x x = 1 = − + − +L 4 1 3 1 2 1 ln2 1 α = 2ln2 由 令 2.3 离子晶体 27 例2 正负一价离子组成的二维正方格子 (n R n R) 1 2 , R ⎯最近邻离子间距, 其它离子坐标: R j = n + n R = PjR 2 2 2 1 1 2.3 离子晶体 28 2 2 2 Pj = n1 + n 第五近邻 第四近邻 第三近邻 次近邻 最近邻 每个离子 贡献 坐 标 离子数 Pj 2 5 2 2 1 2 1 2 1 4 4(+) 1 1 1 2 4(−) 4(−) 4(−) 8(+) (1,0) (1,1) (2,0) (2,1) (2,2) 4 2 2 4 2 5 8 2 2 4 2 4 4 × + − × α = − − ≈ 1.6069 2.3 离子晶体 29 例3 正负一价离子组成的三维正方格子 (NaCl结构) R -最近邻离子间距, 其它离子坐标:(n R n R n R) 1 2 3 , , R j = n + n + n R = PjR 2 3 2 2 2 1 1 2 3 2 2 2 Pj = n1 + n + n 2.3 离子晶体 30 第三近邻 次近邻 最近邻 每个离子 贡献 离子数 Pj 6(+) 1 2 12(−) 2 1 4 8(+) 3 1 8 1 1.457 8 3 8 4 2 12 2 6 α = − + = 扩大计算的选取范围,得到更精确的 α 2.3 离子晶体

23子佛 23子插 香息,奉个原他体积 +. 得:B=心 弃经r丽下修6,对 P◆△V=-Aa 瓜:P-影0 华性关系:户-水二,怎休软弹性横更 西非家机士机人大子 23有号4排 23者子西体 ) N个原胞(2N个高子)的势能: 将P=0代入- -N.R )。鬥 NaCI品体体积:V=2NR -{服。 格B-代入→ (=)意盖- 西非家款含积人大手 23客子4体 北家航空秋人太香 23高子备保 会-) 4结合能 e-n高 用()=+=· n-1+2K万 确定的及来因=需心 >个原子组成晶体的站合能: 凡←晶格常数,实验】 a←晶体几何站构 -小-周 K←实验 -)
6 31 3 B和n的确定 由平衡条件: 0 d 2 4 d 0 0 2 1 0 2 0 = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ = − − + ⎠ ⎞ ⎜ ⎝ ⎛ + R n R R nB R N e R πε ε α 得: 1 0 0 2 4 − = n R n e B πε α :最近邻离子间的平衡距离。可通 过测定晶格常数确定。 R0 n:描述离子间由于电子云重叠而产生 排斥作用的参数,可与晶体的体积弹性 模量建立联系。 2.3 离子晶体 32 在压强P作用下,晶体体积增加 ,对外 作功: ∆V 晶体体积V,包含N个原胞,每个原胞体积v, 每个原胞的平均势 u(v) = Nu(v) 0 ε V = Nv 压强: 0 P • ∆V = −∆ε v u V P ∂ ∂ = − ∂ ∂ = − 0 ε 弹性关系: , V V P K ∆ = − K-体积弹性模量 2.3 离子晶体 33 V T P K V ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = − 将 代入: V P ∂ ∂ = − 0 ε 0 2 0 2 0 V V K V ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ = ε NaCl晶体体积: 3 V = 2NR 0 0 2 0 2 0 2 0 2 0 9 2 1 V R V NR R K V ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ × = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ = ε ε 2.3 离子晶体 34 ( ) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + = − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ −1 0 0 2 3 0 2 0 2 1 2 0 n R R e n n B R N R πε ε α N 个原胞(2N个离子)的势能: 1 0 0 2 4 − = n Rn e B πε α 将 代入: ( ) n e R N R R = − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ 1 4 0 2 3 0 2 0 2 0 πε ε α ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − − n R B R e N 0 2 0 4πε α ε 2.3 离子晶体 35 ( ) 1 9 2 4 1 0 2 3 0 0 • − × = n e R N NR K πε α ( ) 4 0 0 2 72 1 R e K n πε α = − K e R n 2 4 72 0 0 1 α πε = + R0 α K n B ←晶格常数,实验 ←晶体几何结构 ←实验 2.3 离子晶体 36 ( ) ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − = − R n N e U R 1 1 2 4 0 0 2 0 0 πε α ε 4 结合能 0 2 4 0 0 2 1 0 2 0 = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ = − − + ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + R n R R nB R N e R πε ε α 用 R0 1 0 0 2 4 − = n Rn e B πε α 确定的 和 代入 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = − R n e u 1 1 4 0 0 2 πε α N个原子组成晶体的结合能: 2.3 离子晶体

2.3高于4单 23高子4单 三离子半径 朵斯季径按健型:共价,高子,花倦元 量子力学观点:不能严格定义分子或国体中 冬帝清骨原有夜年狗影绣平大旅肆 的半径是位定的。 共价半径 原子核及周国电子之刚球 然李拉品修能原子中青间距 原子球大小赞簧原子种凭成几有为型 可北家机士税人大子 23率号4排 北家积立税人水手 23客子插米 金属的原子半径 离子半径 金属元素正离子作等径国球 原子半径为相师两原子核间距的一半. 蒸于电子构考虑推算离子半径 范德瓦尔斯半径 福视以腐隆子奔教盐苹合子网 单价半径:R= 防北家航空就无大子 23车子4体 北家机空和人大手24子品华。4又鱼被品体 :NaF离子间距231AS=452 2.4分子晶体、金属及直能品体 R1n短Ru- 一分子晶体 R,-R,- 1特点 结合力:范德瓦尔斯力,结构单元醉时 R+R-=2.31A 偶极矩的相互作用 R=095AR=136A 多价:R,=R刀)刀-离于的价数
7 37 三 离子半径 量子力学观点:不能严格定义分子或固体中 原子的大小。 原子半径:描述原子和离子大小的经典 概念。 统计平均的角度 :每个原子周围有一定 数量的电子。 原子核及周围电子 刚球 键型 周围原子种类及几何构型 “原子球”大小 2.3 离子晶体 38 忽略其他原子和几何构型对原子大小的影 响,属同一价键的不同化合物中,各原子 的半径是恒定的。 同一原子,按键型:共价,离子,范德瓦 尔斯半径 共价半径 元素共价晶体: 共价半径=1/2成键原子平衡间距 2.3 离子晶体 39 金属的原子半径 金属晶体—金属元素正离子作等径圆球 密堆积而成。 原子半径为相邻两原子核间距的一半。 分子间以范德瓦尔斯力结合时,分子间 相互接触的原子所表现出的半径。 范德瓦尔斯半径 2.3 离子晶体 40 离子半径 由晶体衍射精确测定正负离子的平衡间距 和电子密度,然后划分正负离子半径 Goldschmidt Pauling Zachariasen Z S C R − 1 = 基于电子结构考虑推算离子半径 单价半径: C—由外层电子主量子数所决定的常数 S—屏蔽常数 Z—原子序数 2.3 离子晶体 41 例:NaF离子间距 2.31 Å S = 4.52 6.48 , 11 4.52 1 C R R Na Na = − + ∝ + 4.48 , 9 4.52 1 C R R F F = − − ∝ − o + + − = 2.31A Na F R R o + = 0.95A Na R o − = 1.36A F R 多价: 2 ( ) 1 1 − − = n Rη Rη η-离子的价数 2.3 离子晶体 42 2.4 分子晶体、金属及氢键晶体 一 分子晶体 1 特点 结合力:范德瓦尔斯力,结构单元瞬时 偶极矩的相互作用 晶体结构:最密排方式 特征:熔点低,硬度小 2.4 分子晶体、金属及氢键晶体

24分手晶体,金4灭直就品体 24◆子高除、会4及重做西蜂 2范德瓦尔斯力 >非板性分子:醉时偶极矩间的相互作用 第一个原子的醉时偶板矩印,在R处的电场: R 的感生偶矩; 3分子晶体的结合能 Pa-af- 范德瓦尔斯力-吸引势:工 两偶板矩之门的互作用能 排斥势-Pauli exclusion principle: . 经验持斥势:匹西 西北家积实机天大行24命子4体.金4天氨做通体 面水家机实积天水子24牛4体4人色能4体 ()一对原子间的作用势 】 我京+日 >当R=gR)=0 令-份-品→ 。表示两个原子间梦能为率时的距高 R<σ势能曲线意时上升排斥作用范国, 同 由1。=0,得R=2。R,)-。 勒钠-球斯6-12势(Leanard-Jones6-12 potential) 。与两原于间的平衡距离有送 :两个原子的站合能或离解能 西非家款含积人大手 24女子晶保,金属发重做晶体 北家航空秋人大季 24套子昌体.查昌发重被体 (2)分子晶体晶格能 由N个分子(原子)组成分于晶体,总势能 ◆4-习证4=习可仅与皓构有关。 =x →-44- R-最近邻分子(原子)间距,R,=PR (③)晶格常数及宏观力学量 平均到每个分子(略去负号): 平衡时分子(原子)间距
8 43 2 范德瓦尔斯力 ¾非极性分子:瞬时偶极矩间的相互作用 第一个原子的瞬时偶极矩pe1在R处的电场: 3 E ∝ pe1 R v 第二个原子产生的感生偶极矩: 3 1 2 R p p E e e α = α = 两偶极矩之间的互作用能 6 2 1 3 1 2 R p R pe pe α e = 2.4 分子晶体、金属及氢键晶体 44 ¾极性分子:固有电偶极矩间作用势 固有偶极矩与感生偶极矩间 6 1 R ∝ 3 分子晶体的结合能 范德瓦尔斯力-吸引势: 6 1 R ∝ 排斥势-Pauli exclusion principle: 12 1 R 经验排斥势:∝ 2.4 分子晶体、金属及氢键晶体 45 (1) 一对原子间的作用势 ( ) 6 12 R b R a φ R = − + b a a b 4 , 1 6 2 ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ σ = ε ( ) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ = 12 6 4 R R R σ σ φ ε 令 勒纳-琼斯6-12势(Lennard-Jones 6-12 potential) 2.4 分子晶体、金属及氢键晶体 46 ¾ 当 时, R = σ φ(R) = 0 σ 表示两个原子间势能为零时的距离。 R < σ 势能曲线急剧上升 排斥作用范围。 ( ) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ = 12 6 4 R R R σ σ φ ε ( ) | 0 0 = ∂ ∂ R R φ R σ 1 6 R0 = 2 φ( ) = −ε ¾由 ,得 R0 σ 与两原子间的平衡距离有关 ε 两个原子的结合能或离解能 2.4 分子晶体、金属及氢键晶体 47 (2) 分子晶体晶格能 由N个分子(原子)组成分子晶体,总势能 ∑ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = j R j R j N 6 1 12 1 0 ' 4 2 σ σ ε ε R-最近邻分子(原子)间距, R1 j = PjR ( ) ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ∑ ∑ 6 12 2 ' ' j j PjR PjR u R σ σ ε 平均到每个分子(略去负号): 2.4 分子晶体、金属及氢键晶体 48 ( ) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ = 6 6 12 2 12 R A R u R A σ σ ε = ∑ j Pj A12 12 1 ' = ∑ j Pj A6 6 1 令 ' 仅与结构有关。 (3) 晶格常数及宏观力学量 0 12 6 | 2 0 0 7 6 13 6 12 12 0 = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = − + ∂ ∂ R R R A R N A R σ σ ε ε ¾平衡时分子(原子)间距 由 2.4 分子晶体、金属及氢键晶体

西外条款含税人大子24参于A体4天线a体 画邦京称含秋人大行24会好4体会4美做4体 年飞-安的-4地款 体弹摸量 创:面心立方情性元素品体,原胞体积 >结合能 A=14.45392A=1213188 平衡时活体的多务能:6仅)-瓷N R球近你原子同距。=队一号 站合常:-6)小一器N 补合于(傅)的手墙士一兴。 晨告 西非京机女机人大行24子4体.合区能a体 面并家积含税人大子24好体、合4人能4体 二量子品体 三金属晶体 轻典国体:定造 站合力:原于实和价电子云间的静电库仑力, 固体气:原子有很大的零点运动振橘,可 体站构:个金 以隧穿到近师的格点上,在晶体中的位重 》同一种金属原手等 发生退定城,从而不可分辨,称为重于晶 方, 在结合能计算时,章点远动能不能略去。 蜜度泛函理论:结合能1~5cV原子 的北家航宝飘无大子 四氨使晶体 原子的价电子与其它原子形成价能 预。解释未些“精细的结合种性时起重要 布近 游众打:盖健值原子同时未共它两个承子 与马一小电黄性献火的原子和陆合。 使的特点来源于氯原子的特性 >价电子电离能高(13.6o)0Wa原子5.14om >保内西实地 >离于实很小
9 49 σ 1 6 6 12 0 2 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = A A 得:R ⇒ 晶格常数 ¾ 结合能 平衡时晶体的总势能: ( ) N A A R 12 2 6 0 0 2 ε ε = − ( ) N A A U R 12 2 6 0 0 2 ε = −ε = 每个分子(原子)的平均能量: 12 2 6 2A A u ε = 结合能: 2.4 分子晶体、金属及氢键晶体 50 ¾ 体弹模量 例:面心立方惰性元素晶体,原胞体积 4 3 0 a v = R最近邻原子间距 2 2 , 3 0 R a = R v = 2 3 0 R V = Nv = N 5 2 12 6 2 3 12 0 2 0 0 4 9 2 0 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ = A A A NR R K R σ ε ε A6 = 14.45392 A12 = 12.13188 ε σ ε σ 0 3 0 0 75 8.6 1.09 = = − = K u R 2.4 分子晶体、金属及氢键晶体 51 二 量子晶体 经典固体:定域 固体氦:原子有很大的零点运动振幅,可 以隧穿到近邻的格点上,在晶体中的位置 发生退定域,从而不可分辨,称为量子晶 体。 在结合能计算时,零点运动能不能略去。 2.4 分子晶体、金属及氢键晶体 52 三 金属晶体 结合力:原子实和价电子云间的静电库仑力. (无饱和性和方向性) 晶体结构:(每个金属原子的电子云分布基本 上是球对称的) 同一种金属原子—等径圆球 堆积—密堆积 →面心立方,六角密堆,体心立方 晶体特征:稳定,密度大,硬度高, 熔点高,导电,传热,延展性。 密度泛函理论: 结合能1 ∼ 5eV/原子 2.4 分子晶体、金属及氢键晶体 53 四 氢键晶体 弱键,解释某些“精细”的结合特性时起重要 作用 结合力:氢键(氢原子同时和其它两个原子 键合形成) 键的特点来源于氢原子的特性: ¾价电子电离能高(13.6eV)(Na原子5.14eV) ¾只有一个价电子,形成一个共价键, 不能构成典型的共价晶体 ¾离子实很小 2.4 分子晶体、金属及氢键晶体 54 氢原子的价电子与其它原子形成共价键 后,电子云分布靠近共价键一边,另一边 氢原子核暴露在外,可以通过库仑力作用 与另一个电负性较大的原子相结合。 2.4 分子晶体、金属及氢键晶体

五其它结合类型品体 C60分子品体: 混合型品体: 接 健(层出 整个层 24分于西体。金4天氢做品体 西北家机实税人大行24会于西体4远能通体 碳钠米管: 神奇的碳纳米管 高机城度 于幅100倍,16重 隆青保喷技 通向月球的天梯 北家航空就天大香 25原子的真电根和昌株随合机障 硬钠米管基鹰身材料 2.5原子的真电性和晶体结合规律 瓷质林费合持有奖烧泽 来能力的)角度定性 去一个电子所必需的能量 中性原子-()+正离子 亲和能: 所整个电子成为离子 中性原子++负离子
10 55 五 其它结合类型晶体 混合型晶体: 石墨:三个价电子与近邻形成三个共价 键(层状)一个价电子在整个层自由运动, 金属键(导电)层与层靠瞬时偶极矩互作用 而结合(疏松) 2.4 分子晶体、金属及氢键晶体 56 C60分子晶体: 1985年,H. W. Kroto, R. E. Smalley和 B. Curl采用 激光加热石墨蒸发并在甲苯中形成碳的团簇,质谱分析 意外地发现由 60个碳原子组成的封闭的足球型C60分 子。由于其奇特的结构和性质,引发了富勒烯研究热 潮。 1996年三人同获诺贝尔化学奖。 C60的发现者之一 R.E.Smalley教授 2.4 分子晶体、金属及氢键晶体 57 1991年,日本电气公司的饭岛澄男(S. Iijima)发现碳纳 米管(多壁管),1993年又发现单壁碳纳米管。 碳纳米管 的质量是钢的六分之一,强度是钢的100倍。 Iijima教授 碳纳米管: 2.4 分子晶体、金属及氢键晶体 58 神奇的碳纳米管 通向月球的天梯 高机械强度: 大于钢100倍,1/6重 量 高长径比: 103数量级 高比表面: 400- 500m2/g 具有金属性或半导体 性,化学性质不活泼 2.4 分子晶体、金属及氢键晶体 59 碳纳米管基隐身材料 碳 纳 米 管 金属、半导体性、可调 超强超轻 中空结构(0.4-10nm) 手性结构 优良的微波吸收材料 结构强化材料 2.4 分子晶体、金属及氢键晶体 60 2.5 原子的负电性和晶体结合规律 从原子的负电性(对价电子束缚能力的)角度定性 说明晶体结合的有关规律。 一 原子的负电性 电离能:使原子失去一个电子所必需的能量 中性原子– (–e)→正离子 亲和能:一个原子获得一个电子成为负离子 所放出的能量。 中性原子 + (–e)→负离子 2.5 原子的负电性和晶体结合规律