
第七章 能量带 如果晶体是金属,绝缘体,牛导体,那么是由什么来决定的? 固体的能带结构 自由电子模型一忽略电子与离子和其它电子的相互作用 失效: ⑧金属,牛导体和绝缘体之间的差别 ⑧正的Hal系数值. ⑧磁-输运. 能带结构一考虑相互作用 独立电子图象一在运动,数运方程里处理独立的载流子 1
1 第七章 能量带 如果晶体是 金属, 绝缘体,半导体,那么是由什么来决定的? 固体的能带结构 自由电子模型 – 忽略电子与离子和 其它电子的相互作用. 失效 : ⊗ 金属, 半导体 和 绝缘体之间的差别. ⊗ 正的Hall系数值. ⊗ 磁-输运 . ⊗ . 能带结构 – 考虑相互作用 独立电子图象 – 在运动,数运方程里处理独立的载流子

晶体是金属,绝缘体,或牛导体是由什么决定的? 固体的能带结构 空态 空态 空态 满态 满态 满态 导电带 价带满/ 导电带空 部分占满 E。>keT 金属 牢导体 绝缘体一 传导电子是有效的 在高温或掺杂下,传导电 没有传导电子 子是有效的 2
2 晶体是金属, 绝缘体, 或 半导体 是由什么决定的? 固体的能带结构 满 态 空 态 导电 带 部分占满 满 态 空 态 Eg 价 带 满 / Eg>kBT 空 态 满 态 Eg 金属 半导体 绝缘体 传导电子是有效的 在高温或掺杂下,传导电 子是有效的 没有传导电子 E
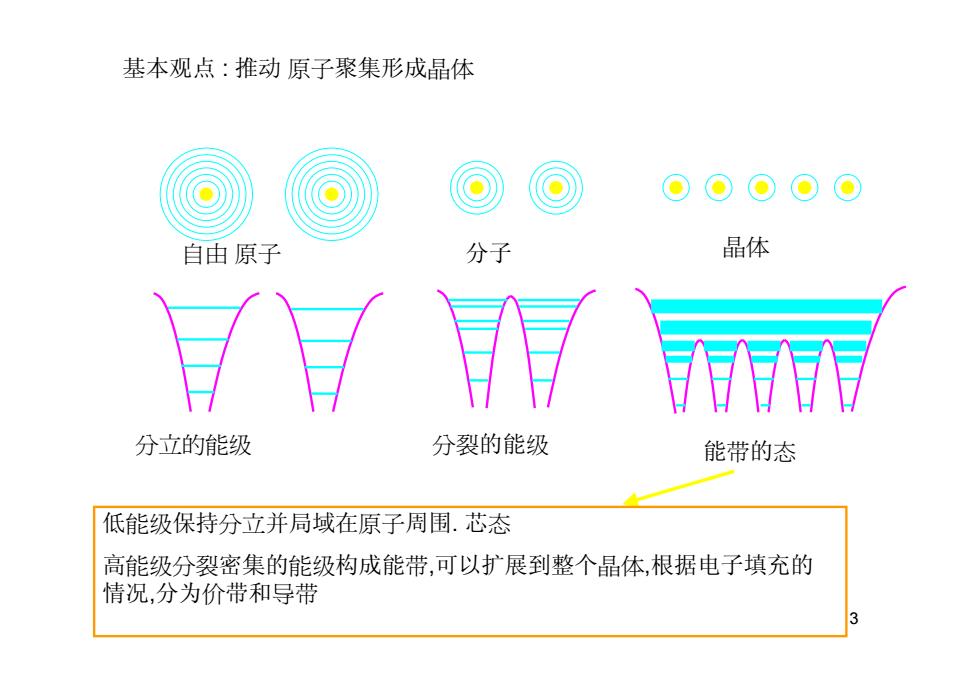
基本观点:推动原子聚集形成晶体 自由原子 分子 晶体 而 分立的能级 分裂的能级 能带的态 低能级保持分立并局域在原子周围.芯态 高能级分裂密集的能级构成能带,可以扩展到整个晶体,根据电子填充的 情况,分为价带和导带
3 基本观点 : 推动 原子聚集形成晶体 自由 原子 分子 晶体 分立的能级 分裂的能级 能带的态 低能级保持分立并局域在原子周围. 芯态 高能级分裂密集的能级构成能带,可以扩展到整个晶体,根据电子填充的 情况,分为价带和导带
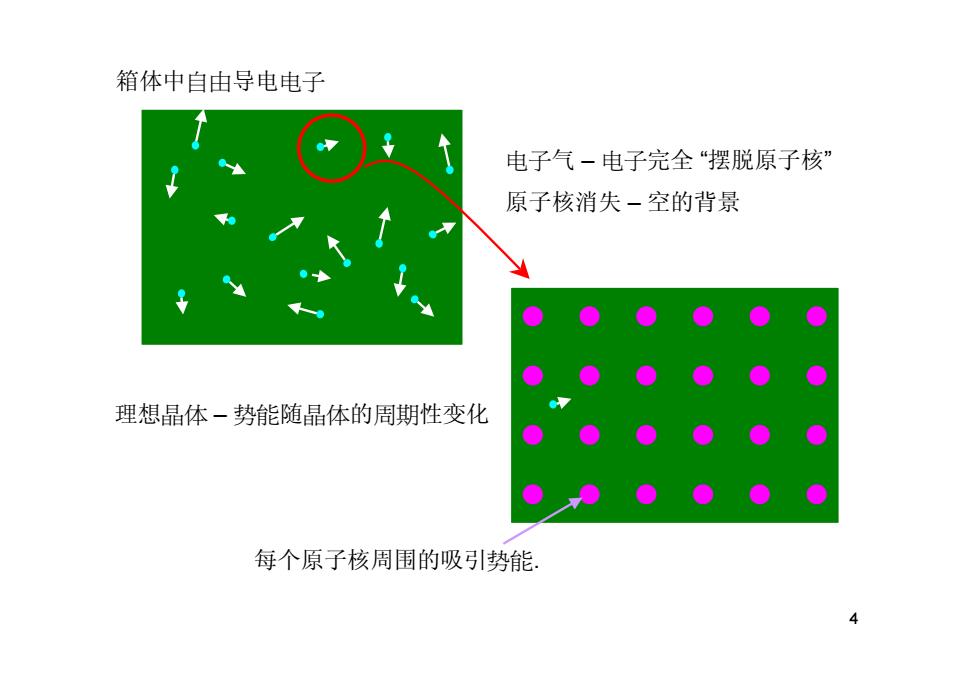
箱体中自由导电电子 电子气-电子完全“摆脱原子核” 原子核消失一空的背景 理想晶体一势能随晶体的周期性变化 每个原子核周围的吸引势能。 4
4 箱体中自由导电电子 电子气 – 电子完全 “摆脱原子核” 原子核消失 – 空的背景 理想晶体 – 势能随晶体的周期性变化 每个原子核周围的吸引势能

近自由电子模型 -把离子的周期势加到自由电子 带电子 两个结果: (1)布洛赫定理-是薛定谔方程的形式解 Ψk()=uk(①exp依●i) 布洛赫波函数 平面波函数 由于周期势形成的周期函数 uk(T)=uk(I+T)=uk(T+uja+u2a2+u3a3) 实空间中的格矢 自由和束缚混合特征 自由:拓展到整个晶体 束缚:受离子芯相互作用的调制 (2)能隙-能带状态的开放间隙 5
5 近自由 电子模型 - 把离子的周期势加到自由 电子 带电子 两个结果 : (1) 布洛赫定理 –是薛定谔方程 的形式解 ψ )r( u )r( exp( ki r) k k r r r r = • 平面波函数 u )r( u r( )T u r( u a u a u a ) k k k 1 1 2 2 3 3 r r r r r r r = + = + + + 由于周期势形成的周期函数 实空间中的格矢 布洛赫波 函数 自由 和 束缚混合特征 自由 : 拓展到整个晶体 束缚 : 受离子芯相互作用的调制 (2) 能隙 – 能带状态的开放间隙
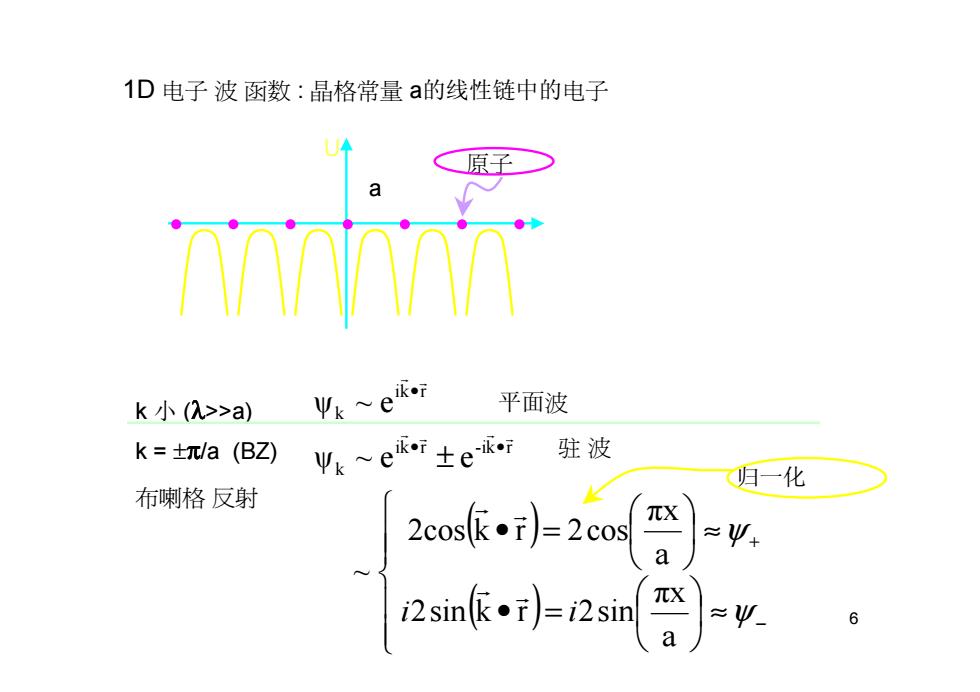
1D电子波函数:晶格常量a的线性链中的电子 原平 rmnnr k小(2>>a) Ψk~eiki 平面波 k=±元/a(BZ) Vk~e&f±ekr 驻波 归一化 布喇格反射 2cos()=2cos X ≈ a i2sin)=12sin ≈ 6
6 1D 电子 波 函数 : 晶格常量 a的线性链中的电子 k 小 (λ>>a) ki r k ψ ~ e r r • k = ±π/a (BZ) ( ) ( ) a πx 2sin k r 2sin a πx 2cos k r 2cos ~ ψ ~ e e ki r -ik r k ≈ • = ≈ • = ± −+ • • ψ ψ i i r r r r r r r r 平面波 驻 波 U x a 原子 布喇格 反射 归一化
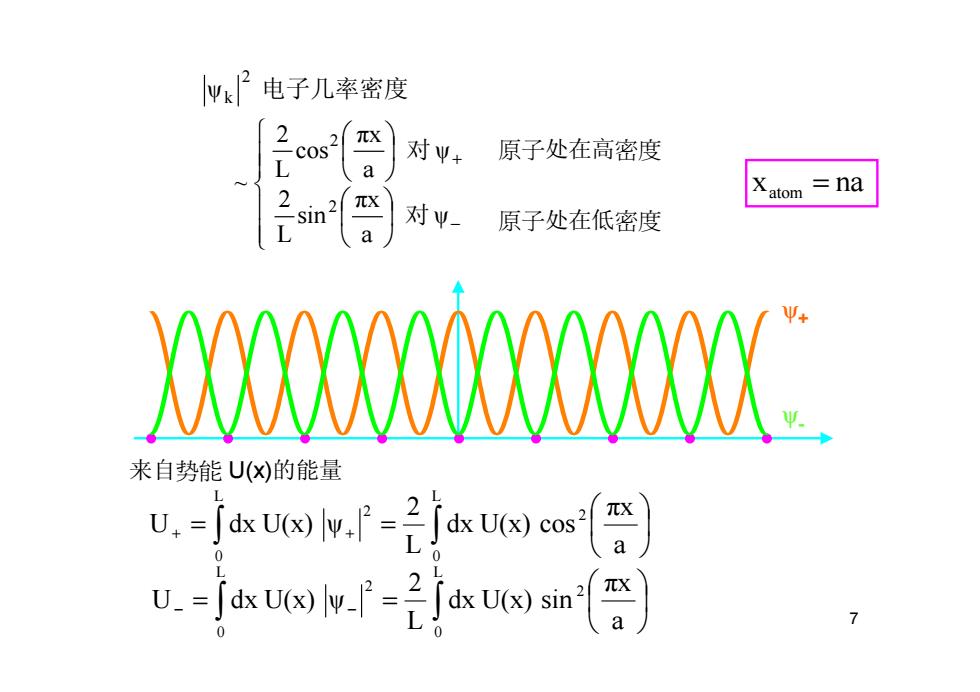
电子几率密度 2 元X coS 原子处在高密度 L a 对业+ 2 atom =na 元X sin 对Ψ_ L 原子处在低密度 a w0M0d 来自势能U()的能量 u,-uepf-2jeas U-jw-2jsm 元X a 7
7 ψ a πx sin L 2 ψ a πx cos L 2 ~ ψ 2 2 2 k −+ 对对 电子几率密度 原子处在高密度 原子处在低密度 来自势能 U(x)的能量 a πx dx U(x) sin L2 U dx U(x) ψ a πx dx U(x) cos L2 U dx U(x) ψ L 0 2 L 0 2 L 0 2 L 0 2 ∫ ∫ ∫ ∫ = = = = − − + + 几率 密度 x ψ+ ψ- x na atom =
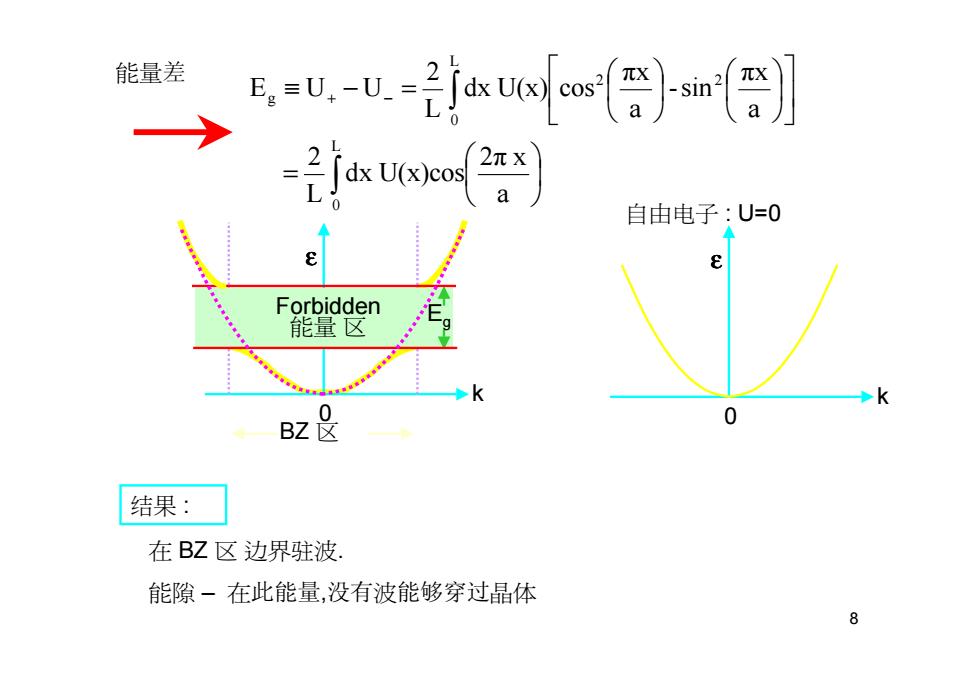
能量差 -uc oo-in) 2X 自由电子:U=0 Forbidden 能量区 0 BZ 0 结果: 在BZ区边界驻波. 能隙一在此能量,没有波能够穿过晶体 8
8 a 2π x dx U(x)cos L2 a πx -sin a πx dx U(x) cos L2 E U U L 0 L 0 2 2 g ∫ ∫ = ≡ + − − = 能量差 k ε BZ 区 Eg Forbidden 能量 区 0 自由电子 : U=0 k ε 0 在 BZ 区 边界驻波. 能隙 – 在此能量,没有波能够穿过晶体 结果 :
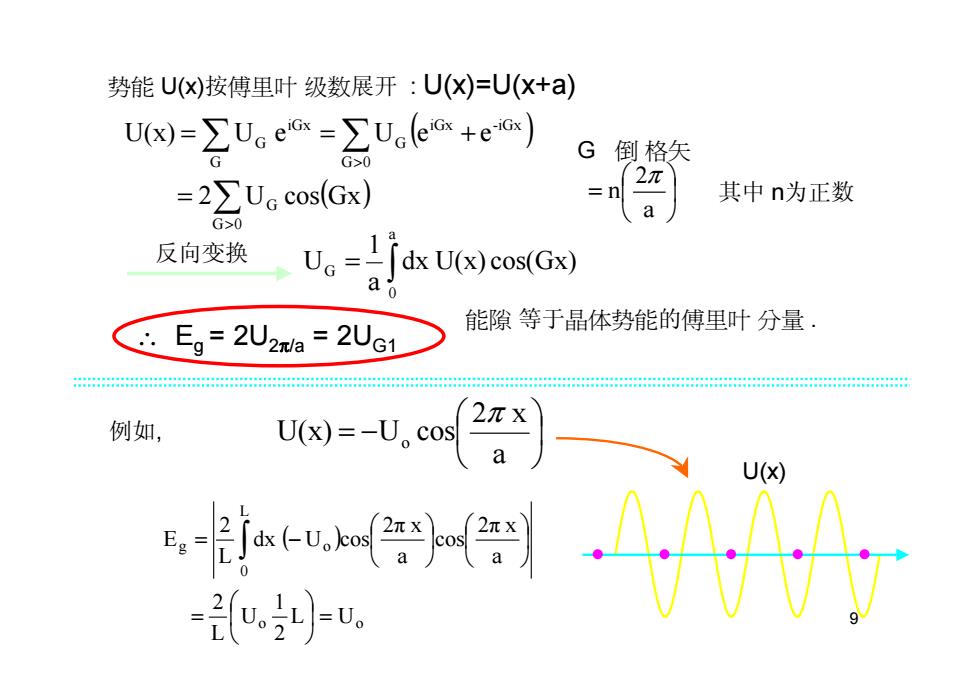
势能U(x)按傅里叶级数展开:U(X)=(X+a) U(x)=∑U=∑Ua(eos+eor) G G>0 G倒格矢 2π =2∑Uccos(Gx) =nl 其中n为正数 G>0 a 反向变换 dx U(x)cos(Gx) Eg=2U2/a =2 2UG1 能隙等于晶体势能的傅里叶分量· 222222a22828a2a2 例如, U(x)-U,c0s a 之小 U(X) -(v.iL)-v
9 ∫ = a 0 G dx U(x) cos(Gx) a 1 反向变换 U ∴ Eg = 2U2π/a = 2UG1 能隙 等于晶体势能的傅里叶 分量 . 例如, ( ) o o L 0 g o L U 2 1 U L 2 a 2π x cos a 2π x dx U cos L 2 E = = = − ∫ x U(x) = − a 2 x U(x) U cos o π 势能 U(x)按傅里叶 级数展开 : U(x)=U(x+a) ( ) ∑ ( ) ∑ ∑ > > = = = + G 0 G G 0 iGx -iGx G G iGx G 2 U cos Gx U(x) U e U e e G : 倒 格矢 其中 n为正数 = a2 n π
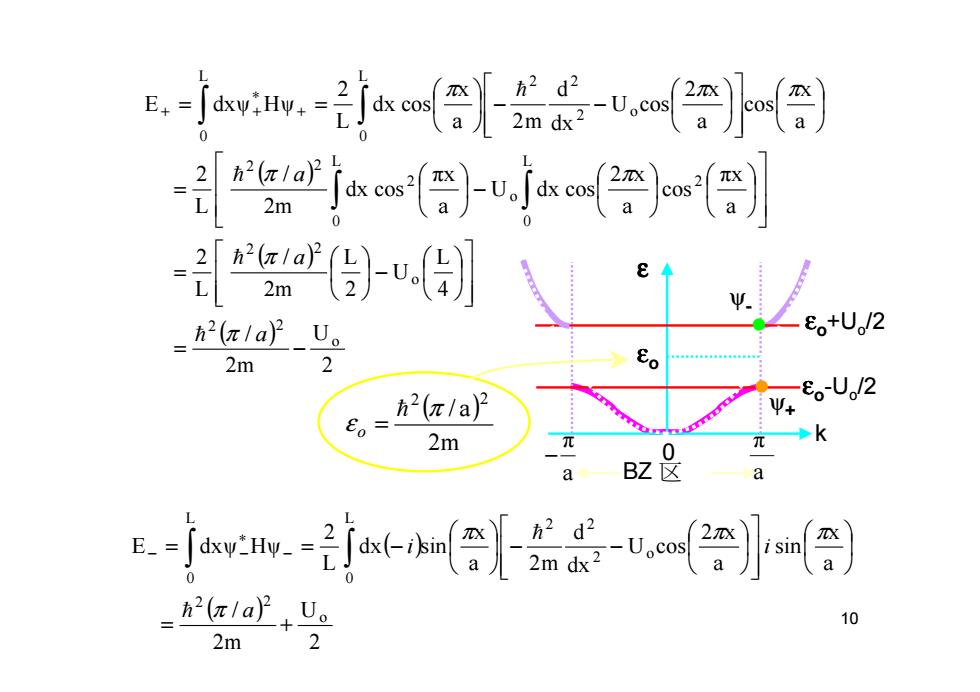
,-jww益-uog) o)-v.a) h2(π1a2U。 Eo+U/2 2m 2 h2(π/a2 。-UJ2 Ψ+ 2m 0 a BZ -jww水-tame( 2πa2+U 10 2m
10 ( ) ( ) ( ) 2 U 2m / 4 L U 2 L 2m / L 2 a πx cos a 2 x U dx cos a πx dx cos 2m / L 2 a x cos a 2 x U cos dx d a 2 m x dx cos L 2 E dxψ Hψ o 2 2 o 2 2 L 0 2 o L 0 2 2 2 L 0 L 0 o 2 2 2 = − − = − = − − = = ∫ ∫ ∫ ∫ + ∗ + + a a a π π π π π π π h h h h ( ) ( ) 2 U 2m / a x sin a 2 x U cos dx d a 2 m x dx sin L 2 E dxψ Hψ o 2 2 L 0 L 0 o 2 2 2 = + − − = = − ∫ ∫ − ∗ − − a i i π π π π h h k ε BZ 区 0 a π a π − ψ + ψ- ε o ε o+U o/2 ε o-U o/2 ( ) 2 m a/ 2 2 π ε h o =