第四章声子!晶格振动 格子是非刚性的.原子可以在平衡点附件运动. 基元原子 振动 当波在固鄰传播时,存在个纵向和两个横向极化(偏 +2 +4 a S+2 S+3 S+4 s-3 S- s-1 S+1S+2
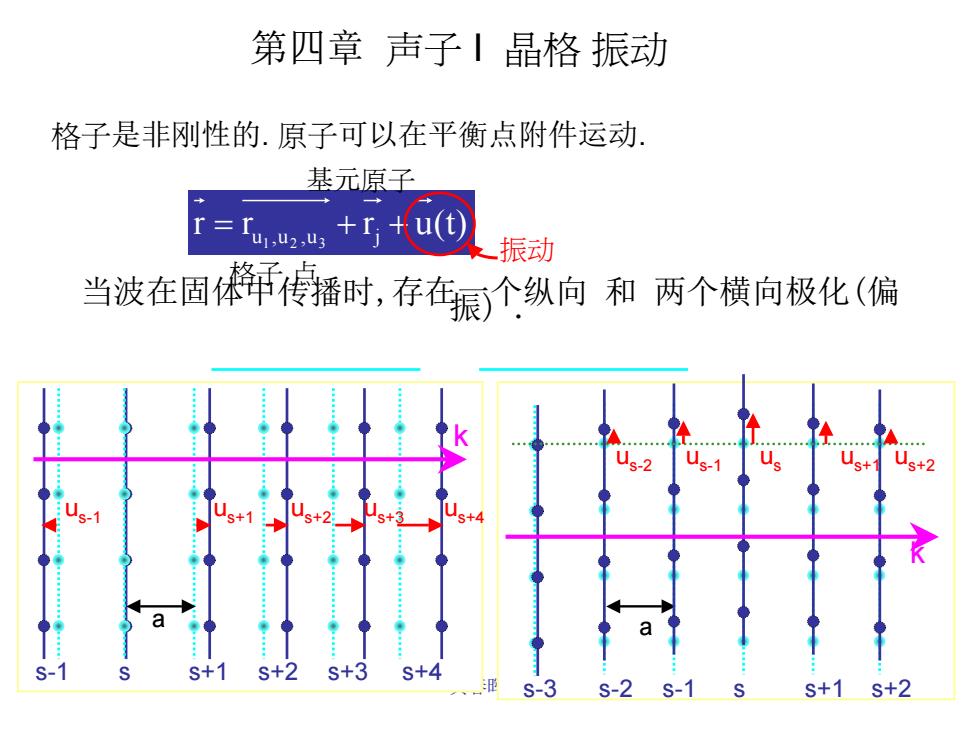
黄春晖 编 第四章 声子 I 晶格 振动 格子是非刚性的. 原子可以在平衡点附件运动. r r r u(t) u ,u ,u j 1 2 3 = + + 振动 格子 点 基元原子 当波在固体中传播时,存在一个纵向 振) . 和 两个横向极化(偏 s-3 s-2 s-1 s s+1 s+2 a s-1 s s+1 s+2 s+3 s+4 a us-2 us-1 us+2 us us+1 us-1 us+1 us+2 us+3 us+4 k k

1D晶格振动 M Us-2 Us-1 F Us Fp us+1 F=FR +FL=C(us+I-u)+C(us-1-u,) dg=Cu4+u,-2u,) dt2 组藕合,线性的,二阶微分方程 ©通常情况下如果M和C不同,很难求解, ©方法:试探解(很好猜测) u,()=Aexp[kx。-ot】 这里X=sa 黄春晖编
黄春晖 编 1D 晶格振动 MMM M us-2 us-1 us us+1 C C C C C FL FR C(u u 2u ) dt d u M F F F C(u u ) C(u u ) 2 s 1 s 1 s s 2 s R L s 1 s s 1 s = + − = + = − + − + − + − ☻ 一组藕合,线性的,二阶微分方程. ☻ 通常情况下如果 M 和 C不同,很难求解. ☻ 方法 : 试探解 (很好猜测) 这里 x u (t) Aexp[ (kx t)] s=sa s = i s −ω
M(-2)Aeiksei=C(Aeik(s+Aeik(s-D-2Aksa le-iot -Mo2=Clea +e-ika-2) =C2(cos(ka)-1) 02= -co:(kw-)-2sn) M 4C ka 0三 sin M 2 色散关系 1.0 08 当k= 4C a :最大 0.4 M 0.2 处在第一 BZ边界 0.0 -1.5 -1.0 050.00.5 1.01.5 k[(2π/a)m]
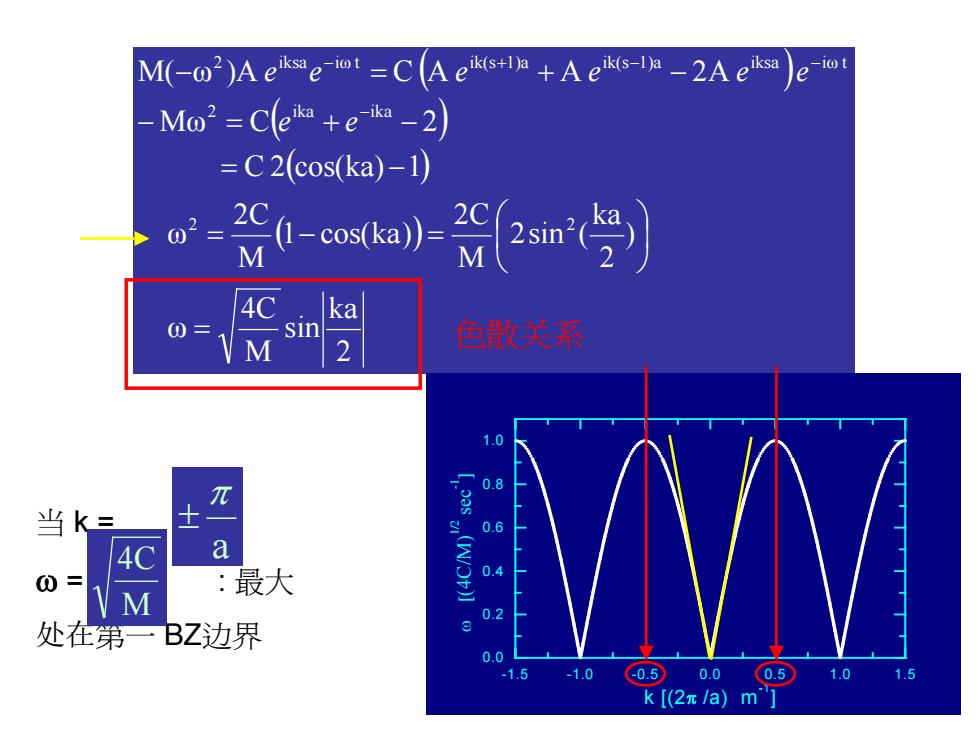
黄春晖 编 ( ) ( ) ( ) ( ) 2 ka sin M 4C ω ) 2ka 2sin ( M2C 1 cos(ka) M2C ω C 2 cos(ka) 1 Mω C 2 M( ω )A C A A 2A 2 2 2 ika ika 2 iksa iω t ik(s 1)a ik(s 1)a iksa iω t = = − = = − − = + − − = + − − − + − − e e e e e e e e 色散关系 当 k = ω = : 最大 处在第一 BZ边界 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 0.0 0.2 0.4 0.6 0.8 1.0 ω [(4C/M)1/2 sec -1 ] k [(2π /a) m-1] a π± M 4C
对于小的k(ka<<1) 长波极限 4C ka Ca Ca M 2 M M/a vk 连续弹性波极限 色散:O≠Vk 相 速度Vp 波速度是什么? 速度 相速度 k do 群速度 三 g dk Vi (k) 在介质中能量传播速度
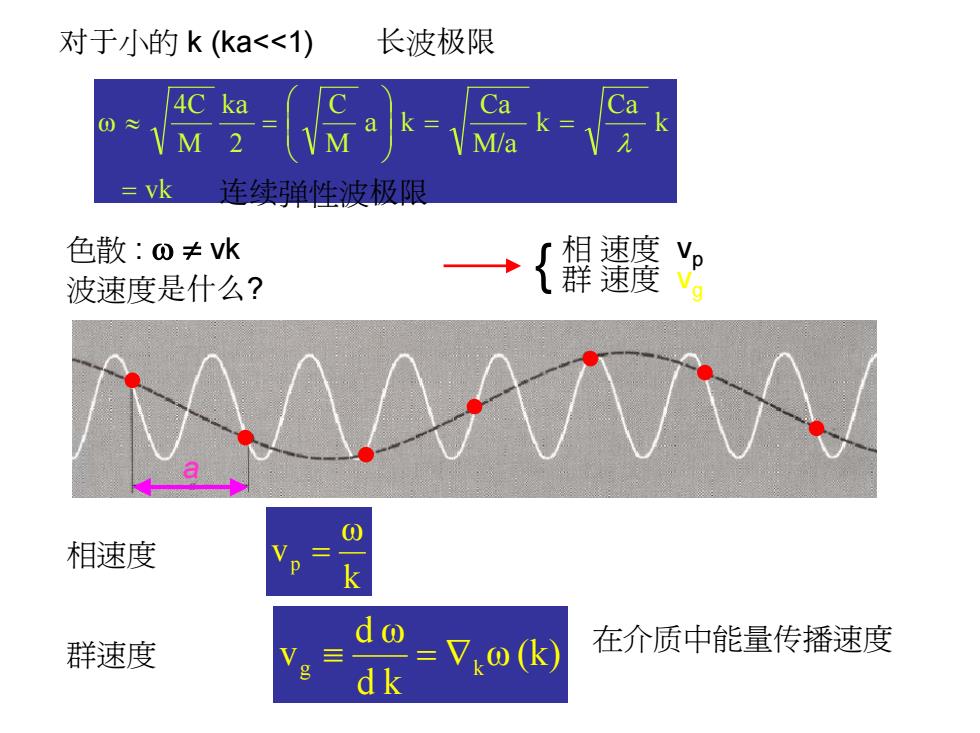
黄春晖 编 对于小的 k (ka<<1) 长波极限 vk k Ca k M/a Ca a k M C 2 ka M 4C ω = = = ≈ = λ 连续弹性波极限 色散 : ω ≠ vk 波速度是什么? 相 速度 vp 群 速度 vg { a k ω v 相速度 p = ω (k) d k d ω vg ≡ = ∇k 在介质中能量传播速度 群速度

时间增加 群速度 do g dk .=V@(k) 相速度 时间增加 黄春晖编
黄春晖 编 (a) (b) (c) (d) (d) (e) (f) (g) 时 间 增 加 群速度 ω (k) d k d ω v g ≡ = ∇ k 相速度 k ω v 时 p = 间 增 加
相速度 群速度 0 ,√4C/M sin(ka /2) dw d sin(ka /2) =√4C/M k k dk dk a 4C sin(ka /2) a 4C ka cos( 2 M ka/2 M 2 sin(ka/2) =V V2 =v,|cos(ka/2) ka/2 当k= Vg0群速度消失!V。=(2/m a (k处在第一边界) 正格子 na 倒格子 G 2π m Bragg条件 a BZ边界 2 a
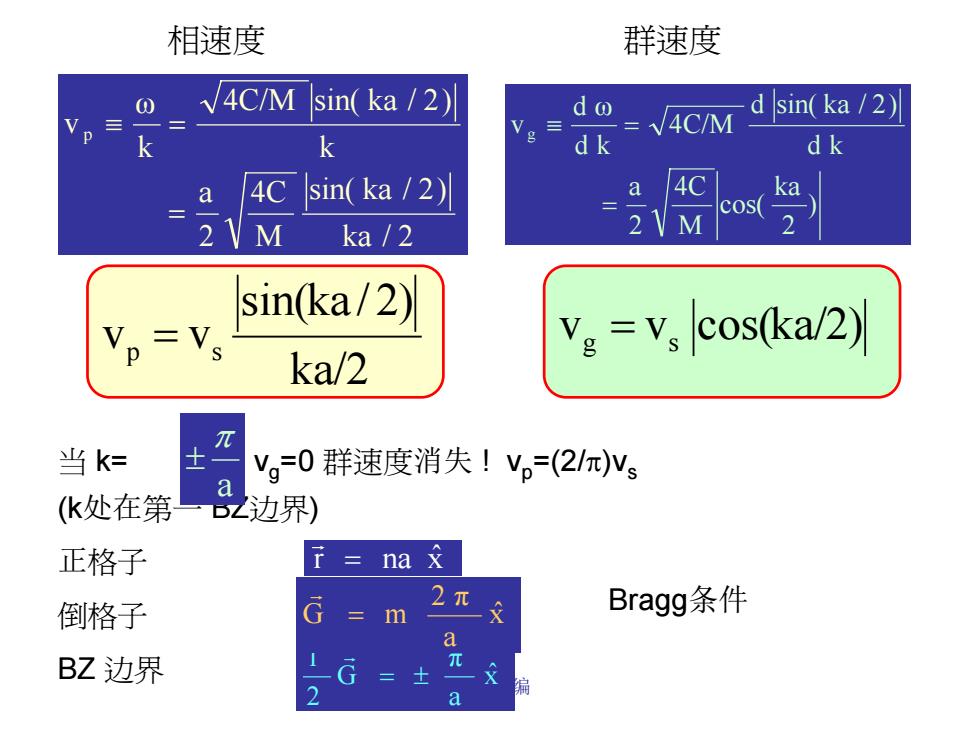
黄春晖 编 相速度 群速度 ka / 2 sin( ka / 2) M 4C 2 a k 4C/M sin( ka / 2) k ω v p = ≡ = ) 2ka cos( M4C 2a d k d sin( ka / 2) 4C/M d k d ω vg = ≡ = ka/2 sin(ka / 2) v v p = s v v cos(ka/2) g = s 当 k= , vg=0 群速度消失 ! vp=(2/π)vs (k处在第一 BZ边界) 正格子 倒格子 BZ 边界 r = na x ˆ r Bragg条件 x ˆ a π G 2 1 = ± r x ˆ a 2 π G = m r a π±
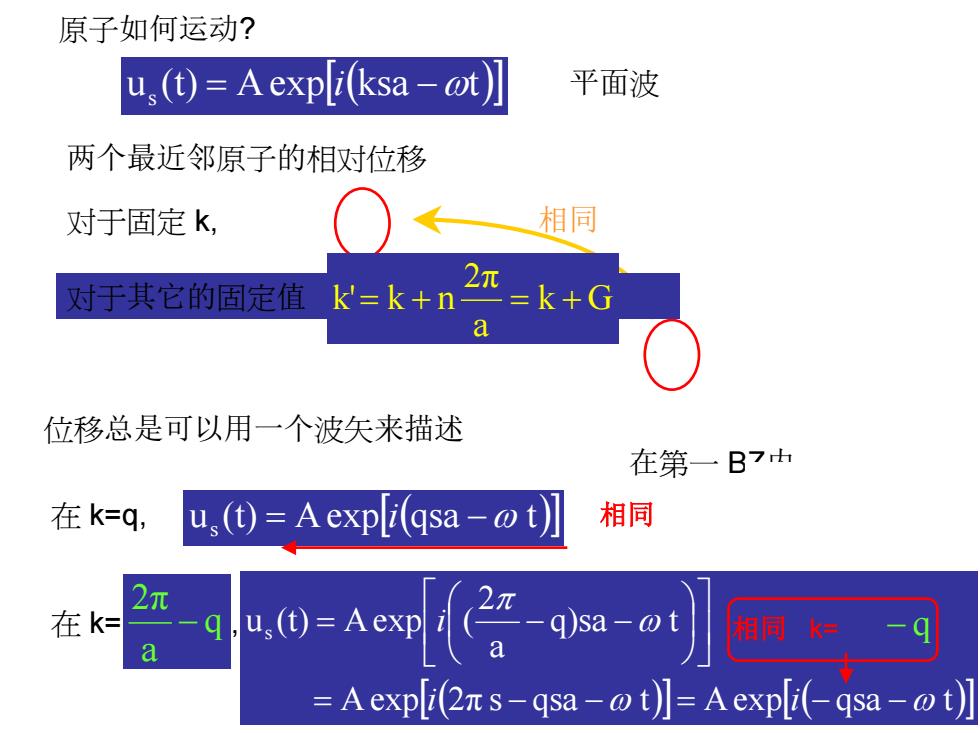
原子如何运动? u,(t)Aexpli(ksa-@t) 平面波 两个最近邻原子的相对位移 对于固定k, 相同 2 对于其它的固定值 k'=k+n 2=k+G a 位移总是可以用一个波矢来描述 在第一B7h 在k=q, us(t)=Aexpli(qsa-@t) 相同 2元 在k= Q)sa-@t 相同k三 a =Aexp[i(2元s-qsa-ot】=Aexp[(-9sa-otJ
黄春晖 编 原子如何运动? u (t) Aexp[ (ksa t)] s = i −ω 平面波 两个最近邻原子的相对位移 在 k=q, 在 k= , ika s s 1 u u = e + i(k n2π /a)a ika in2π ika s s 1 u u = e = e e = e + + 相同 位移总是可以用一个波矢来描述 在第一 BZ内. 对于其它的固定值 k G a 2π k'= k + n = + u (t) Aexp[ (qsa t)] s = i −ω Aexp[ ] ( ) 2π s qsa t Aexp[ ] ( ) qsa t q)sa t a 2 u (t) Aexp ( s ω ω ω π = − − = − − = − − i i q i a 2π − 相同 k= q a 2π + 相同 k= − q 对于固定 k

=4a3 =49/7 入A 入=4a 入1=4a, 2元 k1 4a 2a 4a 3π2元 k2= 2a 2a 4a 5π 2元 k3= 2a 2a 4a 1元 人4三 7, k= 2a 黄春晖编
黄春晖 编 λ=4a λ=4a/3 λ=4a/7 2a π 4a 2 π λ 4 a , k 1 = 1 = = 2a π a 2 π 2a 3 π , k 34a λ 2 = 2 = = − 2a π a 2 π 2a 5 π , k 54a λ 3 = 3 = = + 2a π a 2 π 2 2a 7 π , k 74a λ 4 4 − = = =
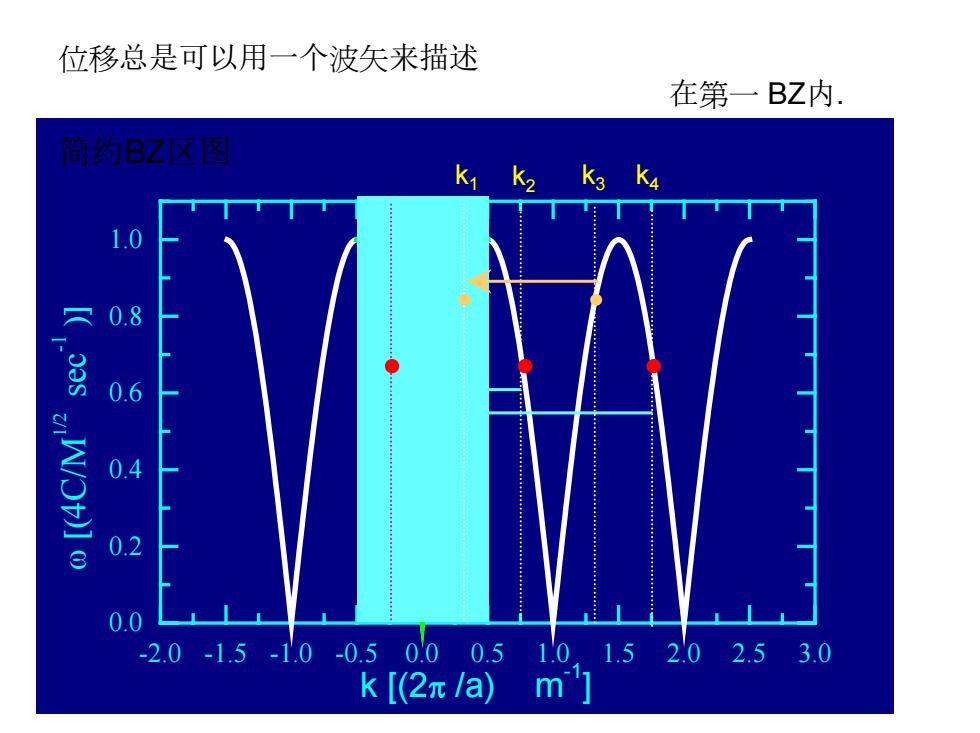
位移总是可以用一个波矢来描述 在第一BZ内. 简约BZ×图 K1 K2 K3 k4 1.0 只 0.8 0.6 0.4 0.2 0.0 -2.0.-1.5-1.0-0.50.00.510,1.52.02.53.0 k[2π/a)m'1
黄春晖 编 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 0.0 0.2 0.4 0.6 0.8 1.0 ω [(4C/M1/ 2 sec -1 )] k [(2π /a) m-1] 位移总是可以用一个波矢来描述 在第一 BZ内. k1 k3 k4 简约BZ区图 k2

考虑到k范围遍及整个倒空间,O(K)的表达式是周期性 所有信息都在第一Brillouin zone:余下的都是具有2π/a周期性 的重复-即,O(K和o(k+G)是相同的,这里G是任意倒格矢 2元 =nx a 倒空间周期性 事实上,波矢为k的原子运动和波矢为k+G的原子运动是一致的 所有独立的振动用BZ内的k来描述. 黄春晖编
黄春晖 编 考虑到k范围遍及整个倒空间, ω(k)的表达式是周期性. 所有 信息都在第一 Brillouin zone : 余下的都是具有2π/a周期性 的重复– 即, ω(k)和 ω(k+G) 是相同的,这里G是任意倒格矢 a 2π G = n × 倒空间周期性 事实上, 波矢 为 的原子运动和波矢为 的原子运动是一致的. 所有独立的振动用 BZ 内的 k 来描述 . r k r k G r r +