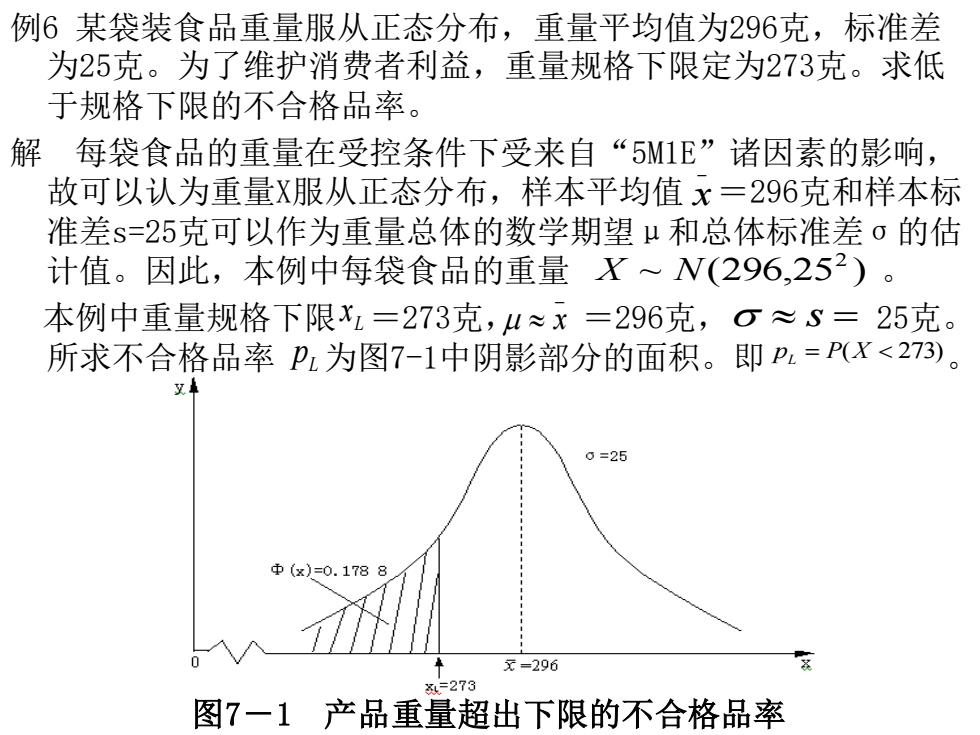
例6某袋装食品重量服从正态分布，重量平均值为296克，标准差 为25克。为了维护消费者利益，重量规格下限定为273克。求低 于规格下限的不合格品率。 解每袋食品的重量在受控条件下受来自“5M1E”诸因素的影响， 故可以认为重量X服从正态分布，样本平均值x=296克和样本标 准差s=25克可以作为重量总体的数学期望μ和总体标准差σ的估 计值。因此，本例中每袋食品的重量X~N(296,252)。 本例中重量规格下限xL=273克，u≈x=296克，O≈=25克。 所求不合格品率p为图7-1中阴影部分的面积。即P.=(x<273)。 0=25 中(x)=0.1788 元=296 =273 图7-1 产品重量超出下限的不合格品率例6 某袋装食品重量服从正态分布，重量平均值为296克，标准差 为25克。为了维护消费者利益，重量规格下限定为273克。求低 于规格下限的不合格品率。 解 每袋食品的重量在受控条件下受来自“5M1E”诸因素的影响， 故可以认为重量X服从正态分布，样本平均值 ＝296克和样本标 准差s=25克可以作为重量总体的数学期望μ和总体标准差σ的估 计值。因此，本例中每袋食品的重量 。 本例中重量规格下限 ＝273克， ＝296克， 25克。 所求不合格品率 为图7-1中阴影部分的面积。即 。 _ x ~ (296,25 ) 2 X N L x _   x   s = L p p = P(X  273) L 图7－1 产品重量超出下限的不合格品率