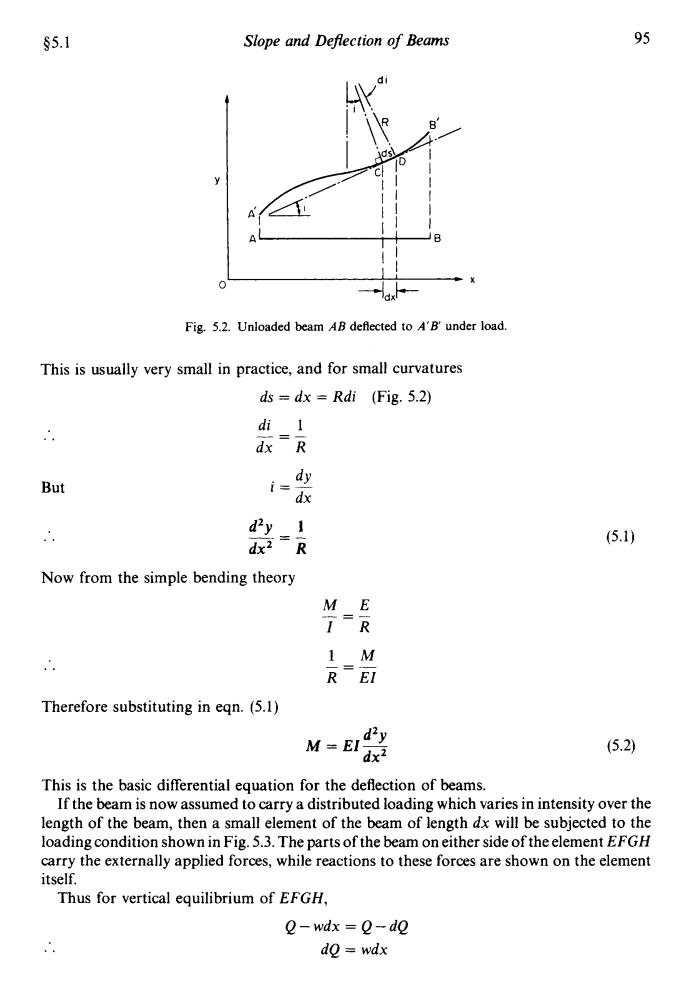
§5.1 Slope and Deflection of Beams 95 A O Fig.5.2.Unloaded beam AB deflected to A'B'under load. This is usually very small in practice,and for small curvatures ds =dx Rdi (Fig.5.2) di 1 dy But i= dx d2y I (5.1) dx2R Now from the simple bending theory 1 M R= El Therefore substituting in eqn.(5.1) M=EI d2y dx? (52) This is the basic differential equation for the deflection of beams. If the beam is now assumed to carry a distributed loading which varies in intensity over the length of the beam,then a small element of the beam of length dx will be subjected to the loading condition shown in Fig.5.3.The parts of the beam on either side of the element EFGH carry the externally applied forces,while reactions to these forces are shown on the element itself. Thus for vertical equilibrium of EFGH, o-wax =o-do do=wdx$5.1 Slope and Defection of Beams 95 Fig. 5.2. Unloaded beam AB deflected to A’B’ under load. This is usually very small in practice, and for small curvatures ds = dx = Rdi (Fig. 5.2) di 1 dx R -- -- But .. . dY I=- dx d2y 1 dx2 R -=- Now from the simple bending theory ME IR -- -- Therefore substituting in eqn. (5.1) M=EI- d2Y dx2 This is the basic differential equation for the deflection of beams. If the beam is now assumed to carry a distributed loading which varies in intensity over the length of the beam, then a small element of the beam of length dx will be subjected to the loading condition shown in Fig. 5.3. The parts of the beam on either side of the element EFGH carry the externally applied forces, while reactions to these forces are shown on the element itself. Thus for vertical equilibrium of EFGH, .. Q-wdx = Q-dQ dQ = wdx