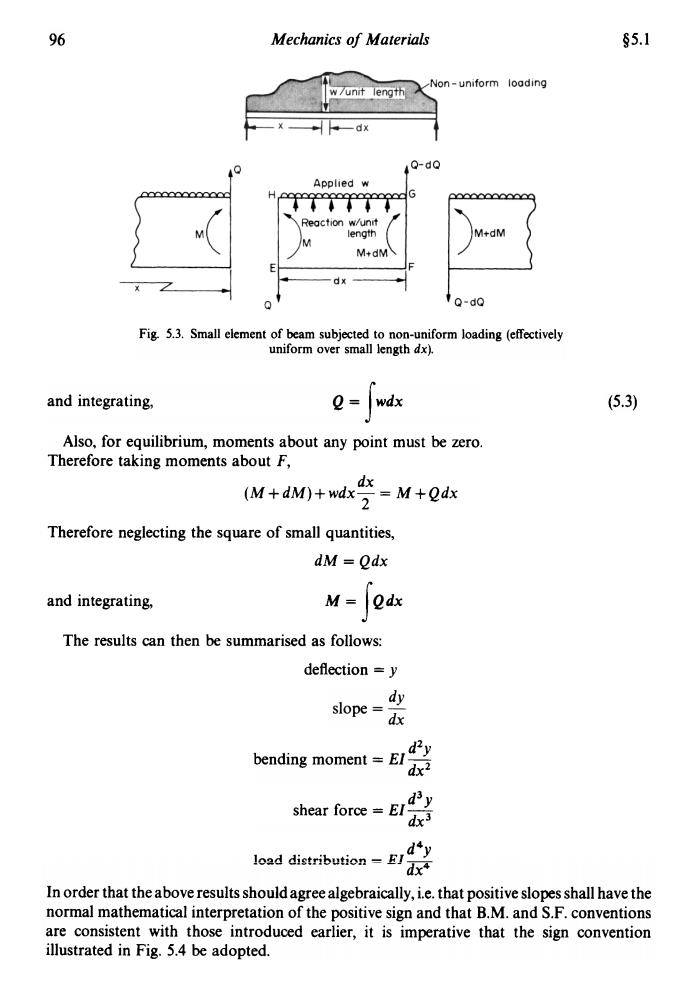
96 Mechanics of Materials s5.1 Non-uniform loading w/unit length 一d 4Q-do Applied w Seeeeeec Reaction w/unit length M+dM M+dM Q-do Fig.5.3.Small element of beam subjected to non-uniform loading (effectively uniform over small length dx). and integrating, 2=wdx (5.3) Also,for equilibrium,moments about any point must be zero. Therefore taking moments about F, M+dM0+wdx?=M+2d成 Therefore neglecting the square of small quantities, dM =Odx and integrating, M=Qdx The results can then be summarised as follows: deflection =y dy slope= dx bending moment =EI dy dx shear force =EI d3y dx load distribution =EI dx In order that the above results should agree algebraically,i.e.that positive slopes shall have the normal mathematical interpretation of the positive sign and that B.M.and S.F.conventions are consistent with those introduced earlier,it is imperative that the sign convention illustrated in Fig.5.4 be adopted.96 Mechanics of Materials §5.1 Fig. 5.3. Small element of beam subjected to non-uniform loading (effectively uniform over small length dx). (5.3) and integrating, Q = f wdx Also, for equilibrium, moments about any point must be zero. Therefore taking moments about F, dx (M+dM)+wdxT = M+Qdx Therefore neglecting the square of small quantities, dM = Qdx and integrating, M = f Qdx The results can then be summarised as follows: deflection = y d2y bending moment = El ~ d3 shear force = El -JJ d4 In~ti tii~trihlltinn = 1':1 ~ .~-- -.~...~-..~.. --dx4 In order that the above results should agree algebraically, i.e. that positive slopes shall have the normal mathematical interpretation of the positive sign and that B.M. and S.F. conventions are consistent with those introduced earlier, it is imperative that the sign convention illustrated in Fig. 5.4 be adopted