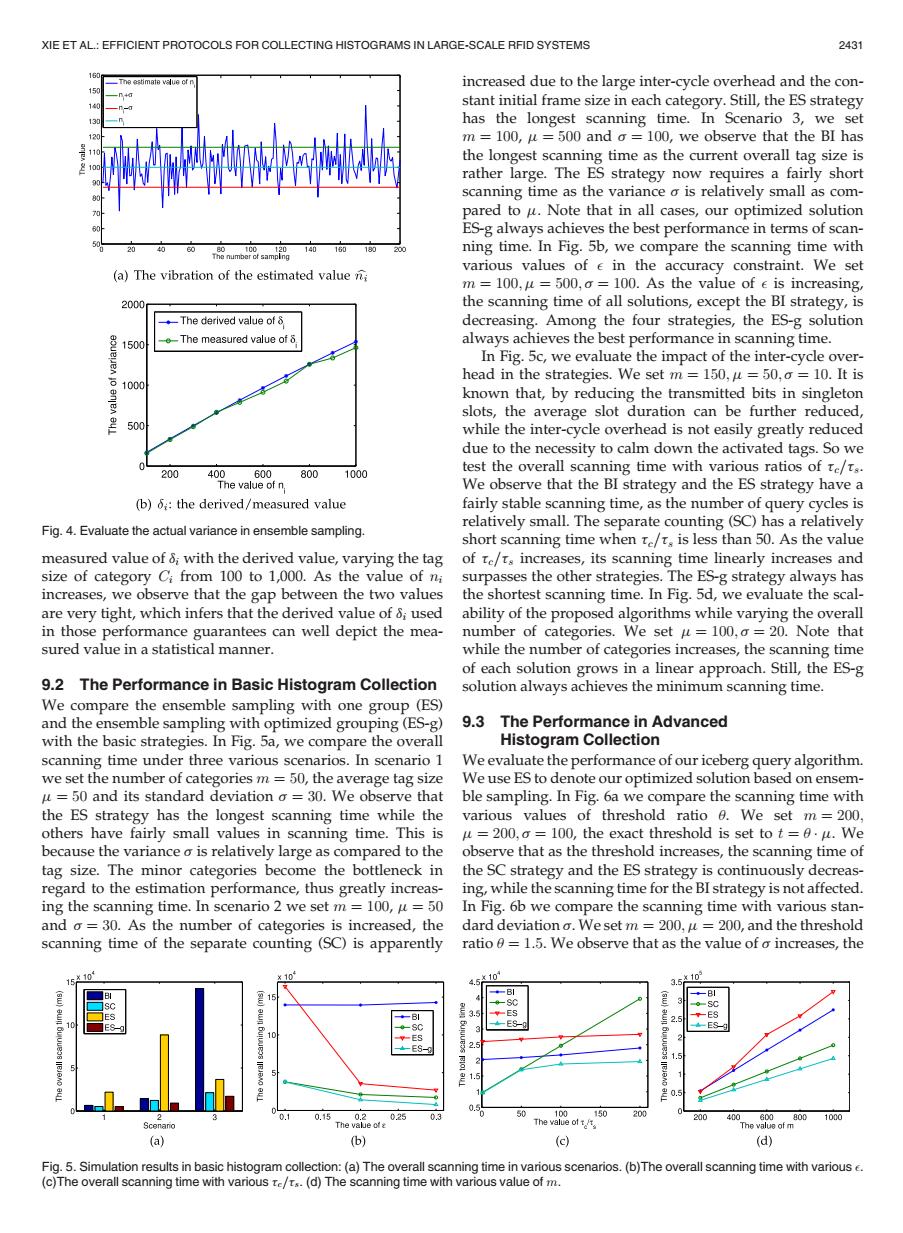
XIE ET AL.:EFFICIENT PROTOCOLS FOR COLLECTING HISTOGRAMS IN LARGE-SCALE RFID SYSTEMS 2431 increased due to the large inter-cycle overhead and the con- stant initial frame size in each category.Still,the ES strategy has the longest scanning time.In Scenario 3,we set 城 m =100,u=500 and o=100,we observe that the BI has the longest scanning time as the current overall tag size is rather large.The ES strategy now requires a fairly short scanning time as the variance o is relatively small as com- pared to u.Note that in all cases,our optimized solution ES-g always achieves the best performance in terms of scan- 60 140 16017 ning time.In Fig.5b,we compare the scanning time with various values of e in the accuracy constraint.We set (a)The vibration of the estimated value m =100,u=500,o=100.As the value of e is increasing 2000 the scanning time of all solutions,except the BI strategy,is -The derived value of 8 decreasing.Among the four strategies,the ES-g solution 岁1500 The measured value of 8. always achieves the best performance in scanning time. In Fig.5c,we evaluate the impact of the inter-cycle over- head in the strategies.We set m =150,u=50,o =10.It is 1000 known that,by reducing the transmitted bits in singleton slots,the average slot duration can be further reduced, 500 while the inter-cycle overhead is not easily greatly reduced due to the necessity to calm down the activated tags.So we 0 200 400 600 800 1000 test the overall scanning time with various ratios of re/rs. The value of n, We observe that the BI strategy and the ES strategy have a (b);:the derived/measured value fairly stable scanning time,as the number of query cycles is Fig.4.Evaluate the actual variance in ensemble sampling. relatively small.The separate counting(SC)has a relatively short scanning time when re/t,is less than 50.As the value measured value of &with the derived value,varying the tag of re/rs increases,its scanning time linearly increases and size of category Ci from 100 to 1,000.As the value of ni surpasses the other strategies.The ES-g strategy always has increases,we observe that the gap between the two values the shortest scanning time.In Fig.5d,we evaluate the scal- are very tight,which infers that the derived value of 8;used ability of the proposed algorithms while varying the overall in those performance guarantees can well depict the mea- number of categories.We set u=100,20.Note that sured value in a statistical manner while the number of categories increases,the scanning time of each solution grows in a linear approach.Still,the ES-g 9.2 The Performance in Basic Histogram Collection solution always achieves the minimum scanning time. We compare the ensemble sampling with one group(ES) and the ensemble sampling with optimized grouping(ES-g) 9.3 The Performance in Advanced with the basic strategies.In Fig.5a,we compare the overall Histogram Collection scanning time under three various scenarios.In scenario 1 We evaluate the performance of our iceberg query algorithm. we set the number of categories m =50,the average tag size We use ES to denote our optimized solution based on ensem- u=50 and its standard deviation o =30.We observe that ble sampling.In Fig.6a we compare the scanning time with the ES strategy has the longest scanning time while the various values of threshold ratio 0.We set m=200 others have fairly small values in scanning time.This is u=200,o=100,the exact threshold is set to t=0.u.We because the variance o is relatively large as compared to the observe that as the threshold increases,the scanning time of tag size.The minor categories become the bottleneck in the SC strategy and the ES strategy is continuously decreas- regard to the estimation performance,thus greatly increas-ing,while the scanning time for the BI strategy is not affected. ing the scanning time.In scenario 2 we set m 100,u=50 In Fig.6b we compare the scanning time with various stan- and o=30.As the number of categories is increased,the dard deviation o.We set m=200,u=200,and the threshold scanning time of the separate counting (SC)is apparently ratio =1.5.We observe that as the value of o increases,the ×10 10 x10 g10 -Bl -S0 .1 0.15 0.2 025 50 150 200 a00 400 G00 1000 Scenario The The vae of (a) (b) (c) (d) Fig.5.Simulation results in basic histogram collection:(a)The overall scanning time in various scenarios.(b)The overall scanning time with various e. (c)The overall scanning time with various re/r..(d)The scanning time with various value of m.measured value of di with the derived value, varying the tag size of category Ci from 100 to 1,000. As the value of ni increases, we observe that the gap between the two values are very tight, which infers that the derived value of di used in those performance guarantees can well depict the mea￾sured value in a statistical manner. 9.2 The Performance in Basic Histogram Collection We compare the ensemble sampling with one group (ES) and the ensemble sampling with optimized grouping (ES-g) with the basic strategies. In Fig. 5a, we compare the overall scanning time under three various scenarios. In scenario 1 we set the number of categories m ¼ 50, the average tag size m ¼ 50 and its standard deviation s ¼ 30. We observe that the ES strategy has the longest scanning time while the others have fairly small values in scanning time. This is because the variance s is relatively large as compared to the tag size. The minor categories become the bottleneck in regard to the estimation performance, thus greatly increas￾ing the scanning time. In scenario 2 we set m ¼ 100, m ¼ 50 and s ¼ 30. As the number of categories is increased, the scanning time of the separate counting (SC) is apparently increased due to the large inter-cycle overhead and the con￾stant initial frame size in each category. Still, the ES strategy has the longest scanning time. In Scenario 3, we set m ¼ 100, m ¼ 500 and s ¼ 100, we observe that the BI has the longest scanning time as the current overall tag size is rather large. The ES strategy now requires a fairly short scanning time as the variance s is relatively small as com￾pared to m. Note that in all cases, our optimized solution ES-g always achieves the best performance in terms of scan￾ning time. In Fig. 5b, we compare the scanning time with various values of in the accuracy constraint. We set m ¼ 100;m ¼ 500; s ¼ 100. As the value of is increasing, the scanning time of all solutions, except the BI strategy, is decreasing. Among the four strategies, the ES-g solution always achieves the best performance in scanning time. In Fig. 5c, we evaluate the impact of the inter-cycle over￾head in the strategies. We set m ¼ 150;m ¼ 50; s ¼ 10. It is known that, by reducing the transmitted bits in singleton slots, the average slot duration can be further reduced, while the inter-cycle overhead is not easily greatly reduced due to the necessity to calm down the activated tags. So we test the overall scanning time with various ratios of tc=ts. We observe that the BI strategy and the ES strategy have a fairly stable scanning time, as the number of query cycles is relatively small. The separate counting (SC) has a relatively short scanning time when tc=ts is less than 50. As the value of tc=ts increases, its scanning time linearly increases and surpasses the other strategies. The ES-g strategy always has the shortest scanning time. In Fig. 5d, we evaluate the scal￾ability of the proposed algorithms while varying the overall number of categories. We set m ¼ 100; s ¼ 20. Note that while the number of categories increases, the scanning time of each solution grows in a linear approach. Still, the ES-g solution always achieves the minimum scanning time. 9.3 The Performance in Advanced Histogram Collection We evaluate the performance of our iceberg query algorithm. We use ES to denote our optimized solution based on ensem￾ble sampling. In Fig. 6a we compare the scanning time with various values of threshold ratio u. We set m ¼ 200; m ¼ 200; s ¼ 100, the exact threshold is set to t ¼ u  m. We observe that as the threshold increases, the scanning time of the SC strategy and the ES strategy is continuously decreas￾ing, while the scanning time for the BI strategy is not affected. In Fig. 6b we compare the scanning time with various stan￾dard deviation s. We set m ¼ 200;m ¼ 200, and the threshold ratio u ¼ 1:5. We observe that as the value of s increases, the Fig. 4. Evaluate the actual variance in ensemble sampling. Fig. 5. Simulation results in basic histogram collection: (a) The overall scanning time in various scenarios. (b)The overall scanning time with various . (c)The overall scanning time with various tc=ts. (d) The scanning time with various value of m. XIE ET AL.: EFFICIENT PROTOCOLS FOR COLLECTING HISTOGRAMS IN LARGE-SCALE RFID SYSTEMS 2431