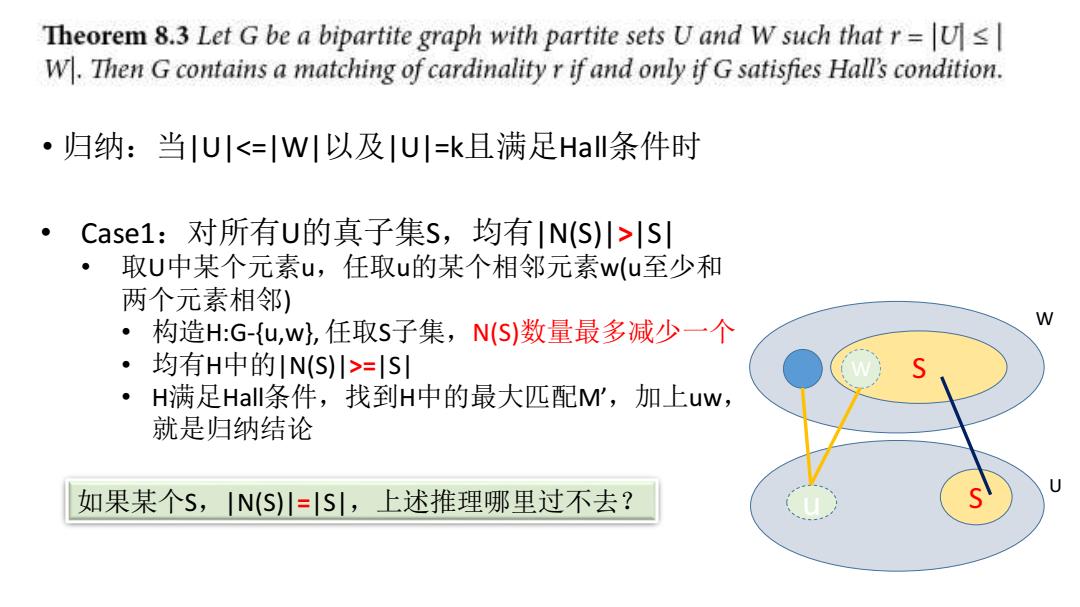
Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. ·归纳：当U川<=WI以及U川=k且满足Hall条件时 case1:对所有U的真子集S,均有IN(s)川>lS ·取U中某个元素u,任取u的某个相邻元素w(u至少和 两个元素相邻) ·构造H:G-{u,w,任取S子集，N(S)数量最多减少一个 W ·均有H中的IN(S)川>=|S H满足Hal条件，找到H中的最大匹配M',加上uw, 就是归纳结论 如果某个S,N(S)川=S,上述推理哪里过不去？U W S u S W • 归纳：当|U|<=|W|以及|U|=k且满足Hall条件时 • Case1：对所有U的真子集S，均有|N(S)|>|S| • 取U中某个元素u，任取u的某个相邻元素w(u至少和 两个元素相邻) • 构造H:G-{u,w}, 任取S子集，N(S)数量最多减少一个 • 均有H中的|N(S)|>=|S| • H满足Hall条件，找到H中的最大匹配M’，加上uw， 就是归纳结论 如果某个S，|N(S)|=|S|，上述推理哪里过不去？