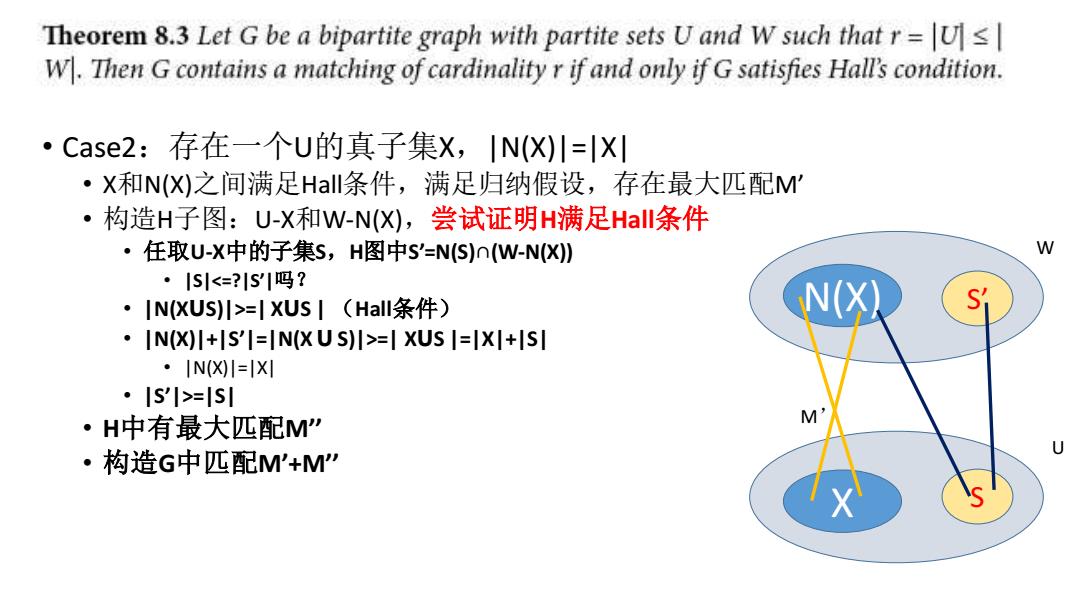
Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. ·Case2:存在一个U的真子集X,IN(X)川=X ·X和N()之间满足Hal条件，满足归纳假设，存在最大匹配M' ·构造H子图：U-X和W-N(X),尝试证明H满足HaII条件 ·任取U-X中的子集s,H图中s'=NS)n(W-N(X) W ·1S1<=?1S1吗？ ·IN(XUs)l>=|XUsI(Hall条件) N() Si .IN(X)I+S'I=IN(XUS)I>=I XUS I=IXI+ISI ·IN(X)=X ·IsI>=lsl ·H中有最大匹配M” U ·构造G中匹配M'+M• Case2：存在一个U的真子集X，|N(X)|=|X| • X和N(X)之间满足Hall条件，满足归纳假设，存在最大匹配M’ • 构造H子图：U-X和W-N(X)，尝试证明H满足Hall条件 • 任取U-X中的子集S，H图中S’=N(S)∩(W-N(X)) • |S|<=?|S’|吗？ • |N(XꓴS)|>=| XꓴS | （Hall条件） • |N(X)|+|S’|=|N(X ꓴ S)|>=| XꓴS |=|X|+|S| • |N(X)|=|X| • |S’|>=|S| • H中有最大匹配M’’ • 构造G中匹配M’+M’’ U W X N(X) S S’ M’