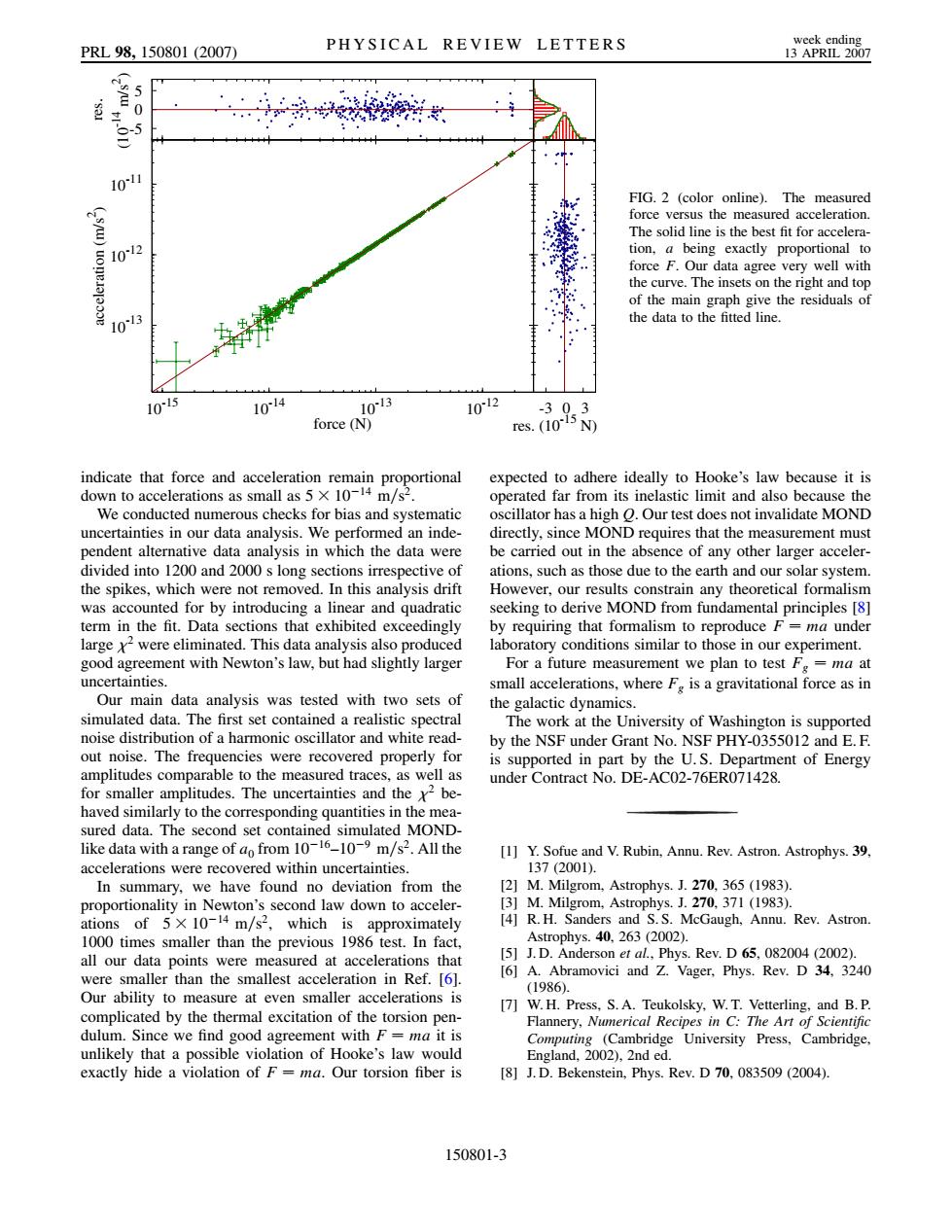
PHYSICAL REVIEW LETTERS week ending PRL98,150801(2007) 13 APRIL 2007 5 0 。-5 101 FIG.2 (color online).The measured force versus the measured acceleration. The solid line is the best fit for accelera- 1012 tion,a being exactly proportional to force F.Our data agree very well with the curve.The insets on the right and top of the main graph give the residuals of 1013 the data to the fitted line. 105 10l4 1013 10~12 -30.3 force (N) res.(1015N indicate that force and acceleration remain proportional expected to adhere ideally to Hooke's law because it is down to accelerations as small as 5 x 10-14 m/s2. operated far from its inelastic limit and also because the We conducted numerous checks for bias and systematic oscillator has a high O.Our test does not invalidate MOND uncertainties in our data analysis.We performed an inde- directly,since MOND requires that the measurement must pendent alternative data analysis in which the data were be carried out in the absence of any other larger acceler- divided into 1200 and 2000 s long sections irrespective of ations,such as those due to the earth and our solar system. the spikes,which were not removed.In this analysis drift However,our results constrain any theoretical formalism was accounted for by introducing a linear and quadratic seeking to derive MOND from fundamental principles [8] term in the fit.Data sections that exhibited exceedingly by requiring that formalism to reproduce F=ma under large xwere eliminated.This data analysis also produced laboratory conditions similar to those in our experiment. good agreement with Newton's law,but had slightly larger For a future measurement we plan to test F=ma at uncertainties. small accelerations,where F is a gravitational force as in Our main data analysis was tested with two sets of the galactic dynamics. simulated data.The first set contained a realistic spectral The work at the University of Washington is supported noise distribution of a harmonic oscillator and white read- by the NSF under Grant No.NSF PHY-0355012 and E.F. out noise.The frequencies were recovered properly for is supported in part by the U.S.Department of Energy amplitudes comparable to the measured traces,as well as under Contract No.DE-AC02-76ER071428. for smaller amplitudes.The uncertainties and the x2 be- haved similarly to the corresponding quantities in the mea- sured data.The second set contained simulated MOND- like data with a range of do from 10-16-10-9 m/s2.All the [1]Y.Sofue and V.Rubin,Annu.Rev.Astron.Astrophys.39 accelerations were recovered within uncertainties 137(2001). In summary,we have found no deviation from the [2]M.Milgrom,Astrophys.J.270,365(1983). proportionality in Newton's second law down to acceler- [3]M.Milgrom,Astrophys.J.270,371 (1983). ations of 5x 10-14 m/s2,which is approximately [4]R.H.Sanders and S.S.McGaugh,Annu.Rev.Astron. 1000 times smaller than the previous 1986 test.In fact, Astrophys..40,263(2002). all our data points were measured at accelerations that [51 J.D.Anderson et al.,Phys.Rev.D 65,082004 (2002). were smaller than the smallest acceleration in Ref.[6]. [6]A.Abramovici and Z.Vager,Phys.Rev.D 34,3240 (1986). Our ability to measure at even smaller accelerations is [7]W.H.Press,S.A.Teukolsky,W.T.Vetterling,and B.P. complicated by the thermal excitation of the torsion pen- Flannery,Numerical Recipes in C:The Art of Scientific dulum.Since we find good agreement with F=ma it is Computing (Cambridge University Press,Cambridge, unlikely that a possible violation of Hooke's law would England,2002),2nd ed. exactly hide a violation of F=ma.Our torsion fiber is [8]J.D.Bekenstein,Phys.Rev.D 70,083509(2004). 150801-3indicate that force and acceleration remain proportional down to accelerations as small as 5 1014 m=s2. We conducted numerous checks for bias and systematic uncertainties in our data analysis. We performed an inde￾pendent alternative data analysis in which the data were divided into 1200 and 2000 s long sections irrespective of the spikes, which were not removed. In this analysis drift was accounted for by introducing a linear and quadratic term in the fit. Data sections that exhibited exceedingly large 2 were eliminated. This data analysis also produced good agreement with Newton’s law, but had slightly larger uncertainties. Our main data analysis was tested with two sets of simulated data. The first set contained a realistic spectral noise distribution of a harmonic oscillator and white read￾out noise. The frequencies were recovered properly for amplitudes comparable to the measured traces, as well as for smaller amplitudes. The uncertainties and the 2 be￾haved similarly to the corresponding quantities in the mea￾sured data. The second set contained simulated MOND￾like data with a range of a0 from 1016–109 m=s2. All the accelerations were recovered within uncertainties. In summary, we have found no deviation from the proportionality in Newton’s second law down to acceler￾ations of 5 1014 m=s2, which is approximately 1000 times smaller than the previous 1986 test. In fact, all our data points were measured at accelerations that were smaller than the smallest acceleration in Ref. [6]. Our ability to measure at even smaller accelerations is complicated by the thermal excitation of the torsion pen￾dulum. Since we find good agreement with F
ma it is unlikely that a possible violation of Hooke’s law would exactly hide a violation of F
ma. Our torsion fiber is expected to adhere ideally to Hooke’s law because it is operated far from its inelastic limit and also because the oscillator has a high Q. Our test does not invalidate MOND directly, since MOND requires that the measurement must be carried out in the absence of any other larger acceler￾ations, such as those due to the earth and our solar system. However, our results constrain any theoretical formalism seeking to derive MOND from fundamental principles [8] by requiring that formalism to reproduce F
ma under laboratory conditions similar to those in our experiment. For a future measurement we plan to test Fg
ma at small accelerations, where Fg is a gravitational force as in the galactic dynamics. The work at the University of Washington is supported by the NSF under Grant No. NSF PHY-0355012 and E. F. is supported in part by the U. S. Department of Energy under Contract No. DE-AC02-76ER071428. [1] Y. Sofue and V. Rubin, Annu. Rev. Astron. Astrophys. 39, 137 (2001). [2] M. Milgrom, Astrophys. J. 270, 365 (1983). [3] M. Milgrom, Astrophys. J. 270, 371 (1983). [4] R. H. Sanders and S. S. McGaugh, Annu. Rev. Astron. Astrophys. 40, 263 (2002). [5] J. D. Anderson et al., Phys. Rev. D 65, 082004 (2002). [6] A. Abramovici and Z. Vager, Phys. Rev. D 34, 3240 (1986). [7] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing (Cambridge University Press, Cambridge, England, 2002), 2nd ed. [8] J. D. Bekenstein, Phys. Rev. D 70, 083509 (2004). 10-13 10-12 10-11 10-15 10-14 10-13 10-12 acceleration (m/s2 ) force (N) -5 0 5 res. (10-14 m/s2 ) -3 0 3 res. (10-15 N) FIG. 2 (color online). The measured force versus the measured acceleration. The solid line is the best fit for accelera￾tion, a being exactly proportional to force F. Our data agree very well with the curve. The insets on the right and top of the main graph give the residuals of the data to the fitted line. PRL 98, 150801 (2007) PHYSICAL REVIEW LETTERS week ending 13 APRIL 2007 150801-3