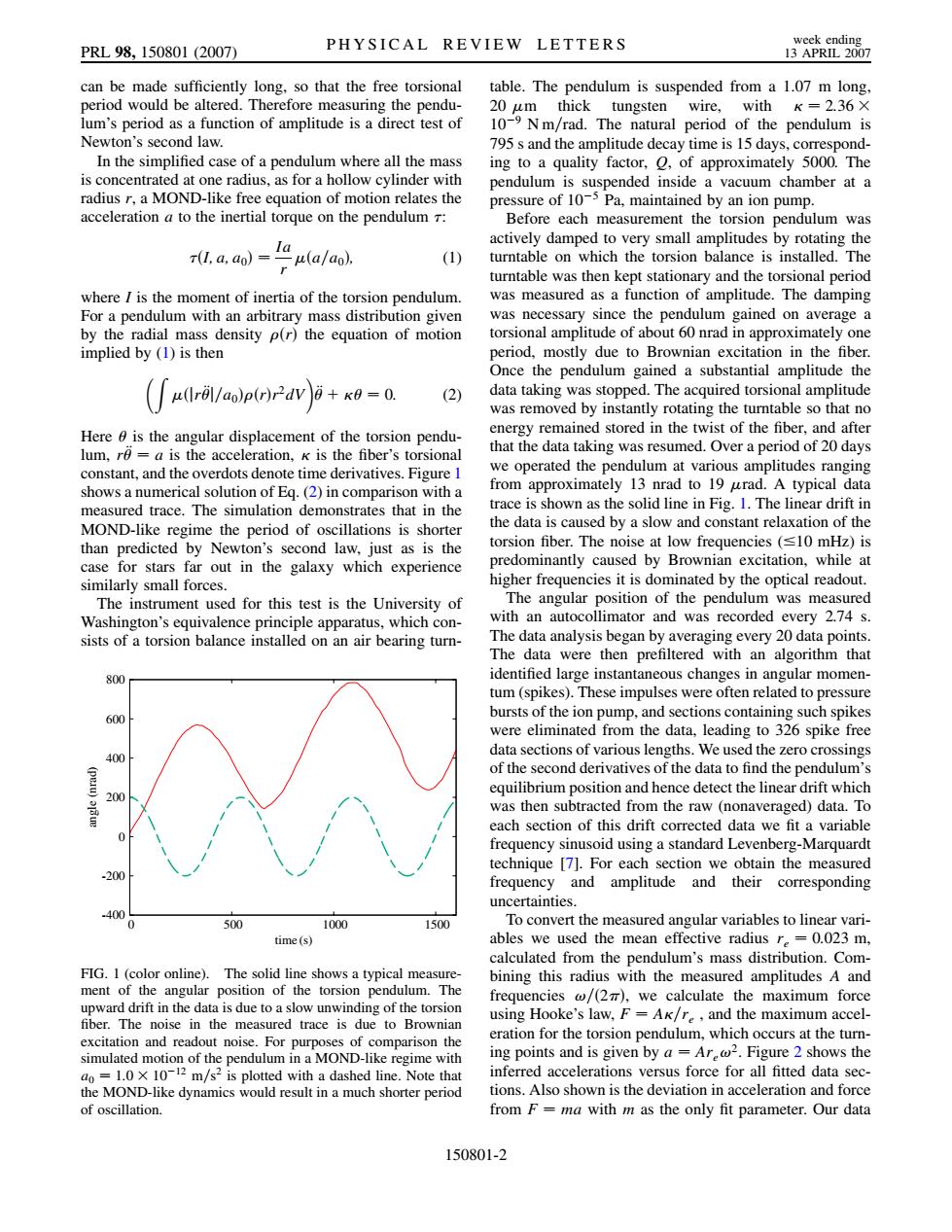
week ending PRL98,150801(2007) PHYSICAL REVIEW LETTERS 13 APRIL 2007 can be made sufficiently long,so that the free torsional table.The pendulum is suspended from a 1.07 m long, period would be altered.Therefore measuring the pendu- 20 um thick tungsten wire,with k=2.36X lum's period as a function of amplitude is a direct test of 10-9 Nm/rad.The natural period of the pendulum is Newton's second law. 795 s and the amplitude decay time is 15 days,correspond- In the simplified case of a pendulum where all the mass ing to a quality factor,of approximately 5000.The is concentrated at one radius,as for a hollow cylinder with pendulum is suspended inside a vacuum chamber at a radius r,a MOND-like free equation of motion relates the pressure of 10-5 Pa,maintained by an ion pump. acceleration a to the inertial torque on the pendulum r: Before each measurement the torsion pendulum was actively damped to very small amplitudes by rotating the T(I,a,do)=la u(alao). (1) turntable on which the torsion balance is installed.The turntable was then kept stationary and the torsional period where is the moment of inertia of the torsion pendulum. was measured as a function of amplitude.The damping For a pendulum with an arbitrary mass distribution given was necessary since the pendulum gained on average a by the radial mass density p(r)the equation of motion torsional amplitude of about 60 nrad in approximately one implied by (1)is then period,mostly due to Brownian excitation in the fiber. Once the pendulum gained a substantial amplitude the (u(ril/ao)p(dv)o+xo-0. (2) data taking was stopped.The acquired torsional amplitude was removed by instantly rotating the turntable so that no Here 6 is the angular displacement of the torsion pendu- energy remained stored in the twist of the fiber,and after lum,ro a is the acceleration,k is the fiber's torsional that the data taking was resumed.Over a period of 20 days constant,and the overdots denote time derivatives.Figure 1 we operated the pendulum at various amplitudes ranging shows a numerical solution of Eq.(2)in comparison with a from approximately 13 nrad to 19 urad.A typical data measured trace.The simulation demonstrates that in the trace is shown as the solid line in Fig.1.The linear drift in MOND-like regime the period of oscillations is shorter the data is caused by a slow and constant relaxation of the than predicted by Newton's second law.just as is the torsion fiber.The noise at low frequencies (10 mHz)is case for stars far out in the galaxy which experience predominantly caused by Brownian excitation,while at similarly small forces. higher frequencies it is dominated by the optical readout. The instrument used for this test is the University of The angular position of the pendulum was measured Washington's equivalence principle apparatus,which con- with an autocollimator and was recorded every 2.74 s. sists of a torsion balance installed on an air bearing turn- The data analysis began by averaging every 20 data points. The data were then prefiltered with an algorithm that 800 identified large instantaneous changes in angular momen- tum(spikes).These impulses were often related to pressure 600 bursts of the ion pump,and sections containing such spikes were eliminated from the data,leading to 326 spike free 400 data sections of various lengths.We used the zero crossings of the second derivatives of the data to find the pendulum's equilibrium position and hence detect the linear drift which 200 was then subtracted from the raw(nonaveraged)data.To each section of this drift corrected data we fit a variable frequency sinusoid using a standard Levenberg-Marquardt technique [7].For each section we obtain the measured -200 frequency and amplitude and their corresponding uncertainties. .400 0 500 1000 1500 To convert the measured angular variables to linear vari- time(s) ables we used the mean effective radius r.=0.023 m, calculated from the pendulum's mass distribution.Com- FIG.I (color online).The solid line shows a typical measure- bining this radius with the measured amplitudes A and ment of the angular position of the torsion pendulum.The frequencies @/(27),we calculate the maximum force upward drift in the data is due to a slow unwinding of the torsion using Hooke's law,F AK/re,and the maximum accel- fiber.The noise in the measured trace is due to Brownian eration for the torsion pendulum,which occurs at the turn- excitation and readout noise.For purposes of comparison the simulated motion of the pendulum in a MOND-like regime with ing points and is given by a =Ar@2.Figure 2 shows the ao =1.0 X 10-12 m/s2 is plotted with a dashed line.Note that inferred accelerations versus force for all fitted data sec- the MOND-like dynamics would result in a much shorter period tions.Also shown is the deviation in acceleration and force of oscillation. from F=ma with m as the only fit parameter.Our data 150801-2can be made sufficiently long, so that the free torsional period would be altered. Therefore measuring the pendu￾lum’s period as a function of amplitude is a direct test of Newton’s second law. In the simplified case of a pendulum where all the mass is concentrated at one radius, as for a hollow cylinder with radius r, a MOND-like free equation of motion relates the acceleration a to the inertial torque on the pendulum : I; a; a0
Ia r
a=a0; (1) where I is the moment of inertia of the torsion pendulum. For a pendulum with an arbitrary mass distribution given by the radial mass density r the equation of motion implied by (1) is then
Z
jr
j=a0rr2dV 
 
0: (2) Here  is the angular displacement of the torsion pendu￾lum, r

a is the acceleration,  is the fiber’s torsional constant, and the overdots denote time derivatives. Figure 1 shows a numerical solution of Eq. (2) in comparison with a measured trace. The simulation demonstrates that in the MOND-like regime the period of oscillations is shorter than predicted by Newton’s second law, just as is the case for stars far out in the galaxy which experience similarly small forces. The instrument used for this test is the University of Washington’s equivalence principle apparatus, which con￾sists of a torsion balance installed on an air bearing turn￾table. The pendulum is suspended from a 1.07 m long, 20
m thick tungsten wire, with 
2:36 109 N m=rad. The natural period of the pendulum is 795 s and the amplitude decay time is 15 days, correspond￾ing to a quality factor, Q, of approximately 5000. The pendulum is suspended inside a vacuum chamber at a pressure of 105 Pa, maintained by an ion pump. Before each measurement the torsion pendulum was actively damped to very small amplitudes by rotating the turntable on which the torsion balance is installed. The turntable was then kept stationary and the torsional period was measured as a function of amplitude. The damping was necessary since the pendulum gained on average a torsional amplitude of about 60 nrad in approximately one period, mostly due to Brownian excitation in the fiber. Once the pendulum gained a substantial amplitude the data taking was stopped. The acquired torsional amplitude was removed by instantly rotating the turntable so that no energy remained stored in the twist of the fiber, and after that the data taking was resumed. Over a period of 20 days we operated the pendulum at various amplitudes ranging from approximately 13 nrad to 19
rad. A typical data trace is shown as the solid line in Fig. 1. The linear drift in the data is caused by a slow and constant relaxation of the torsion fiber. The noise at low frequencies ( 10 mHz) is predominantly caused by Brownian excitation, while at higher frequencies it is dominated by the optical readout. The angular position of the pendulum was measured with an autocollimator and was recorded every 2.74 s. The data analysis began by averaging every 20 data points. The data were then prefiltered with an algorithm that identified large instantaneous changes in angular momen￾tum (spikes). These impulses were often related to pressure bursts of the ion pump, and sections containing such spikes were eliminated from the data, leading to 326 spike free data sections of various lengths. We used the zero crossings of the second derivatives of the data to find the pendulum’s equilibrium position and hence detect the linear drift which was then subtracted from the raw (nonaveraged) data. To each section of this drift corrected data we fit a variable frequency sinusoid using a standard Levenberg-Marquardt technique [7]. For each section we obtain the measured frequency and amplitude and their corresponding uncertainties. To convert the measured angular variables to linear vari￾ables we used the mean effective radius re
0:023 m, calculated from the pendulum’s mass distribution. Com￾bining this radius with the measured amplitudes A and frequencies !=2, we calculate the maximum force using Hooke’s law, F
A=re , and the maximum accel￾eration for the torsion pendulum, which occurs at the turn￾ing points and is given by a
Are!2. Figure 2 shows the inferred accelerations versus force for all fitted data sec￾tions. Also shown is the deviation in acceleration and force from F
ma with m as the only fit parameter. Our data -400 -200 0 200 400 600 800 0 500 1000 1500 angle (nrad) time (s) FIG. 1 (color online). The solid line shows a typical measure￾ment of the angular position of the torsion pendulum. The upward drift in the data is due to a slow unwinding of the torsion fiber. The noise in the measured trace is due to Brownian excitation and readout noise. For purposes of comparison the simulated motion of the pendulum in a MOND-like regime with a0
1:0 1012 m=s2 is plotted with a dashed line. Note that the MOND-like dynamics would result in a much shorter period of oscillation. PRL 98, 150801 (2007) PHYSICAL REVIEW LETTERS week ending 13 APRIL 2007 150801-2