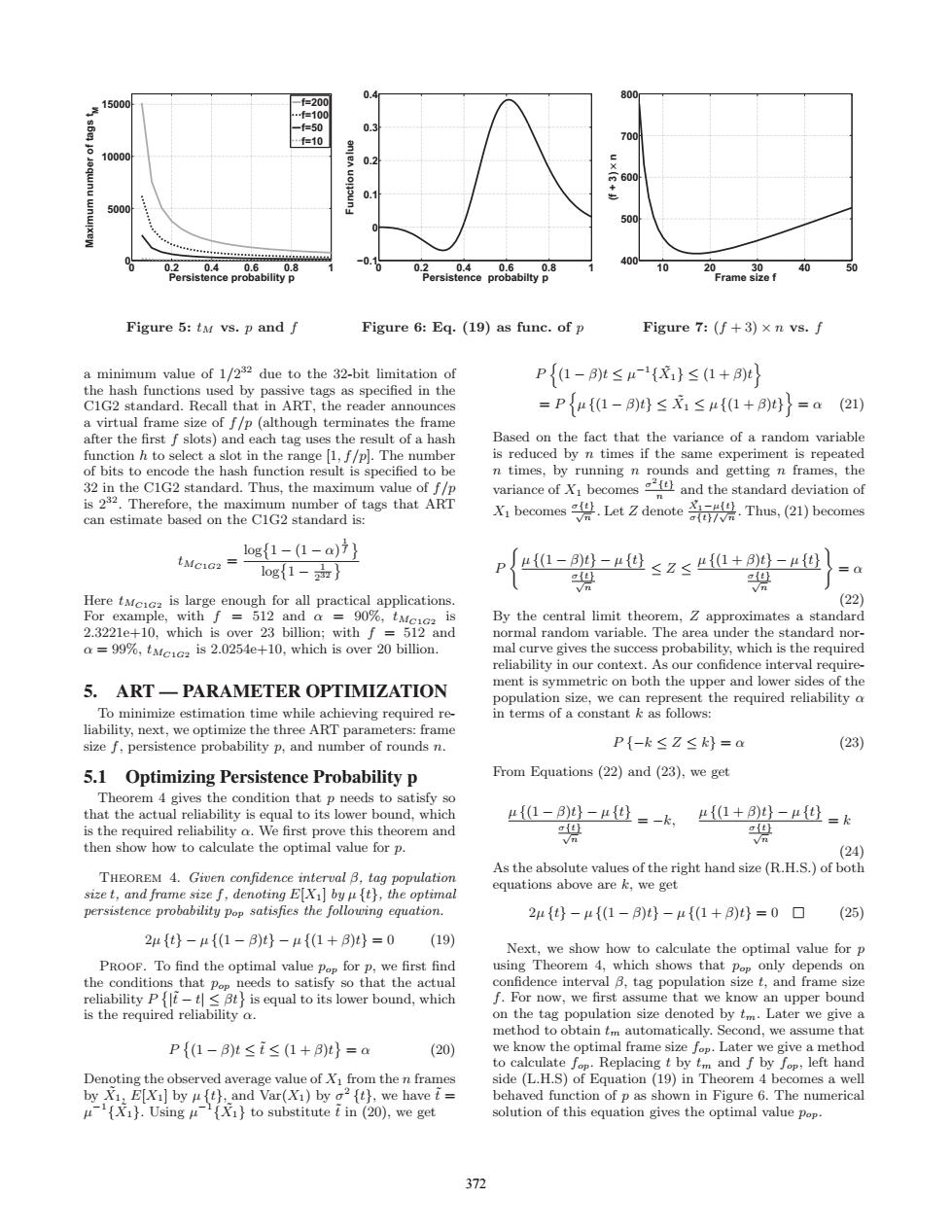
-f=200 0.4 800 15000 .f=100 .f=50 0.3 f=10 700 0 10000 0.2 7600 5000 500 0.2 0.4 0.6 0. 0.2 0.4 0.6 0.8 400 0.8 10 20 30 40 50 Persistence probability p Persistence probabilty p Frame size f Figure 5:tM vs.p and f Figure 6:Eq.(19)as func.of p Figure7:(f+3)×nvs.f a minimum value of 1/232 due to the 32-bit limitation of P{1-Bt≤{X}≤(1+B)} the hash functions used by passive tags as specified in the C1G2 standard.Recall that in ART,the reader announces =Pμ{1-B)≤X1≤4{(1+B)〉=a(21) a virtual frame size of f/p(although terminates the frame after the first f slots)and each tag uses the result of a hash Based on the fact that the variance of a random variable function h to select a slot in the range [1,f/p).The number is reduced by n times if the same experiment is repeated of bits to encode the hash function result is specified to be n times,by running n rounds and getting n frames,the 32 in the C1G2 standard.Thus,the maximum value of f/p variance of Xi becomes and the standard deviation of is 232.Therefore,the maximum number of tags that ART Xi becomes Let Zdenote Thus,(21)becomes can estimate based on the C1G2 standard is: aft/vn l1og{1-(1-a)7} 1og{1-2应} L-8-μ&≤Z≤+80-世 ot ait Q Here tcic is large enough for all practical applications. (22 For example,with f =512 and a 90%,tMcic2 is By the central limit theorem,Z approximates a standard 2.3221e+10,which is over 23 billion;with f 512 and normal random variable.The area under the standard nor- =99%,tcc is 2.0254e+10,which is over 20 billion. mal curve gives the success probability,which is the required reliability in our context.As our confidence interval require 5.ART-PARAMETER OPTIMIZATION ment is symmetric on both the upper and lower sides of the population size,we can represent the required reliability a To minimize estimation time while achieving required re- in terms of a constant k as follows: liability,next,we optimize the three ART parameters:frame size f,persistence probability p,and number of rounds n. P{-k≤Z≤k}=a (23) 5.1 Optimizing Persistence Probability p From Equations (22)and (23),we get Theorem 4 gives the condition that p needs to satisfy so that the actual reliability is equal to its lower bound,which 4{但-B4-世=-k, 4{但+B)-4=K is the required reliability a.We first prove this theorem and 碧 then show how to calculate the optimal value for p. (24) As the absolute values of the right hand size (R.H.S.)of both THEOREM 4.Given confidence interval B,tag population equations above are k,we get size t,and frame size f,denoting EX]by uith,the optimal persistence probability pop satisfies the following equation. 2μ{母-4{(1-)t}-μ{(1+B)t)=0▣ (25) 2μ{t-μ{(1-B)号-μ{(1+3)}=0(19) Next,we show how to calculate the optimal value for p PROOF.To find the optimal value pop for p,we first find using Theorem 4,which shows that pop only depends on the conditions that pop needs to satisfy so that the actual confidence interval B,tag population size t,and frame size reliability Pt-t<Bt is equal to its lower bound,which f.For now,we first assume that we know an upper bound is the required reliability a. on the tag population size denoted by tm.Later we give a method to obtain tm automatically.Second,we assume that P{(1-B)t≤t≤(1+B)t}=a (20 we know the optimal frame size fop.Later we give a method to calculate fop.Replacing t by tm and f by fop,left hand Denoting the observed average value of Xi from the n frames side (L.H.S)of Equation (19)in Theorem 4 becomes a well by X1.E[Xi]by uft),and Var(X1)by o2{t),we have t behaved function of p as shown in Figure 6.The numerical X1).Using [X1}to substitute i in (20),we get solution of this equation gives the optimal value pop. 3720 0.2 0.4 0.6 0.8 1 0 5000 10000 15000 Persistence probability p Maximum number of tags tM f=200 f=100 f=50 f=10 Figure 5: tM vs. p and f 0 0.2 0.4 0.6 0.8 1 −0.1 0 0.1 0.2 0.3 0.4 Persistence probabilty p Function value Figure 6: Eq. (19) as func. of p 10 20 30 40 50 400 500 600 700 800 Frame size f (f + 3) × n Figure 7: (f + 3) × n vs. f a minimum value of 1/232 due to the 32-bit limitation of the hash functions used by passive tags as specified in the C1G2 standard. Recall that in ART, the reader announces a virtual frame size of f /p (although terminates the frame after the first f slots) and each tag uses the result of a hash function h to select a slot in the range [1, f /p]. The number of bits to encode the hash function result is specified to be 32 in the C1G2 standard. Thus, the maximum value of f /p is 232. Therefore, the maximum number of tags that ART can estimate based on the C1G2 standard is: tMC1G2 = log 1 − (1 − α) 1 f log 1 − 1 232 Here tMC1G2 is large enough for all practical applications. For example, with f = 512 and α = 90%, tMC1G2 is 2.3221e+10, which is over 23 billion; with f = 512 and α = 99%, tMC1G2 is 2.0254e+10, which is over 20 billion. 5. ART — PARAMETER OPTIMIZATION To minimize estimation time while achieving required re￾liability, next, we optimize the three ART parameters: frame size f, persistence probability p, and number of rounds n. 5.1 Optimizing Persistence Probability p Theorem 4 gives the condition that p needs to satisfy so that the actual reliability is equal to its lower bound, which is the required reliability α. We first prove this theorem and then show how to calculate the optimal value for p. Theorem 4. Given confidence interval β, tag population size t, and frame size f, denoting E[X1] by μ {t}, the optimal persistence probability pop satisfies the following equation. 2μ {t} − μ {(1 − β)t} − μ {(1 + β)t} = 0 (19) Proof. To find the optimal value pop for p, we first find the conditions that pop needs to satisfy so that the actual reliability P |t ˜− t| ≤ βt is equal to its lower bound, which is the required reliability α. P (1 − β)t ≤ t ˜≤ (1 + β)t = α (20) Denoting the observed average value of X1 from the n frames by X˜1, E[X1] by μ {t}, and Var(X1) by σ2 {t}, we have t ˜= μ−1{X˜1}. Using μ−1{X˜1} to substitute t ˜ in (20), we get P  (1 − β)t ≤ μ−1 {X˜1} ≤ (1 + β)t  = P  μ {(1 − β)t} ≤ X˜1 ≤ μ {(1 + β)t}  = α (21) Based on the fact that the variance of a random variable is reduced by n times if the same experiment is repeated n times, by running n rounds and getting n frames, the variance of X1 becomes σ2{t} n and the standard deviation of X1 becomes σ{t} √n . Let Z denote X˜1−μ{t} σ{t}/ √n . Thus, (21) becomes P  μ {(1 − β)t} − μ {t} σ{t} √n ≤ Z ≤ μ {(1 + β)t} − μ {t} σ{t} √n  = α (22) By the central limit theorem, Z approximates a standard normal random variable. The area under the standard nor￾mal curve gives the success probability, which is the required reliability in our context. As our confidence interval require￾ment is symmetric on both the upper and lower sides of the population size, we can represent the required reliability α in terms of a constant k as follows: P {−k ≤ Z ≤ k} = α (23) From Equations (22) and (23), we get μ {(1 − β)t} − μ {t} σ{t} √n = −k, μ {(1 + β)t} − μ {t} σ{t} √n = k (24) As the absolute values of the right hand size (R.H.S.) of both equations above are k, we get 2μ {t} − μ {(1 − β)t} − μ {(1 + β)t} = 0 (25) Next, we show how to calculate the optimal value for p using Theorem 4, which shows that pop only depends on confidence interval β, tag population size t, and frame size f. For now, we first assume that we know an upper bound on the tag population size denoted by tm. Later we give a method to obtain tm automatically. Second, we assume that we know the optimal frame size fop. Later we give a method to calculate fop. Replacing t by tm and f by fop, left hand side (L.H.S) of Equation (19) in Theorem 4 becomes a well behaved function of p as shown in Figure 6. The numerical solution of this equation gives the optimal value pop. 372