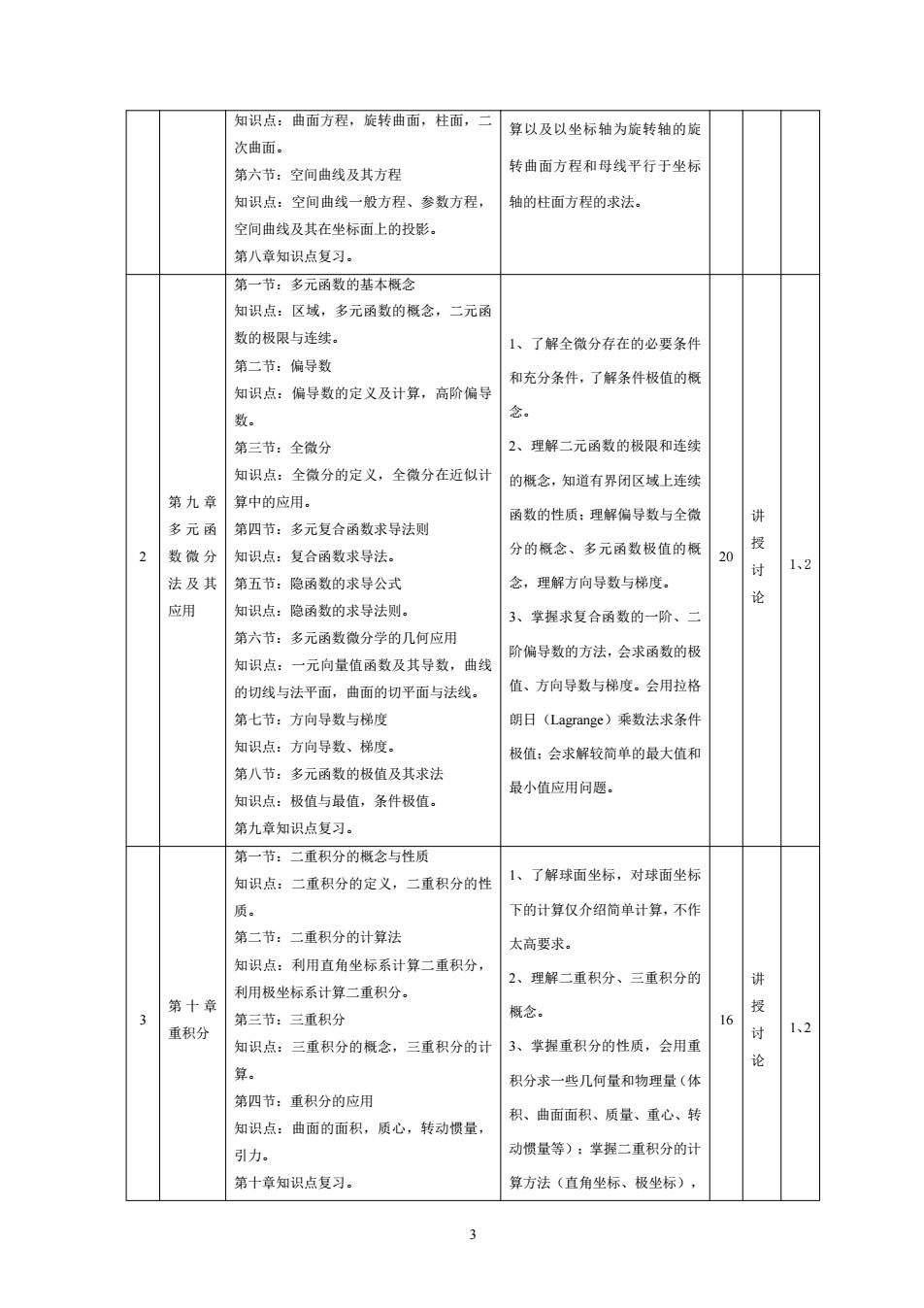
知识点：曲面方程，旋转曲面，柱面，算以及以坐标轴为旋转轴的 次曲面。 第六节：空间曲线及其方程 转曲面方程和母线平行于坐标 知识点：空间曲线一般方程、参数方程， 轴的柱面方程的求法。 空间曲线及其在坐标面上的投影。 第八章知识点复习。 第一节：多元函数的本概念 知识点：区域，多元函数的概念，二元函 数的极跟与连续。 1、了解全微分存在的必要条件 第二节：偏导数 和充分条件，了解条件极值的概 知识点：偏导数的定义及计算，高阶偏导 第三节：全微分 2、理解二元函数的极限和连续 知识点：全微分的定义，全微分在近似计 的概念，知道有界闭区域上连续 第九章算中的应用。 函数的性质：理解偏导数与全微 多元函 第四节：多元复合函数求导法 2数微分知识点，复合函数求导法。 分的概念、名元函数极值的椒 法及其 第五节：隐函数的求导公式 念，理解方向导数与梯度。 12 论 应用 知识点：隐函数的求导法则 3、掌握求复合函数的一阶、 第六节：多元函数微分学的几何应用 知识点：一元向量值函数及其导数，曲线 阶偏导数的方法，会求函数的极 的切线与法平面，曲面的切平面与法线， 值、方向导数与梯度。会用拉格 第七节：方向导数与梯度 朗日(Lagrange)乘数法求条件 知识点：方向导数、梯度. 极值：会求解较简单的最大值利 第八节：多元函数的极值及其求法 知识点：极值与最值，条件极值。 最小值应用问题。 第九章知识点复习。 第一节：一重积分的概多与性质 知识点 二重积分的定义， 二重积分的性 1、了解球面坐标，对球面坐标 质。 下的计算仅介绍简单计算，不作 第二节：二重积分的计算法 太高要求。 知识点：利用直角坐标系计算二重积分 利用极坐标系计算二重积分。 2、理解二重积分、三重积分的 3 第十章 授 第三节：三重积分 16 重积分 知识点：三重积分的概念， 三重积分的计 3、掌握重积分的性质，会用重 论 积分求一些几何量和物理量（使 第四节：重积分的应用 知识点：曲面的面积，质心，转动惯量 积、曲面面积、质量、重心、转 引力。 动惯量等)：掌握二重积分的计 第十章知识点复习。 算方法（直角坐标、极坐标）， 3 知识点：曲面方程，旋转曲面，柱面，二 次曲面。 第六节：空间曲线及其方程 知识点：空间曲线一般方程、参数方程， 空间曲线及其在坐标面上的投影。 第八章知识点复习。 算以及以坐标轴为旋转轴的旋 转曲面方程和母线平行于坐标 轴的柱面方程的求法。 2 第 九 章 多 元 函 数 微 分 法 及 其 应用 第一节：多元函数的基本概念 知识点：区域，多元函数的概念，二元函 数的极限与连续。 第二节：偏导数 知识点：偏导数的定义及计算，高阶偏导 数。 第三节：全微分 知识点：全微分的定义，全微分在近似计 算中的应用。 第四节：多元复合函数求导法则 知识点：复合函数求导法。 第五节：隐函数的求导公式 知识点：隐函数的求导法则。 第六节：多元函数微分学的几何应用 知识点：一元向量值函数及其导数，曲线 的切线与法平面，曲面的切平面与法线。 第七节：方向导数与梯度 知识点：方向导数、梯度。 第八节：多元函数的极值及其求法 知识点：极值与最值，条件极值。 第九章知识点复习。 1、了解全微分存在的必要条件 和充分条件，了解条件极值的概 念。 2、理解二元函数的极限和连续 的概念，知道有界闭区域上连续 函数的性质；理解偏导数与全微 分的概念、多元函数极值的概 念，理解方向导数与梯度。 3、掌握求复合函数的一阶、二 阶偏导数的方法，会求函数的极 值、方向导数与梯度。会用拉格 朗日（Lagrange）乘数法求条件 极值；会求解较简单的最大值和 最小值应用问题。 20 讲 授 讨 论 1、2 3 第 十 章 重积分 第一节：二重积分的概念与性质 知识点：二重积分的定义，二重积分的性 质。 第二节：二重积分的计算法 知识点：利用直角坐标系计算二重积分， 利用极坐标系计算二重积分。 第三节：三重积分 知识点：三重积分的概念，三重积分的计 算。 第四节：重积分的应用 知识点：曲面的面积，质心，转动惯量， 引力。 第十章知识点复习。 1、了解球面坐标，对球面坐标 下的计算仅介绍简单计算，不作 太高要求。 2、理解二重积分、三重积分的 概念。 3、掌握重积分的性质，会用重 积分求一些几何量和物理量（体 积、曲面面积、质量、重心、转 动惯量等）；掌握二重积分的计 算方法（直角坐标、极坐标）， 16 讲 授 讨 论 1、2