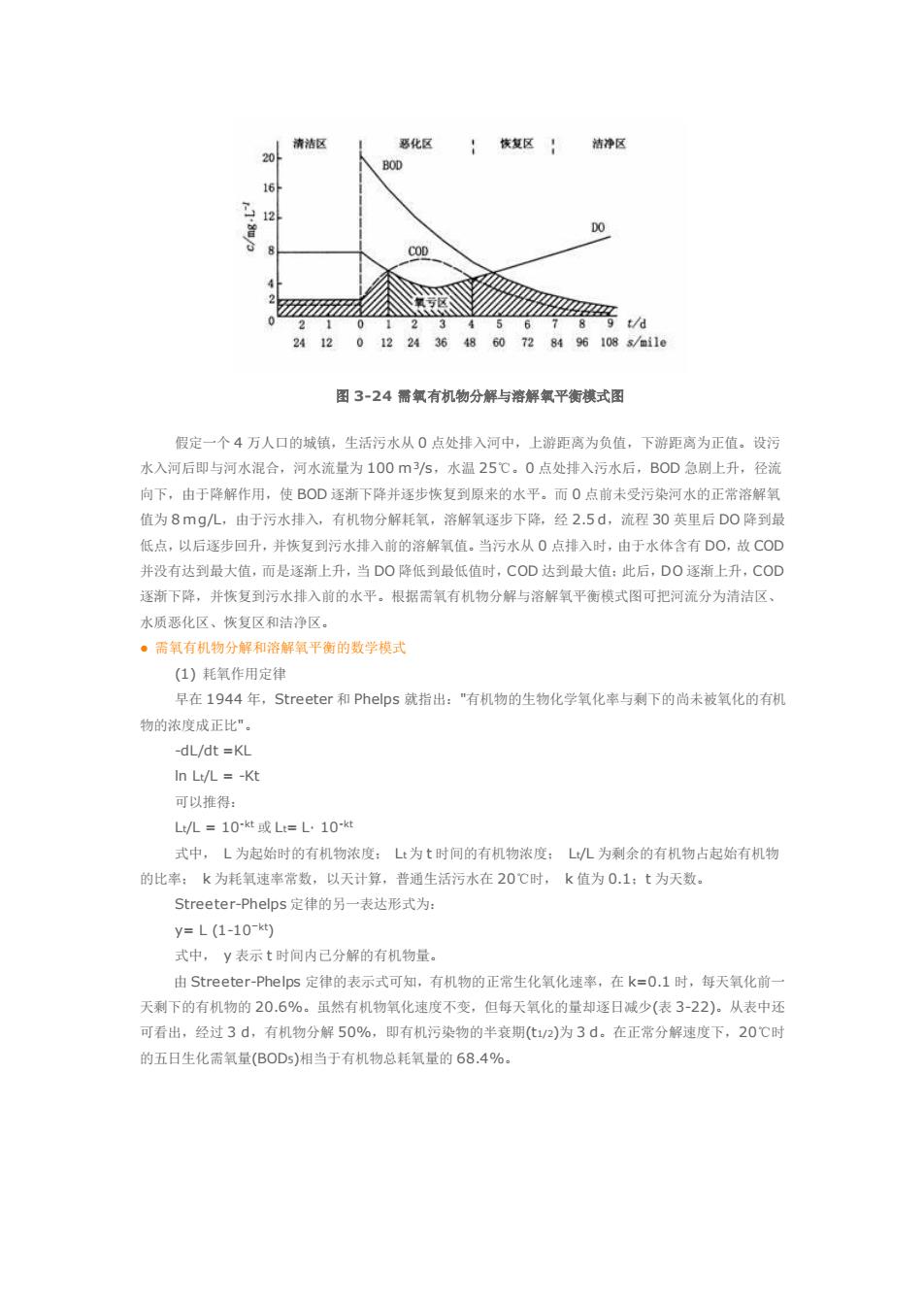
清洁区 化区 恢复区！裤净区 B00 00 5 a 241201224364860728496108x/e11e 图3-24氧有机物分解与溶解平衡模式图 假定一个4万人口的城镇，生活污水从0点处排入河中，上游距离为负值，下游距离为正位。设污 水入河后即与河水混合，河水流量为100m35,水温25℃。0点处排入污水后，B0D急副上升，径流 向下，由于降解作用，使BOD逐下降并逐步恢复到原来的水平。而0点前未受污染河水的正常溶解 值为8mg几，由于污水挂入，有机物分解耗氧，溶解氧逐步下降，经2.5d,流程30英里后D0降到直 低点，以后逐步回升，并恢复到污水棒入前的溶解氧值，当污水从0点排入时，由于水体含有DO,故COD 并没有达到最大值，而是逐渐上升，当D0降低到最低值时，COD达到最大值：此后，D0逐渐上升，COD 逐渐下降，并恢复到污水排入前的水平，根据需氧有机物分解与溶解氧平衡模式图可把河流分为清洁区 水质恶化区、核写区和洁净区， 。需氧有机物分解和溶解氧平商的数学模式 (1)耗氧作用定 早在1944年，Streeter和Phelps就指出："有机物的生物化学氧化率与剩下的尚未被氧化的有机 物的浓度成正比”。 -dL/dt=KL In Lt/L =-Kt 可以推得 L=10或L=L10 式中，L为起始时的有机物浓度：L:为t时间的有机物浓度：/几为剩余的有机物占起始有机物 的比率：k为耗氧速率常数，以天计算，普通生活污水在20C时，k值为0.1：t为天数。 Streeter-Phelps定律的另一表达形式为： y=L(1-10-) 式中，y表示t时间内已分解的有机物量。 由Streeter--Phelps定律的表示式可知，有机物的正常生化氧化速率，在k=0.1时，每天氧化前 天剩下的有机物的20.6%。虽然有机物氧化速度不变，但每天氧化的量却逐日减少（表3-22）.从表中还 可看出，经过3d,有机物分解50%，即有机污染物的半衰期化12)为3d。在正常分解速度下，20℃时 的五日生化需氧量(B0Ds)相当于有机物总耗氧量的68.4%图 3-24 需氧有机物分解与溶解氧平衡模式图 假定一个 4 万人口的城镇，生活污水从 0 点处排入河中，上游距离为负值，下游距离为正值。设污 水入河后即与河水混合，河水流量为 100 m3/s，水温 25℃。0 点处排入污水后，BOD 急剧上升，径流 向下，由于降解作用，使 BOD 逐渐下降并逐步恢复到原来的水平。而 0 点前未受污染河水的正常溶解氧 值为 8 mg/L，由于污水排入，有机物分解耗氧，溶解氧逐步下降，经 2.5 d，流程 30 英里后 DO 降到最 低点，以后逐步回升，并恢复到污水排入前的溶解氧值。当污水从 0 点排入时，由于水体含有 DO，故 COD 并没有达到最大值，而是逐渐上升，当 DO 降低到最低值时，COD 达到最大值；此后，DO 逐渐上升，COD 逐渐下降，并恢复到污水排入前的水平。根据需氧有机物分解与溶解氧平衡模式图可把河流分为清洁区、 水质恶化区、恢复区和洁净区。 ● 需氧有机物分解和溶解氧平衡的数学模式 (1) 耗氧作用定律 早在 1944 年，Streeter 和 Phelps 就指出："有机物的生物化学氧化率与剩下的尚未被氧化的有机 物的浓度成正比"。 -dL/dt =KL ln Lt/L = -Kt 可以推得： Lt/L = 10-kt 或 Lt= L· 10-kt 式中， L 为起始时的有机物浓度； Lt为 t 时间的有机物浓度； Lt/L 为剩余的有机物占起始有机物 的比率； k 为耗氧速率常数，以天计算，普通生活污水在 20℃时， k 值为 0.1；t 为天数。 Streeter-Phelps 定律的另一表达形式为： y= L (1-10－kt) 式中， y 表示 t 时间内已分解的有机物量。 由 Streeter-Phelps 定律的表示式可知，有机物的正常生化氧化速率，在 k=0.1 时，每天氧化前一 天剩下的有机物的 20.6%。虽然有机物氧化速度不变，但每天氧化的量却逐日减少(表 3-22)。从表中还 可看出，经过 3 d，有机物分解 50%，即有机污染物的半衰期(t1/2)为 3 d。在正常分解速度下，20℃时 的五日生化需氧量(BOD5)相当于有机物总耗氧量的 68.4%