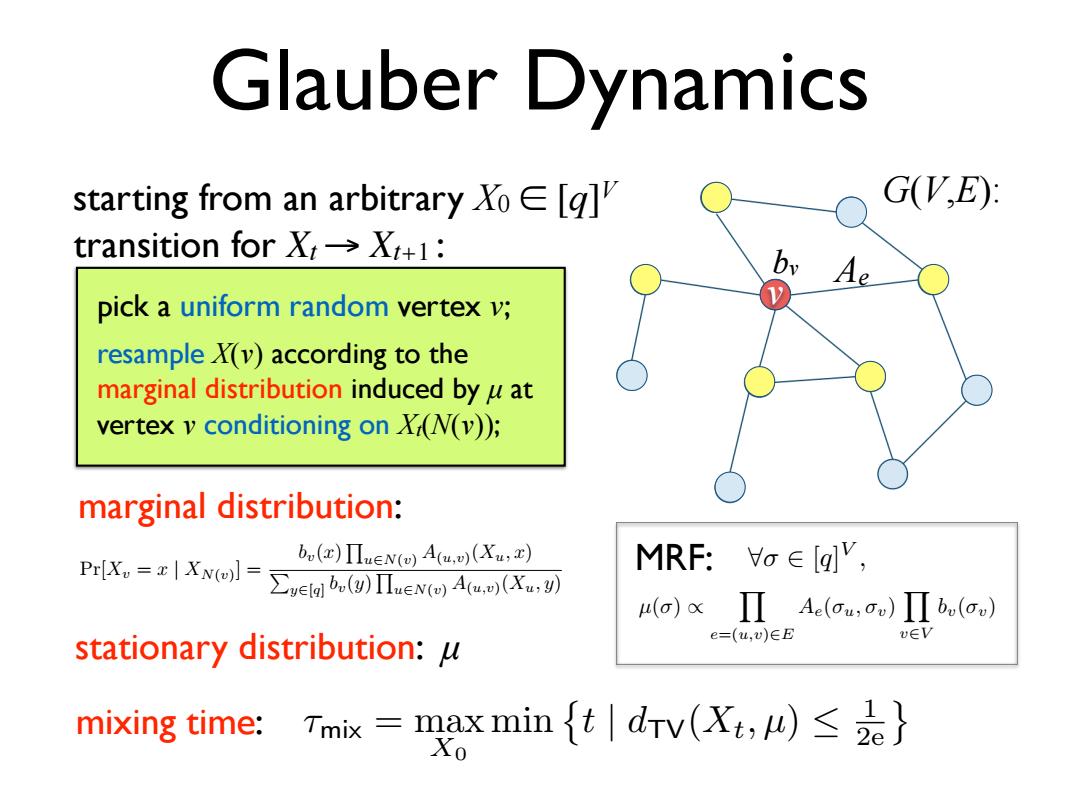
Glauber Dynamics starting from an arbitrary Xo E [g] G(V,E) transition for XX+1: pick a uniform random vertex v; resample X(v)according to the marginal distribution induced by u at vertex v conditioning on X(N(v)); marginal distribution: bo()IIEN()A(.)(Xu:) PrlX,=z|Xwol=ehb.IexoAeX, MRF:o∈g', u(o)xΠAe(o,o)Πb(a) v∈V stationary distribution:u e=(u,v)∈E mixing time::Tmix=max min{t|drv(Xt,)）≤2e} XoGlauber Dynamics G(V,E): pick a uniform random vertex v; resample X(v) according to the marginal distribution induced by µ at vertex v conditioning on Xt(N(v)); starting from an arbitrary X0 ∈ [q]V transition for Xt → Xt+1 : marginal distribution: Pr[Xv = x | XN(v)] = bv(x) Q u2N(v) A(u,v)(Xu, x) P y2[q] bv(y) Q u2N(v) A(u,v)(Xu, y) Ae bv v µ(￾) / Y e=(u,v)2E Ae(￾u, ￾v) Y v2V bv(￾v) MRF: 8￾ 2 [q] V , stationary distribution: µ mixing time: ⌧mix = max X0 min ￾ t | dTV(Xt, µ)  1 2e