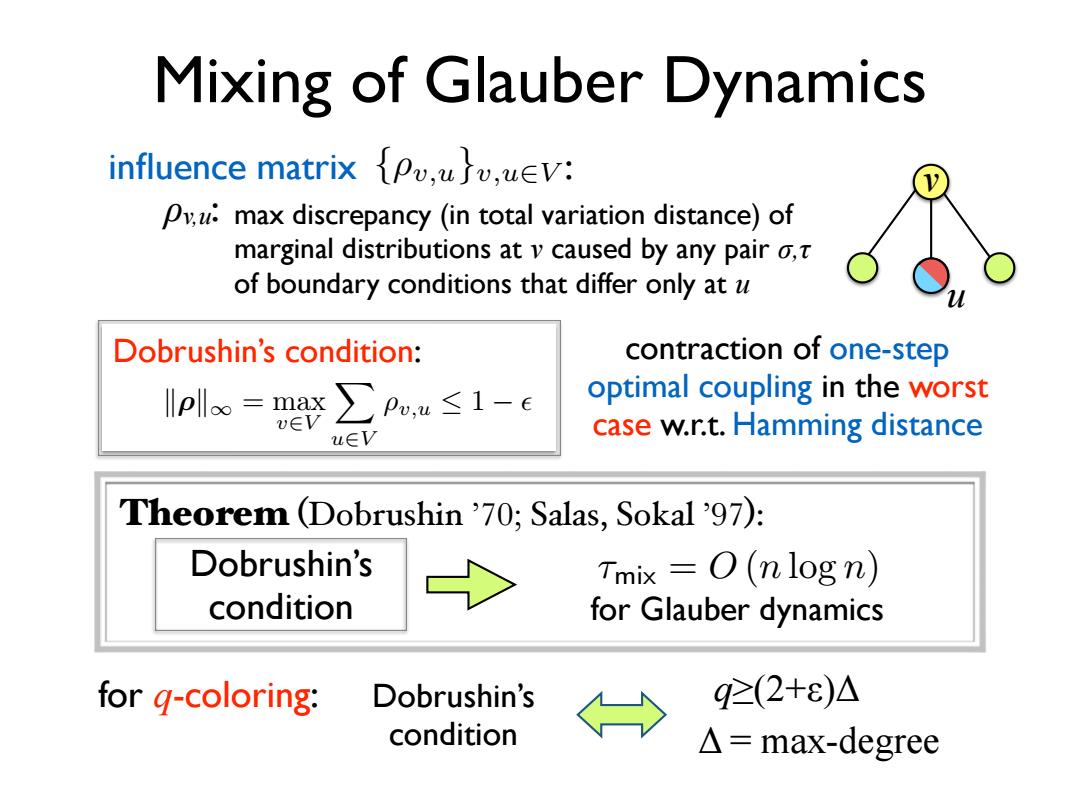
Mixing of Glauber Dynamics influence matrix [Po,u,uEv: Pv.u:max discrepancy (in total variation distance)of marginal distributions at v caused by any pair o,t of boundary conditions that differ only at u Dobrushin's condition: contraction of one-step Ipl=∑Pee≤1-e optimal coupling in the worst u∈V case w.r.t.Hamming distance Theorem (Dobrushin'70:Salas,Sokal'97): Dobrushin's Tmix =O(nlogn) condition for Glauber dynamics for g-coloring: Dobrushin's 92(2+ε)△ condition △=max-degreeMixing of Glauber Dynamics for q-coloring: Dobrushin’s q≥(2+ε)Δ condition Δ = max-degree u v influence matrix {⇢v,u }v,u2V : ρv,u: max discrepancy (in total variation distance) of marginal distributions at v caused by any pair σ,τ of boundary conditions that differ only at u Dobrushin’s condition: k⇢k1 = max v2V X u2V ⇢v,u  1 ￾ ✏ contraction of one-step optimal coupling in the worst case w.r.t. Hamming distance Theorem (Dobrushin ’70; Salas, Sokal ’97): Dobrushin’s condition for Glauber dynamics ⌧mix = O (n log n)