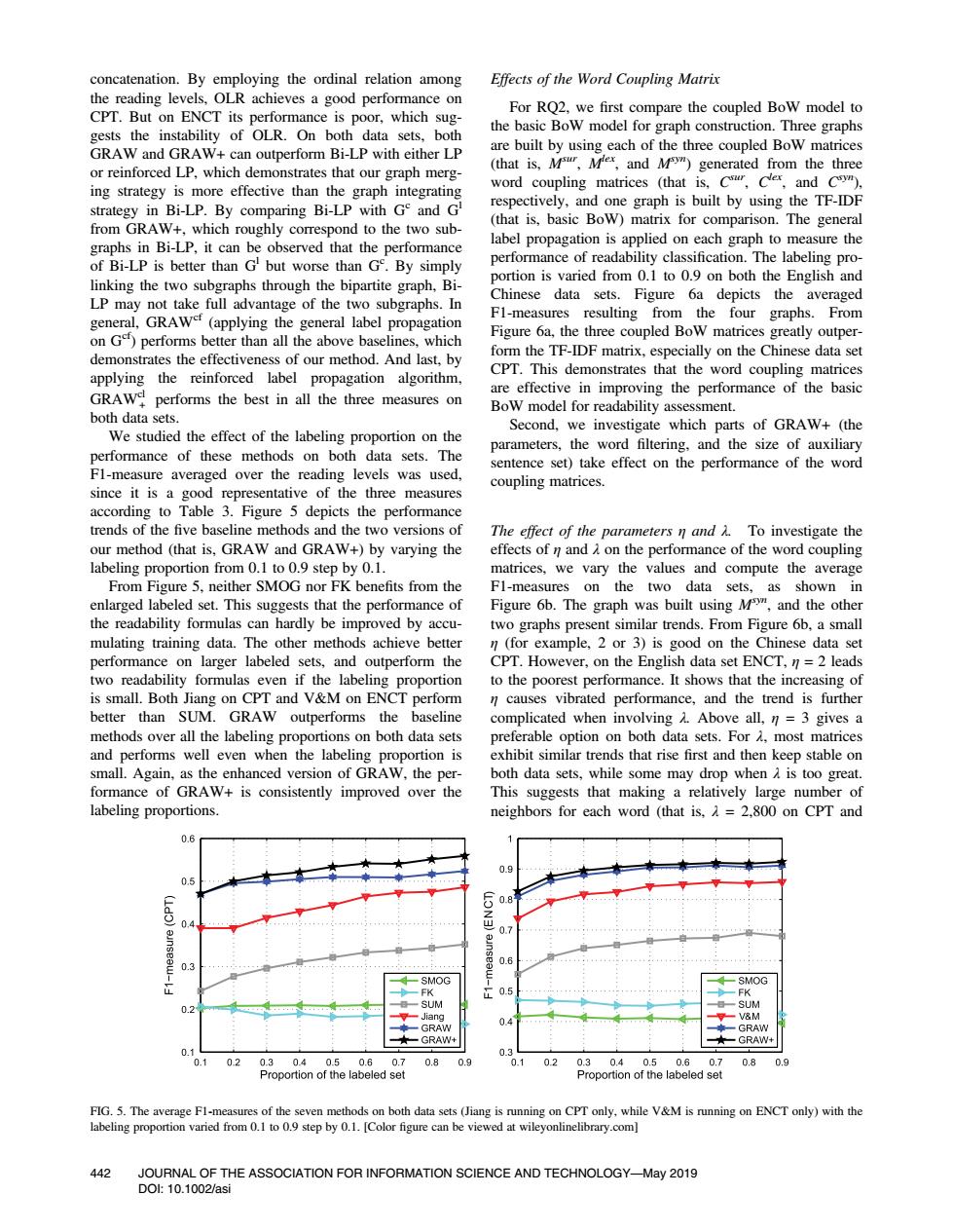
concatenation.By employing the ordinal relation among Effects of the Word Coupling Matrix the reading levels,OLR achieves a good performance on CPT.But on ENCT its performance is poor,which sug- For RQ2,we first compare the coupled BoW model to gests the instability of OLR.On both data sets,both the basic BoW model for graph construction.Three graphs GRAW and GRAW+can outperform Bi-LP with either LP are built by using each of the three coupled Bow matrices or reinforced LP,which demonstrates that our graph merg- (that is,Msur,Mlex,and M")generated from the three ing strategy is more effective than the graph integrating word coupling matrices (that is,C,Cler,and C). strategy in Bi-LP.By comparing Bi-LP with Ge and G respectively,and one graph is built by using the TF-IDF from GRAW+,which roughly correspond to the two sub- (that is,basic Bow)matrix for comparison.The general graphs in Bi-LP,it can be observed that the performance label propagation is applied on each graph to measure the of Bi-LP is better than G but worse than G.By simply performance of readability classification.The labeling pro- linking the two subgraphs through the bipartite graph,Bi- portion is varied from 0.1 to 0.9 on both the English and LP may not take full advantage of the two subgraphs.In Chinese data sets.Figure 6a depicts the averaged general,GRAWe (applying the general label propagation F1-measures resulting from the four graphs.From on Ge)performs better than all the above baselines,which Figure 6a,the three coupled BoW matrices greatly outper- demonstrates the effectiveness of our method.And last,by form the TF-IDF matrix,especially on the Chinese data set applying the reinforced label propagation algorithm, CPT.This demonstrates that the word coupling matrices GRAWe performs the best in all the three measures on are effective in improving the performance of the basic BoW model for readability assessment. both data sets. Second,we investigate which parts of GRAW+(the We studied the effect of the labeling proportion on the parameters,the word filtering,and the size of auxiliary performance of these methods on both data sets.The sentence set)take effect on the performance of the word F1-measure averaged over the reading levels was used, coupling matrices. since it is a good representative of the three measures according to Table 3.Figure 5 depicts the performance trends of the five baseline methods and the two versions of The effect of the parameters n and h.To investigate the our method (that is,GRAW and GRAW+)by varying the effects of n and A on the performance of the word coupling labeling proportion from 0.1 to 0.9 step by 0.1. matrices,we vary the values and compute the average From Figure 5,neither SMOG nor FK benefits from the Fl-measures on the two data sets,as shown in enlarged labeled set.This suggests that the performance of Figure 6b.The graph was built using M",and the other the readability formulas can hardly be improved by accu- two graphs present similar trends.From Figure 6b,a small mulating training data.The other methods achieve better n(for example,2 or 3)is good on the Chinese data set performance on larger labeled sets,and outperform the CPT.However,on the English data set ENCT,n=2 leads two readability formulas even if the labeling proportion to the poorest performance.It shows that the increasing of is small.Both Jiang on CPT and V&M on ENCT perform n causes vibrated performance,and the trend is further better than SUM.GRAW outperforms the baseline complicated when involving A.Above all,n=3 gives a methods over all the labeling proportions on both data sets preferable option on both data sets.For most matrices and performs well even when the labeling proportion is exhibit similar trends that rise first and then keep stable on small.Again,as the enhanced version of GRAW,the per- both data sets,while some may drop when A is too great. formance of GRAW+is consistently improved over the This suggests that making a relatively large number of labeling proportions. neighbors for each word (that is,A=2,800 on CPT and 0.6 0.8 0.4 0.7 0.3 ·SMOG SMOG 0.2 SUM SUM lan▣ V&M 04 GRAW GRAW GRAW GRAW+ 0.1 0.3 0.1 0.2 0.30.4 0.5 0.6 0.7 0.8 0.9 01 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Proportion of the labeled set Proportion of the labeled set FIG.5.The average F1-measures of the seven methods on both data sets (Jiang is running on CPT only,while V&M is running on ENCT only)with the labeling proportion varied from 0.1 to 0.9 step by 0.1.[Color figure can be viewed at wileyonlinelibrary.com] 442 JOURNAL OF THE ASSOCIATION FOR INFORMATION SCIENCE AND TECHNOLOGY-May 2019 D0l:10.1002/asiconcatenation. By employing the ordinal relation among the reading levels, OLR achieves a good performance on CPT. But on ENCT its performance is poor, which sug￾gests the instability of OLR. On both data sets, both GRAW and GRAW+ can outperform Bi-LP with either LP or reinforced LP, which demonstrates that our graph merg￾ing strategy is more effective than the graph integrating strategy in Bi-LP. By comparing Bi-LP with Gc and Gl from GRAW+, which roughly correspond to the two sub￾graphs in Bi-LP, it can be observed that the performance of Bi-LP is better than Gl but worse than Gc . By simply linking the two subgraphs through the bipartite graph, Bi￾LP may not take full advantage of the two subgraphs. In general, GRAWcf (applying the general label propagation on Gcf) performs better than all the above baselines, which demonstrates the effectiveness of our method. And last, by applying the reinforced label propagation algorithm, GRAWcl + performs the best in all the three measures on both data sets. We studied the effect of the labeling proportion on the performance of these methods on both data sets. The F1-measure averaged over the reading levels was used, since it is a good representative of the three measures according to Table 3. Figure 5 depicts the performance trends of the five baseline methods and the two versions of our method (that is, GRAW and GRAW+) by varying the labeling proportion from 0.1 to 0.9 step by 0.1. From Figure 5, neither SMOG nor FK benefits from the enlarged labeled set. This suggests that the performance of the readability formulas can hardly be improved by accu￾mulating training data. The other methods achieve better performance on larger labeled sets, and outperform the two readability formulas even if the labeling proportion is small. Both Jiang on CPT and V&M on ENCT perform better than SUM. GRAW outperforms the baseline methods over all the labeling proportions on both data sets and performs well even when the labeling proportion is small. Again, as the enhanced version of GRAW, the per￾formance of GRAW+ is consistently improved over the labeling proportions. Effects of the Word Coupling Matrix For RQ2, we first compare the coupled BoW model to the basic BoW model for graph construction. Three graphs are built by using each of the three coupled BoW matrices (that is, Msur, Mlex, and Msyn) generated from the three word coupling matrices (that is, Csur, Clex, and Csyn), respectively, and one graph is built by using the TF-IDF (that is, basic BoW) matrix for comparison. The general label propagation is applied on each graph to measure the performance of readability classification. The labeling pro￾portion is varied from 0.1 to 0.9 on both the English and Chinese data sets. Figure 6a depicts the averaged F1-measures resulting from the four graphs. From Figure 6a, the three coupled BoW matrices greatly outper￾form the TF-IDF matrix, especially on the Chinese data set CPT. This demonstrates that the word coupling matrices are effective in improving the performance of the basic BoW model for readability assessment. Second, we investigate which parts of GRAW+ (the parameters, the word filtering, and the size of auxiliary sentence set) take effect on the performance of the word coupling matrices. The effect of the parameters η and λ. To investigate the effects of η and λ on the performance of the word coupling matrices, we vary the values and compute the average F1-measures on the two data sets, as shown in Figure 6b. The graph was built using Msyn, and the other two graphs present similar trends. From Figure 6b, a small η (for example, 2 or 3) is good on the Chinese data set CPT. However, on the English data set ENCT, η = 2 leads to the poorest performance. It shows that the increasing of η causes vibrated performance, and the trend is further complicated when involving λ. Above all, η = 3 gives a preferable option on both data sets. For λ, most matrices exhibit similar trends that rise first and then keep stable on both data sets, while some may drop when λ is too great. This suggests that making a relatively large number of neighbors for each word (that is, λ = 2,800 on CPT and FIG. 5. The average F1-measures of the seven methods on both data sets (Jiang is running on CPT only, while V&M is running on ENCT only) with the labeling proportion varied from 0.1 to 0.9 step by 0.1. [Color figure can be viewed at wileyonlinelibrary.com] 442 JOURNAL OF THE ASSOCIATION FOR INFORMATION SCIENCE AND TECHNOLOGY—May 2019 DOI: 10.1002/asi