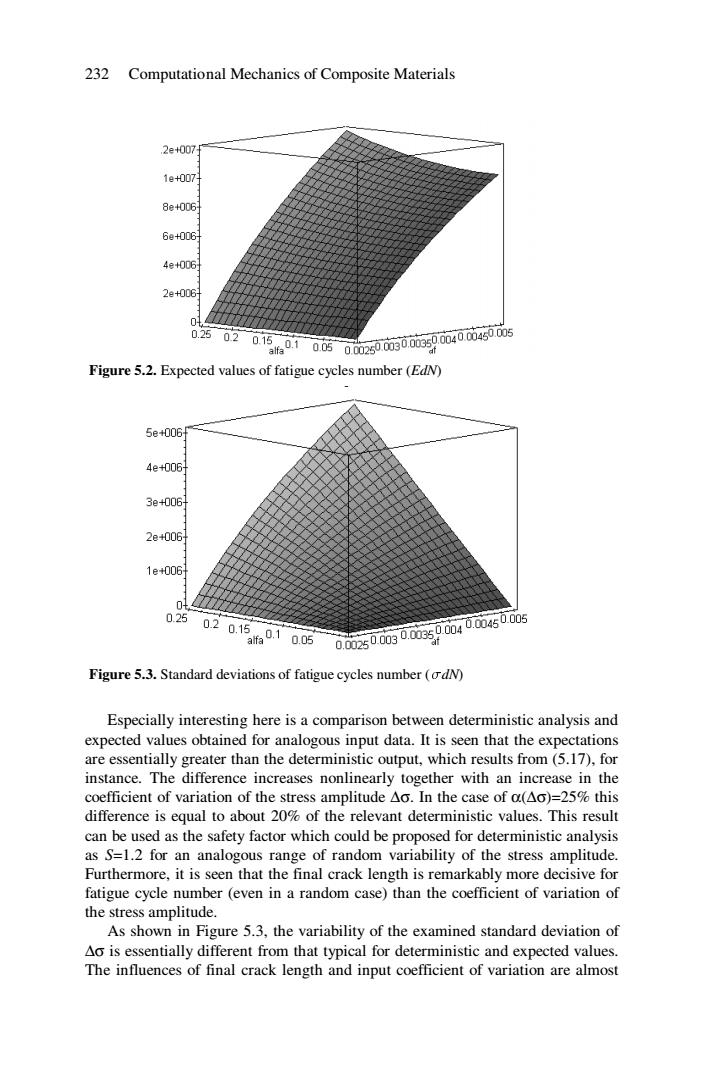
232 Computational Mechanics of Composite Materials 2e+007 1e+007 8e+006 6e+006 4e+006 2e+006 042 02站02d1500话00动0防009040045005 Figure 5.2.Expected values of fatigue cycles number (EdN) 5e+006 4e+006+ 3e+006+ 2e+006 1e+006 0.25 0201569100s0i500900io590040046005 Figure 5.3.Standard deviations of fatigue cycles number (odN) Especially interesting here is a comparison between deterministic analysis and expected values obtained for analogous input data.It is seen that the expectations are essentially greater than the deterministic output,which results from(5.17),for instance.The difference increases nonlinearly together with an increase in the coefficient of variation of the stress amplitude Ao.In the case of a(Ao)=25%this difference is equal to about 20%of the relevant deterministic values.This result can be used as the safety factor which could be proposed for deterministic analysis as S=1.2 for an analogous range of random variability of the stress amplitude. Furthermore,it is seen that the final crack length is remarkably more decisive for fatigue cycle number(even in a random case)than the coefficient of variation of the stress amplitude. As shown in Figure 5.3,the variability of the examined standard deviation of Ao is essentially different from that typical for deterministic and expected values. The influences of final crack length and input coefficient of variation are almost232 Computational Mechanics of Composite Materials Figure 5.2. Expected values of fatigue cycles number (EdN) Figure 5.3. Standard deviations of fatigue cycles number (sdN) Especially interesting here is a comparison between deterministic analysis and expected values obtained for analogous input data. It is seen that the expectations are essentially greater than the deterministic output, which results from (5.17), for instance. The difference increases nonlinearly together with an increase in the coefficient of variation of the stress amplitude ∆σ. In the case of α(∆σ)=25% this difference is equal to about 20% of the relevant deterministic values. This result can be used as the safety factor which could be proposed for deterministic analysis as S=1.2 for an analogous range of random variability of the stress amplitude. Furthermore, it is seen that the final crack length is remarkably more decisive for fatigue cycle number (even in a random case) than the coefficient of variation of the stress amplitude. As shown in Figure 5.3, the variability of the examined standard deviation of ∆σ is essentially different from that typical for deterministic and expected values. The influences of final crack length and input coefficient of variation are almost