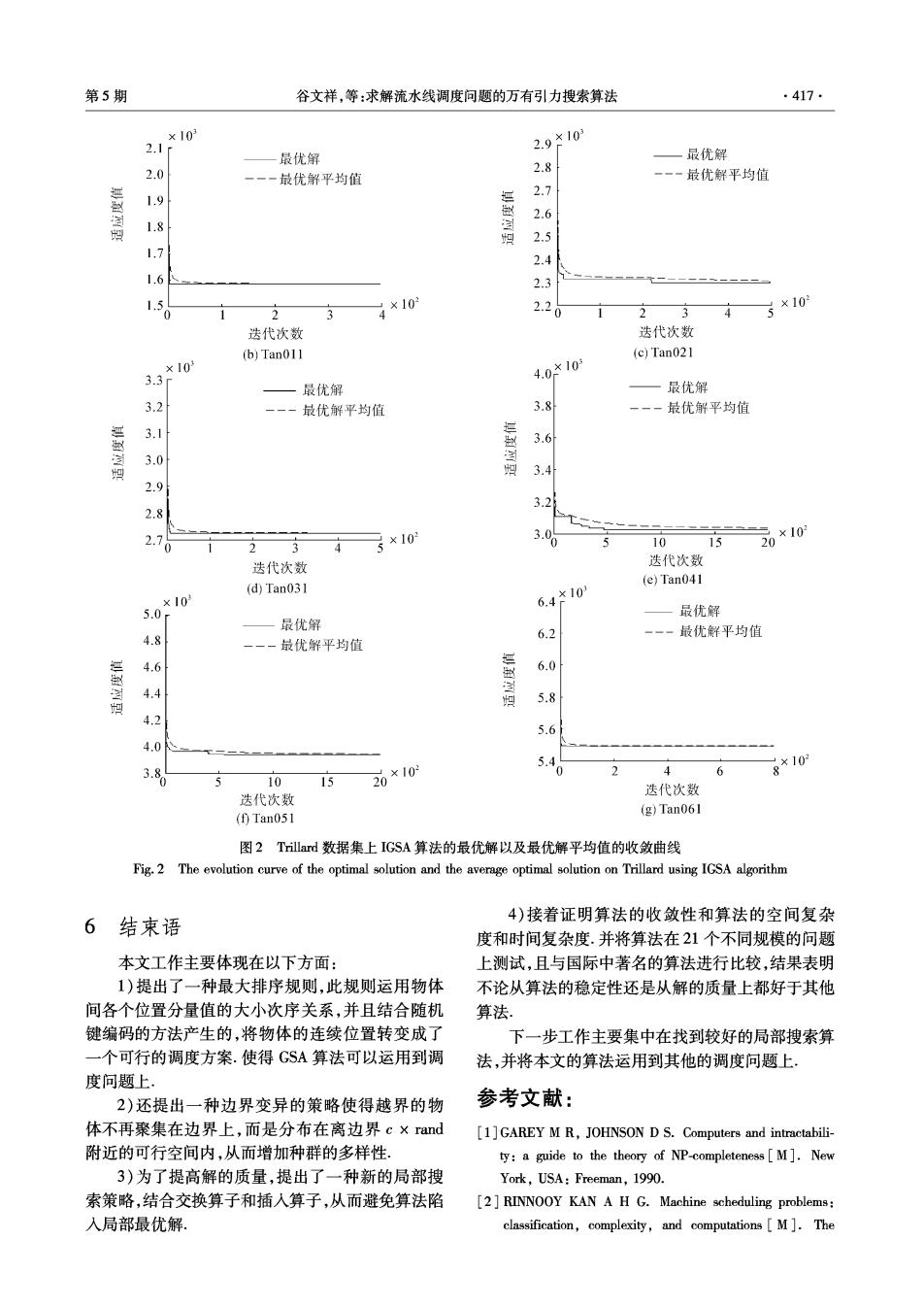
第5期 谷文祥，等：求解流水线调度问题的万有引力搜索算法 .417 10 2.1f 2.9×10 一最优解 ,最优解 2.0 2.8 最优解平均值 一一一最优解平均值 1.9 2.7 2.6 1.8 2.5 1.7 2.4 1.6 2.3 1.5 2 3 ×10 4 2.20 2 3 ×10 迭代次数 迭代次数 (b)Tan011 (c)Tan021 ×10 3.3 4.0*10 最优解 最优解 3.2 最优解平均值 3.8 -一一最优解平均值 3.1 3.6 3.0 3.4 2.9 3.2 2.8 2.10 ×10 3.0 10 20*10 迭代次数 迭代次数 (d)Tan031 (e)Tan041 0*0 6.4*10 最优解 最优解 4.8 最优解平均值 6.2 最优解平均值 4.6 到 6.0 4.4 5.8 4.2 5.6 4.0 3.8 20*10 5.40 2 6 8*10 5 10 15 迭代次数 迭代次数 (f)Tan051 (g)Tan061 图2 Trillard数据集上IGSA算法的最优解以及最优解平均值的收敛曲线 Fig.2 The evolution curve of the optimal solution and the average optimal solution on Trillard using IGSA algorithm 6结束语 4)接着证明算法的收敛性和算法的空间复杂 度和时间复杂度.并将算法在21个不同规模的问题 本文工作主要体现在以下方面： 上测试，且与国际中著名的算法进行比较，结果表明 1)提出了一种最大排序规则，此规则运用物体 不论从算法的稳定性还是从解的质量上都好于其他 间各个位置分量值的大小次序关系，并且结合随机 算法 键编码的方法产生的，将物体的连续位置转变成了 下一步工作主要集中在找到较好的局部搜索算 一个可行的调度方案.使得GSA算法可以运用到调 法，并将本文的算法运用到其他的调度问题上. 度问题上 2)还提出一种边界变异的策略使得越界的物 参考文献： 体不再聚集在边界上，而是分布在离边界c×rand [1]GAREY M R,JOHNSON D S.Computers and intractabili- 附近的可行空间内，从而增加种群的多样性， ty:a guide to the theory of NP-completeness [M].New 3)为了提高解的质量，提出了一种新的局部搜 York,USA:Freeman,1990. 索策略，结合交换算子和插入算子，从而避免算法陷 [2]RINNOOY KAN A H G.Machine scheduling problems: 入局部最优解。 classification,complexity,and computations[M].The