智能系统：求解流水线调度问题的万有引力搜索算法

第5卷第5期 智能系统学报 Vol.5 No.5 2010年10月 CAAI Transactions on Intelligent Systems 0ct.2010 doi:10.3969/i.issn.1673-4785.2010.05.006 求解流水线调度问题的万有引力搜索算法 谷文祥，李向涛，朱磊，周俊萍，胡艳梅 (东北师范大学计算机学院，吉林长春130117) 摘要：研究了以最大完工时间为目标的流水线调度问题，使用万有引力算法求解调度问题，提出了一种最大排序 规则，利用物体间各个位置分量值存在的大小次序关系，并结合随机键编码的方法产生，将物体的连续位置转变成 了一个可行的调度方案；提出了一种边界变异的策略使得越界的物体不再聚集在边界上，而是分布在边界附近的可 行空间内，从而增加种群的多样性；结合交换算子和插入算子提出了一种新的局部搜索算法，有效地避免了算法陷 入局部最优值，进一步提高了解的质量.最后证明了算法的收敛性，并且计算了算法的时间复杂度和空间复杂度，仿 真实验说明了所得算法的有效性， 关键词：万有引力搜索算法；流水线调度；局部搜索算法；边界变异；最大排序规则；最大完工时间 中图分类号：TP301.6文献标识码：A文章编号：16734785(2010)05-041108 A gravitational search algorithm for flow shop scheduling GU Wen-xiang,LI Xiang-tao,ZHU Lei,ZHOU Jun-ping,HU Yan-mei (Department of Computer Science,Northeast Normal University,Changchun 130117,China) Abstract:An improved gravitational search algorithm(IGSA)was proposed to solve the flow shop scheduling prob- lem with the objective of minimizing production time.First,to make a GSA suitable for permutation of the flow shop scheduling problem(PFSSP),a new largest-rank-rule based on a random key was introduced to convert the continuous position of the GSA into the discrete job permutation so that the GSA could be used for solving PFSSP. Second,a new boundary mutation was proposed.This operation stopped the agents which have mutations as a result of using the above method from gathering at the border.They were distributed at a feasible distance from the bound- ary.This improvement also improved the population diversity.Third,by combining the communicating operator and inserting operator,the new local search was designed to help the algorithm escape from the local minimum.Final- ly,the convergence of the iterative algorithm and its complexities in time and space were proven.Additionally, simulations and comparisons based on PFSSP benchmarks were carried out,which show that the proposed algorithm is both effective and efficient. Keywords:gravitational search algorithm;flow shop scheduling;local search;boundary mutation;largest rank rule;production time minimizing 流水线调度问题(flow shop scheduling problem, 法通常包括3种：精确算法34、启发式算法36以及 FSP)是许多实际生产调度过程的简化模型，它已经 元启发式算法8].精确算法一般仅仅适合于小规 被证明是NP-hard2.由于其重要的理论意义和工 模问题；构造启发式算法和提高式启发式算法虽然 程价值，FSP问题已成为目前调度问题研究的热点 能够解决部分大规模问题，但是解的质量往往不高； 之一.流水线调度是研究n个工件在m台机器上的 元启发式算法通过模仿自然界的某些现象和过程进 流水加工过程，同时约定：1)每个工件在每台机器 行优化，一般是从若干个解出发，通过对搜索空间的 上只能加工1次；2)每个工件的加工不能被中断； 不断搜索，直到达到一定的条件，最终获得该问题的 3)每台机器每次最多只能加工1个工件；4)每合机 最优解或者近似最优解.因此，元启发式算法成为了 器执行工件的顺序是相同的.目前求解该问题的方 求解流水线调度问题的主要方法， 万有引力搜索算法(GSA)9是由E.Rashedi 收稿日期：2010-0329. 和H.Nezamabadi--pour等在2009年提出的一种源 基金项目：国家自然科学基金资助项目(60473042,60573067,60803102) 于对物理学中的万有引力进行模拟的新的优化搜索 通信作者：李向涛.E-mail:li314@nenu.cdu.cm, 技术，与粒子群算法(PS0)相似，是一种元启发式算

412 智能系统学报 第5卷 法.它通过群体中各粒子之间的万有引力相互作用 在特定的时间t,定义作用在物体i和物体j之 产生的群体智能指导优化搜索，但是目前对于GSA 间的重力搜索表示为 算法的研究还很少.实验证明，GSA的收敛性明显 优于PS0、遗传算法(GA)等其他智能优化算法，但 r=G(4x,9(0-0. Ri(t)+e 已提出的算法都存在早熟收敛，易陷入局部最优，缺 式中：M表示施力物j的质量；M表示受力物i的 少有效加速机制. 质量；8是一个小的常量；R,(t)是物体i和物体j之 为了解决以上的不足，本文提出了一种基于万 间的欧几里德距离： 有引力搜索算法的IGSA算法用于求解流水线调度 R(t)=‖X(t),X(t)‖2： 问题.考虑到连续的GSA算法不能处理离散的调度 G(t)是在时间t下的引力常量： 问题，提出了一种最大位置规则.为了提高GSA算 G(t)=Ge吃 法的效率，提出了一种边界变异策略，进而增加种群 则物体i在d维的合力可以表示为 的多样性.并且为了进一步提高解的质量，提出了一 N 种新的局部搜索算法.最后分析了IGSA算法的收 r=∑rand xF(t). i=1同*i 敛性，并证明该算法的空间复杂度为 通过运动法则，在时间t时物体i在第d维的加速度： O((6n+2m)×d)和群体每次进化的最坏渐进时间 F(t) 复杂度为O(md).仿真实验结果表明该算法是有 a(t)=M(t) 效的. 式中：M:(t)表示物体i的惯性质量.则物体的速度 1流水线调度问题的数学模型 更新为 (t+1)rand xv (t)a (t), 流水线调度问题可描述如下：n个待加工的作 x(t+1)=x()+(t+1). 业N=J1,2,…,Jn需要在m台机器加工M=M, 式中：rand是一个在[0,1]之间的随机数，用它可以 M2,·,Mn,每个作业由m道连贯的工序组成，每道 让搜索变得随机化 工序要求不同的机器完成，这些作业通过机器的顺 重力搜索和惯性质量通过适应度函数计算得 序是一样的，它们在每台机器上的顺序也是一样的， 到.质量高的物体吸引力强，移动地比较慢，假设引 每个作业J:在机器m上的处理时间为Pg·对于一 力质量和惯性质量相等，物体的质量可以使用1个 个可行调度π={π1，T2,…,πn},各作业的完工时 隐射.则 间可按如下方法计算： Ma=M=M:=M,i=1,2,…,N, C(π，1)=P1, m,()=m（)-me(t) C(m,1)=C(m-1,1)+P1j=2,3,…,n, met（t)-o(t)' C(π1，i)=C(π1，i-1)+Pmi,i=2,3,…,m, m,(t) M:(t)= C(mj,i)max(C(j-,i),C(mj,i-1))+pm.i, ∑m,(回 j=2,3,…,n,i=2,3,…,m. 式中：mm(t)表示在时刻t,物体i的最好适应度值， 最大完工时间可表示为 met(t)、oe(t)被定义为 Cms（π）=C(πn,m). 流水线调度的目标是发现一个最好的方案π·，使得 m=（)Fenm（), Cm(π)≤C(Ta,m),Vπ∈. ma（）(). 3IGSA调度算法 2 万有引力算法 3.1最大排序规则 万有引力搜索算法9]是基于引力法则，它们质 万有引力搜索算法(GSA)是一种连续的智能算 量的性质对它们之间的行为表现有着一定的作用. 法，标准的万有引力搜索算法所具有的连续编码不 物体之间都是相互吸引的，相互之间的作用力引起 能被直接地用于求解流水线调度.因此构造从物体 物体之间都朝着质量大的物体的方向移动，在GSA 位置矢量到工件排序的恰当映射是应用GSA算法 中，每个物体有4个特征：位置、惯性权重、施力物、 解决流水线调度问题的首要和关键问题.在本文中， 受力物.物体的位置就是问题的解.每个物体被定义 提出一种基于随机键的新的排序规则一最大排序 在一个n维的搜索空间内，由N个物体组成的种群 规则.使用这个规侧，可以将连续的物体位置转化为 X=(（x1,2,…,x),其中第i个物体的位置为X:= 离散的调度方案.在这个规则中，最大的实数将首先 (x,x,…,x,…,x),x代表物体i在d维空间的 被挑选出作为新的调度方案的第1个位置，稍小的 位置. 实数将被挑选出作为新的调度方案的第2个位置

第5期 谷文祥，等：求解流水线调度问题的万有引力搜索算法 .413· 用这种方式，所有物体的位置将被转化为一个新的 体，可以提高优化算法性能.采用如下方式生成： 调度方案，在表1中，使用一个简单的例子来阐述这 xg=(xm-xnta）Xr+xaia 个规则.从表1中，可以很显然地看出1.45是最大 式中：x=0,xm=4.0,r为(0,1)内产生的随机数 的值，所以维数为4对应的调度排序为1.稍小的是 3.4局部搜索算法 1.32,则维数为6对应的调度排序为2.用相同的方 IGSA算法虽然收敛速度比较快，但是它的收敛 法，可以得到它的调度方案为π=（3,4,5,1,6,2). 精度比较低.算法虽然具有比较强的全局搜索能力， 虽然这个方法比较简单，但是它能使得GSA能够求 但它的局部搜索能力较弱，为了提高解的质量，引入 解流水线调度问题. 了2种局部搜索的算子：插人和交换.这样可以有效 表1X的解表示 地避免搜索过程陷入局部极小值，也有利于全局空 Table 1 Solution representation of Agent X 间搜索和局部区域改良能力的平衡. 维数1234 6 交换算子：从1个调度方案挑选出2个不同作 x1.250.850.631.450.231.32 业，并且交换它们的位置 插入算子：从1个调度方案挑选出2个不同作 4516 2 业，将这2个作业之间的作业随着相同的方向移动 3.2边界变异 表1显示的调度方案为π=(3,4,5,1,6,2)，随 在GSA算法的实现过程中，当某个物体在搜索 机选出2个位置2和4，表2显示出执行交换算子所 过程中由于牛顿第二定律（运动定律）的作用使得 得结果，表3显示出执行插入算子所得结果. 物体运动出可行域时，通常的处理方法是使该位置 表2交换算子 处于边界上，即为如下的方法： Table 2 Swap f(x:>xma）then 维数 1 2 3 4 5 6 max x1.251.450.630.850.231.32 End T 3 1 5 If(x;xmr）then 描述 x:=xax-c*rand(·）*xma Procedure local search (z) Begin End Let s,=x permutation of the global solution f(x:<xin）then for i=I to genmax 名：=xin+c*rand(·）*(-xmin) S=5 End f(s)=f(s) 其中：c=0.01,rand为[0,1]之间的一个随机 Find r and r2 randomly and rr if (rand<0.5) 数，从以上的过程可以看出，对越界的物体做了变异 s'=swap (s,r,r) //Swap 操作后，物体不再聚集在边界上，而是分布在离边界 else c×rand附近的可行空间内.通过这种操作，即使物 s'=insert (s,r,r2) //Insert end 体在不可行空间内，克服了使用最大排序规则时产 calculate f(s')//Calculate the makespan 生的排序不惟一问题，同时也增加了物种的多样性。 of the new permutaion 3.3IGSA算法的初始化 if(fs'）-f(s)<=0) 初始物体的位置是GSA搜索的起点.好的初始 S=x' f(s)=f(s') 群体有助于提高解的质量.一个好的初始种群可以 end //end if 保证一定的分布性，这样可以分布覆盖整个解空间. end //end for 从另一方面应包含部分较高质量的个体，以指导算 End 法能搜索到比较好的解.所以，一个高质量的初始群

.414 智能系统学报 第5卷 3.5IGSA算法求解流水线调度问题 在第t次迭代种群对应的调度方案的最大完工时间 图1所示为IGSA求解流水线调度问题的流程 的最小值，π·为调度问题在所有的可能调度方案组 图.从图1中可以看出，一种新的最大排序规则被提 成的集合π中所取的最小值，若π，满足： 出，这种规则可以使连续本质的万有引力算法能直 limP{π，=π}=1， 接用于调度问题.其次，还提出一种边界变异的策略 则称IGSA算法收敛到最优解. 使得越界的物体不再聚集在边界上，而是分布在离 定理1IGSA算法求得的解是有效的. 边界c×rand附近的可行空间内，从而增加种群的 证明结合文献[10]，每种操作都满足“all dif- 多样性.最后，使用一种新的局部搜索算法，局部搜 ferent'”约束，IGSA算法的搜索空间都是由所有有效 索算法可以有效地避免搜索过程陷人局部极小值， 的调度方案构成的，所以IGSA求得的解是有效的. 提高解的质量： 定理2设种群规模为m,问题规模为1，种群 初始化种群 对应的调度状态记为(c1,c2,…,cn),经过若干次迭 使刀最大位置规则计弃每 代后，种群对应的调度状态可以收敛到(c,c,…, 个物体的适应度并找到全 局最优的物体 c*). 证明结合文献[10]，对于改进的万有引力算 终止条件留 Y 输出最优解 法，可以把每个物体看作一个状态，很显然，所有物 TN 更新种群的G、best和worst 体的当前位置可以看作一种状态的分布，由于万有 引力算法是一种随进算法，所以这种状态是会随着 计算每个物休的M和a 算法的运行而发生改变的，算法只与当前的状态有 更新速度和位置，并使川边 关，而与初始状态无关 界变异策路对位置进彳更新 种群对应的调度的状态记为(c1,c2,…,cm),最 使用最大位置规则将每个物 佳调度状态为c·,所有的种群状态构成了一个1× 休的位置转化为调度方案并 N的行向量，其中N=(m×)！,这个行向量的每个 计算：每个物休的适应度 元素由排在一起的实数构成，可表示为 找到全局最优解 {(ci,c,…,ca),(c,c2,…,ca),…,(c,c2,…,c0)}. 经过若干次进化后，已达到最优的种群的状态(c“, 使用局部搜索算法对全局 c·,…,c”),不妨设其排在状态行向量的第1分量 最优解进行进一步提高 处，即 更新全局最优解 {(G,,…,),(c,9…,c),…,(c0,,…,6a) 由物体的速度和位置更新公式可知，算法要将当前 g=g+1 种群中的最优解与前一代保留下来的最优解进行比 较，这一操作用矩阵M来表示，那么从种群第t次 图1IGSA求解流水线调度问题的流程图 迭代C到C+的转移概率为 Fig.1 The framework of the proposed algorithm IGSA P(C=sC=si)= 4算法分析 min{fC),i=1,2,…,m}=f(C*), C=C1; 在基于群体的优化模型中，最优解往往是可以 0. 其他. 预先知道的，本节将讨论利用IGSA算法解决流水 从而矩阵M每一行有且仅有一个1.个体要么被 线调度问题的收敛性问题.收敛性通常是指一个系 替代，要么不变因此，更新矩阵可写为下三角的形式： 统或过程达到一个稳定状态，对基于智能的优化算 法来说，算法的收敛可以根据群体的行为来定义， [MoaA 定义1若IGSA算法在t时刻或者在第t次迭 M= M2.1M2.2 (1) 代种群对应的调度π(t)满足 limπ(t)=r(0),π(0)∈π， LM,lM2…M 那么就称IGSA算法具有渐进收敛性. 式中：Muw为k×k维，而M1是一个单位阵.将式 定义2设IGSA算法的π，是指在t时刻或者 (1)转化为

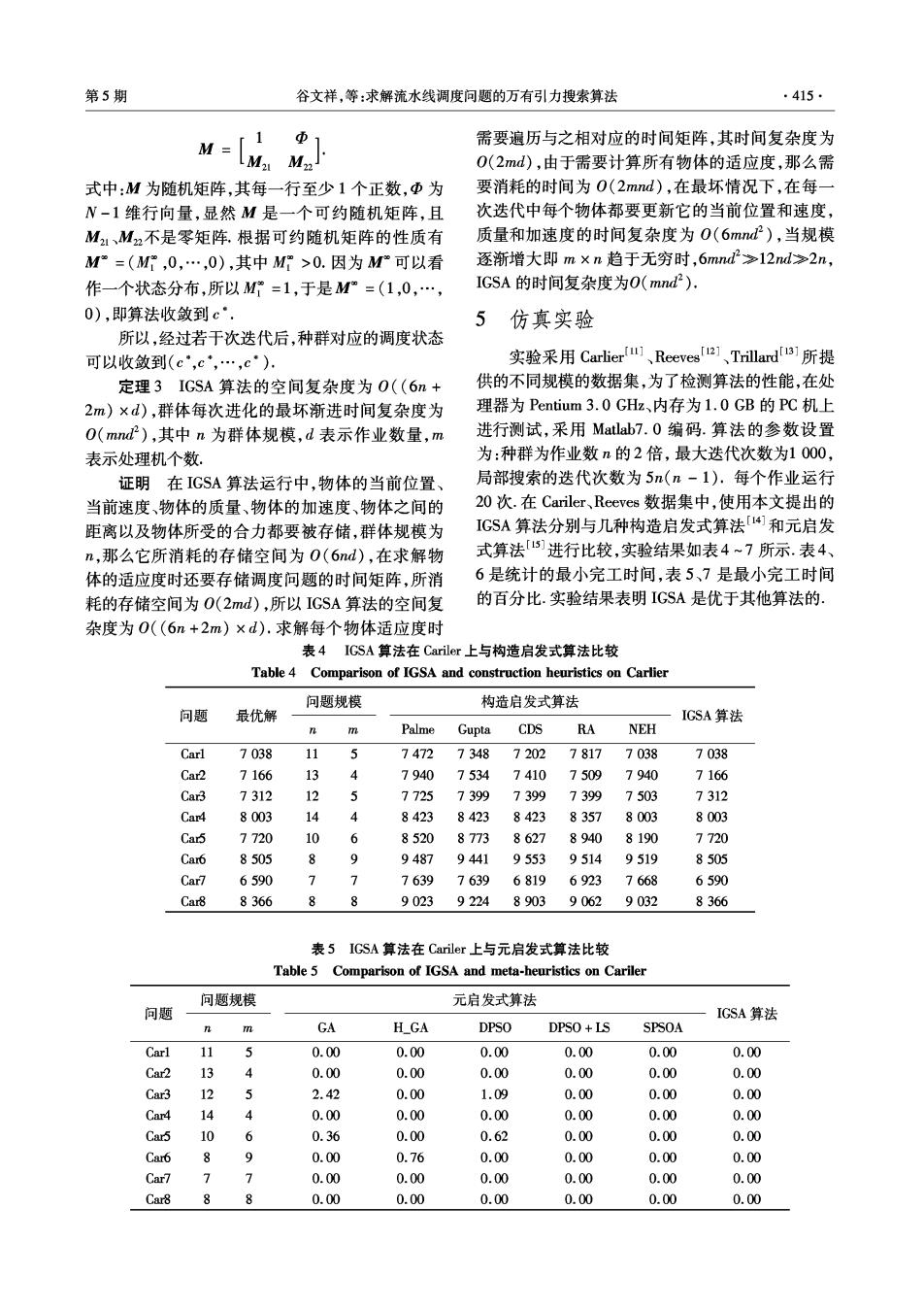
第5期 谷文祥，等：求解流水线调度问题的万有引力搜索算法 ·415 M- 「1 需要遍历与之相对应的时间矩阵，其时间复杂度为 0(2md),由于需要计算所有物体的适应度，那么需 式中：M为随机矩阵，其每一行至少1个正数，更为 要消耗的时间为0(2mnd),在最坏情况下，在每一 N-1维行向量，显然M是一个可约随机矩阵，且 次迭代中每个物体都要更新它的当前位置和速度， M21、M2不是零矩阵，根据可约随机矩阵的性质有 质量和加速度的时间复杂度为O(6mnd2),当规模 M=(M,0,…,0),其中M>0.因为M°可以看 逐渐增大即m×n趋于无穷时，6mnd≥12nd≥2n, 作一个状态分布，所以M=1,于是M=(1,0,…, IGSA的时间复杂度为O(mnd2). 0),即算法收敛到c 5 仿真实验 所以，经过若干次迭代后，种群对应的调度状态 可以收敛到(c‘,c,…,c). 实验采用Carlier、Reeves、Trillard1所提 定理3IGSA算法的空间复杂度为O((6n+ 供的不同规模的数据集，为了检测算法的性能，在处 2m)×d),群体每次进化的最坏渐进时间复杂度为 理器为Pentium3.0GHz、内存为l.0GB的PC机上 O(mnd2),其中n为群体规模，d表示作业数量，m 进行测试，采用Matlab7.0编码.算法的参数设置 表示处理机个数。 为：种群为作业数n的2倍，最大迭代次数为1000， 证明在IGSA算法运行中，物体的当前位置、 局部搜索的迭代次数为5n(n-1).每个作业运行 当前速度、物体的质量、物体的加速度、物体之间的 20次.在Cariler、Reeves数据集中，使用本文提出的 距离以及物体所受的合力都要被存储，群体规模为 IGSA算法分别与几种构造启发式算法[]和元启发 n,那么它所消耗的存储空间为0(6nd),在求解物 式算法「51进行比较，实验结果如表4~7所示.表4、 体的适应度时还要存储调度问题的时间矩阵，所消 6是统计的最小完工时间，表5、7是最小完工时间 耗的存储空间为O(2md),所以IGSA算法的空间复 的百分比.实验结果表明IGSA是优于其他算法的. 杂度为0((6n+2m)×d).求解每个物体适应度时 表4IGSA算法在Cariler上与构造启发式算法比较 Table 4 Comparison of IGSA and construction heuristics on Carlier 问题规模 构造启发式算法 问题 最优解 IGSA算法 0 Palme Gupta CDS RA NEH Carl 7038 11 5 7472 7348 7202 7817 7038 7038 Car2 7166 13 4 7940 7534 7410 7509 7940 7166 Car3 7312 12 J 7725 7399 7399 7399 7503 7312 Car4 8003 14 o 8423 8423 8423 8357 8003 8003 Car5 7720 10 8520 8773 8627 8940 8190 7720 Car6 8505 8 9 9487 9441 9553 9514 9519 8505 Car7 6590 7 7 7639 7639 6819 6923 7668 6590 Car8 8366 8 8 90239224 89039062 9032 8366 表5IGSA算法在Cariler上与元启发式算法比较 Table 5 Comparison of IGSA and meta-heuristics on Cariler 问题规模 元启发式算法 问题 IGSA算法 m GA H_GA DPSO DPSO +LS SPSOA Carl 11 5 0.00 0.00 0.00 0.00 0.00 0.00 Car2 13 0.00 0.00 0.00 0.00 0.00 0.00 Car3 12 2.42 0.00 1.09 0.00 0.00 0.00 Car4 14 4 0.00 0.00 0.00 0.00 0.00 0.00 Car5 10 6 0.36 0.00 0.62 0.00 0.00 0.00 Car6 0 0.00 0.76 0.00 0.00 0.00 0.00 Car7 0.00 0.00 0.00 0.00 0.00 0.00 Car8 8 8 0.00 0.00 0.00 0.00 0.00 0.00

416 智能系统学报 第5卷 表6IGSA算法在Reeves上与构造启发式算法比较 Table 6 Comparison of IGSA and construction heuristics on Reeves 问题规模 构造启发式算法 问题 最优解 IGSA算法 n Palme Gupta CDS RA NEH Rec01 1247 20 1391 14341399 1399 1334 1247 Rec03 1109 20 5 1223 1380 1273 1159 1136 1109 Rec05 1242 20 5 1290 1429 1338 1434 1294 1245 Rec07 1566 20 10 1715 16781697 1722 1637 1566 Rec09 1537 20 10 1915 1792 16391714 1692 1537 Recl1 1431 20 10 16851765 1597 16361635 1431 表7IGSA算法在Reeves上与元启发式算法比较 Table 7 Comparison of IGSA and meta-heuristics on Reeves 问题规模 元启发式算法 问题 IGSA算法 n m GA HGA DPSO DPSO +LS Rec01 20 5 8.26 0.14 1.36 0.16 0.00 Rec03 20 5 7.21 0.09 0.54 0.18 0.00 Rec05 20 5 5.23 0.29 0.97 0.24 0.24 Rec07 20 10 8.56 0.69 3.70 1.15 0.00 Rec09 20 10 5.14 0.64 5.47 2.41 0.13 Rec11 20 0 8.32 1.10 11.11 1.05 0.51 对于Trillard数据集，将本文的IGSA算法与 最大迭代次数依次为：400、400、400、500、2000 Lian提出的NPS0算法81比较，IGSA使用和NPS0 2000、800.实验结果如表8所示. 相同的参数设置，种群个数为50，各个规模的实验 表8IGSA算法与NPS0比较的结果 Table 8 Comparison of IGSA and NPSO 问题规模 NPSO(Lian,et al,2008) IGSA算法 FSSP 最优解 m Min Max Avg Min Max Avg Ta001 20 5 1278 1278 1297 1297.9 1278 1278 1278.0 Ta011 20 10 1582 1582 1639 1605.8 1583 1614 1600.7 Ta021 20 20 2297 2297 2367 2334.9 2297 2356 2331.4 Ta031 50 5 2724 2724 2729 2425.0 2724 2724 2724.0 Ta041 50 10 2991 3034 3129 3086.9 3025 3046 3032.2 Ta051 50 20 3771-3847 3938 3989 3964.3 3933 3952 3940.7 Ta061 100 5 5493 5493 5495 5493.0 5493 5493 5493.0 表8表明在求解调度问题时IGSA算法明显优 1.60×10 于NPs0算法，从表中可以看出除了TanO11的最小 一最优解 1.55 值，IGSA算法不能发现最优解，对于另外的数据集， ,最优解平均值 1.50 IGSA算法都能提供比较好的最小值、最大值和平均 1.45 值.图2显示了不同规模数据的IGSA算法的收敛 1.40 曲线以及最优解平均值的收敛曲线，从图中看出， 1.35 IGSA算法能很快地收敛到最优解，说明该算法的收 1.30 敛性比较好，同时也证明了局部搜索的有效性。 1.25 0 ×10 3 迭代次数 (a)Tan001

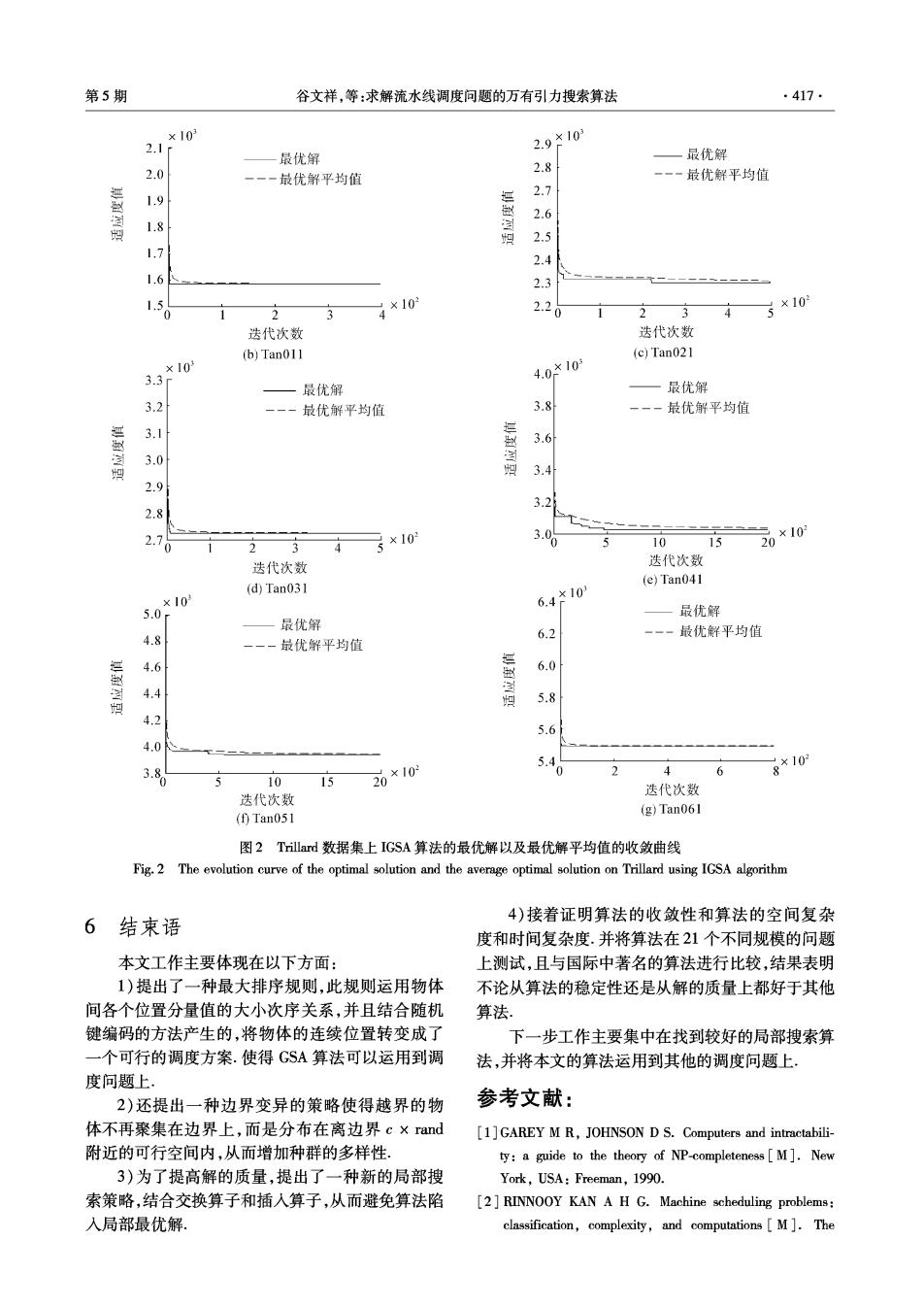
第5期 谷文祥，等：求解流水线调度问题的万有引力搜索算法 .417 10 2.1f 2.9×10 一最优解 ,最优解 2.0 2.8 最优解平均值 一一一最优解平均值 1.9 2.7 2.6 1.8 2.5 1.7 2.4 1.6 2.3 1.5 2 3 ×10 4 2.20 2 3 ×10 迭代次数 迭代次数 (b)Tan011 (c)Tan021 ×10 3.3 4.0*10 最优解 最优解 3.2 最优解平均值 3.8 -一一最优解平均值 3.1 3.6 3.0 3.4 2.9 3.2 2.8 2.10 ×10 3.0 10 20*10 迭代次数 迭代次数 (d)Tan031 (e)Tan041 0*0 6.4*10 最优解 最优解 4.8 最优解平均值 6.2 最优解平均值 4.6 到 6.0 4.4 5.8 4.2 5.6 4.0 3.8 20*10 5.40 2 6 8*10 5 10 15 迭代次数 迭代次数 (f)Tan051 (g)Tan061 图2 Trillard数据集上IGSA算法的最优解以及最优解平均值的收敛曲线 Fig.2 The evolution curve of the optimal solution and the average optimal solution on Trillard using IGSA algorithm 6结束语 4)接着证明算法的收敛性和算法的空间复杂 度和时间复杂度.并将算法在21个不同规模的问题 本文工作主要体现在以下方面： 上测试，且与国际中著名的算法进行比较，结果表明 1)提出了一种最大排序规则，此规则运用物体 不论从算法的稳定性还是从解的质量上都好于其他 间各个位置分量值的大小次序关系，并且结合随机 算法 键编码的方法产生的，将物体的连续位置转变成了 下一步工作主要集中在找到较好的局部搜索算 一个可行的调度方案.使得GSA算法可以运用到调 法，并将本文的算法运用到其他的调度问题上. 度问题上 2)还提出一种边界变异的策略使得越界的物 参考文献： 体不再聚集在边界上，而是分布在离边界c×rand [1]GAREY M R,JOHNSON D S.Computers and intractabili- 附近的可行空间内，从而增加种群的多样性， ty:a guide to the theory of NP-completeness [M].New 3)为了提高解的质量，提出了一种新的局部搜 York,USA:Freeman,1990. 索策略，结合交换算子和插入算子，从而避免算法陷 [2]RINNOOY KAN A H G.Machine scheduling problems: 入局部最优解。 classification,complexity,and computations[M].The

·418. 智能系统学报 第5卷 Hague,The Netherlands:Nijhoff,1976. [12]REEVES C R,YAMADA T.Genetic algorithms,path re- [3]CROCE F D,NARAYAN V,TADEI R.The two-machine linking and the flowshop sequencing problem[J].Evolu- total completion time flow shop problem[J].European Jour- tionary Computation,1998,6(1):45-60. nal of Operational Research,1996,90:227-237. [13]TAILLARD E.Benchmarks for basic scheduling problems 4]CROCE F D,GHIRARDI M,TADEI R.An improved [J].European Joural of Operational Research,1993, branch-and-bound algorithm for the two machine total com- 64:278-285. pletion time flow shop problem[J].European Journal of [14]PONNAMBALAM S G,ARAVINDAN P,CHANDRASEK- Operational Research,2002,139:293-301. ARAN S.Constructive and improvement flow shop schedu- [5]PALMER D S.Sequencing jobs through a multistage process ling heuristics:an extensive evaluation J].Production in the minimum total time:a quick method of obtaining a Planning Control,2001,12(4):335-344. near-optimum[J].Operational Research Quarterly,1965, [15]WANG L.ZHENG D Z.An effective hybrid heuristic for 16:101-107. flowshop scheduling[J].International Journal of Advanced [6]GUPTA J N D.Heuristic algorithms for multistage flowshop Manufacturing Technology,2003,21:38-44. scheduling problem[J].AIlE Transactions,1972,4:11- 作者简介： 18. 谷文样，男，1947年生，教授、博士 [7]KUO Ihong,HORNG Shijinn,KAO Tzongwann,et al.An 生导师，主要研究方向为智能规划与规 efficient flow-shop scheduling algorithm based on a hybrid 划识别、形式语言与自动机、模糊数学 particle swarm optimization model[J].Lecture Notes in 及其应用.参加或承担国家自然科学基 Computer Science,2007,4570:303-312. 金、教育部重点项目、省科委项目多项， []LIAN Zhigang,GU Xingsheng,JIAO Bin.A novel particle 发表学术论文100余篇， swarm optimization algorithm for permutation flow-shop scheduling to minimize makespan[J].Chaos,Solitons and 李向涛，男，1987年生，硕士研究 Fractals,2008,35:851-861. 生，主要研究方向为智能规划、智能信 [9]RASHEDI E,NEZAMABADI-POUR H,SARYAZDI S. 息处理 GSA:a gravitational search algorithm[J].Information Sci- ence,2009,179(13):2232-2248. [10]张长胜，孙吉贵，欧阳丹彤，等.求解车间调度问题的自 适应混合粒子群算法[J].计算机学报，2009,32(11)： 2137-2146, 朱磊，男，1987年生，硕士研究 ZHANG Changsheng,SUN Jigui,OUYANG Dantong,et 生，主要研究方向为智能规划、智能信 al.A self-adaptive hybrid particle swarm optimization algo- 息处理。 rithm for flow shop scheduling problem[J].Chinese Jour- nal of Computers,2009,32(11):21372146. [11]CARLIER J.Ordonnancements a contraintes disjonctives [J].RAIRO Recherche Operationelle,1978,12:333- 351