
第5卷第4期 智能系统学报 Vol.5 No.4 2010年8月 CAAI Transactions on Intelligent Systems Aug.2010 doi:10.3969/j.issn.1673-4785.2010.04.008 不确定非线性时滞系统的自适应滑模控制 罗小元,朱志浩,关新平 (燕山大学电气工程学院,河北秦皇岛066004) 摘要:针对一类不确定非线性时滞系统的鲁棒滑模控制器设计问题,提出了一种自适应滑模控制方法,该方法能 够有效地削弱系统的输入抖动.基于自适应滑模控制技术和Lyapunov稳定方法,克服了系统不确定性和时滯特性影 响,不但保证系统状态可以在有限的时间内到达滑模面,而且还保证了系统的渐近稳定特性.最后给出的仿真结果 验证了该控制方案的有效性. 关键词:非线性时滞系统;自适应控制;滑模控制 中图分类号:TP273文献标识码:A文章编号:16734785(2010)040332-04 Adaptive sliding mode control for uncertain nonlinear time-delay systems LUO Xiao-yuan,ZHU Zhi-hao,GUAN Xin-ping (College of Electrical Engineering,Yanshan University,Qinhuangdao,qinhuangdao 066004,China) Abstract:Problems occur when robust sliding model controller designs are applied in uncertain nonlinear time-delay systems.To resolve them,an adaptive sliding mode controller which effectively reduced input chattering was pro- posed.With the sliding controller technique and the Lyapunov stability method,the influence of both uncertainty and time-delays on the system was considerably reduced.Furthermore,system states reached a sliding mode plane within a finite time,with asymptotical stability guaranteed.The simulation results demonstrated the validity of the proposed approach. Keywords:nonlinear systems;adaptive control;sliding model control 在实际工程系统中,时滯经常是不可避免的,时独立于参数不确定性和外界干扰,故SMC在此类情 滞的存在使系统丧失了许多性质,甚至稳定性.因 况下起到了较好的控制性能,除此之外,在坦克炮控 此,时滯系统的鲁棒控制得到了广泛关注.近年 伺服系统、航空气动伺服控制系统、电机-泵组控制 来,滑模控制(sliding mode control.,SMC)已得到深 系统等实际场合中也得到了广泛应用.因此,SMC 入研究,并被广泛应用于工业控制系统中2],例如: 已成为一种强有力的鲁棒控制方法。 大跨距双起升轨道式集装箱龙门起重机(双起升场 尽管如此,系统输入抖动仍是滑模控制实际应 桥)由于存在不同箱重、不同提升速率以及驱动电 用中的主要障碍.通常利用较大的控制增益来处理 机特性等差异,其吊具机构在运动过程中会出现两 未知参数的变化和外界干扰,但它会增加输入抖动 吊具之间的动态与静态偏差,从而影响双吊具系统 和导致系统的不稳定性,与此同时,边界层技术34 的装卸效率,双吊具运动的同步协调控制是提高其 和自适应参数辨识机理6是削弱系统输入抖动的 装卸效率的重要因素.在匹配条件下由于滑模控制 普遍方法.现有的文献已验证边界层宽度可变的 SMC比固定宽度的SMC具有更好的跟踪性能.文献 收稿日期:200906-11. [7]提出了边界层宽度与控制增益自适应方法.文 基金项目:国家自然科学基金资助项目(60525303,60704009):燕山 献[8-10]提出了调整边界层宽度的模糊算法.但上 大学博士基金资助项目(B209). 通信作者:罗小元.E-mai:yluo@ysu.ed.cm 述文献中都未同时考虑不确定性和时滞特性对系统

第4期 罗小元,等:不确定非线性时滞系统的自适应滑模控制 ·333· 的影响。 抖动问题,但是固定的控制增益与边界层宽度会导 本文利用鲁棒自适应滑模控制和Lyapunov稳 致跟踪精度降低.因此,本文利用自适应方法来克服 定方法,研究了一类更广泛的不确定非线性时滞系 系统控制输入抖动问题的同时又能保证准确跟踪误 统的滑模控制问题,利用自适应滑模控制技术克服 差的思想是非常有意义的. 了系统不确定性和时滞特性的影响,确保系统在有 假定系统(1)采用设定值控制,令xa=0;如果 限的时间内可以到达滑模面.最后通过仿真验证了 式(4)成立,那么最终会使S→0和e0.在此条件 所提出的控制方法的有效性。 下,系统的自适应滑模控制律“可以描述为 u=-(c"b)(c"fo (x)+ 1系统描述 c"go(x(t-d))+Ad(a,S)). (5) 考虑一类具有不确定性和时滞特性的非线性系 式中:自适应参数入和α分别是控制增益参数和边 统,此系统用如下方程描述 界层参数,中(α,S)是一个S形函数,形式如下: x=f(x(t))+g(x(t-d))+bu, a.》=器二8 (6) x(t)=p(t),t∈[-d,0], (1) y=x1: 显而易见,参数α决定了连续函数中(α,S)的 式中:x=[x12…xn]T=[x1龙…x-》]T∈R是状 宽度,通过调整边界层参数和控制增益可以使跟踪 态矢量,u∈R"是控制输入向量,f(x)∈R"和 误差e0,文献[36]已验证边界层技术和自适应参 g(x(t-d))R"是时变矢量函数,d是系统定常时 数辨识机理是削弱系统输入抖动的有效方法.因此, 滞,b=[0…01]T初始条件p(t)是t∈[-d,0]上 具备可变的边界层宽度与控制增益的滑模控制器可 以更加有效地削弱输入抖动和消除系统稳态误差, 的连续初始矢量函数.设f(x),g(x(t-d))可以转 化为如下形式 自适应律设计如下: [f(x(t))=f(x(t))+Af(x(t)), d-vebeng)s (7) Lg(x(t-d))=80(x(t-d))+Ag(x(t-d)). (2) f=e}+二a》 (8) 式中:6(x)=[x2…x.6]T分别是f(x)∈R、 式中:y和e是用来调整自适应律的正实数, g(x(t-d)∈R”的标称部分,参数变量△f(x)= 定理1考虑满足条件(2)的不确定非线性时 [0…0△f6]T、△g(x(t-d)=0…0△go]F是有 滯系统(1),给定滑模函数(3),设计控制律(5)、 界可微的. (6),自调整律(7)、(8),则闭环系统(1)渐进稳定, 假定系统的期望状态矢量为xa=[xax2a, 且有效地消除了系统稳态误差, xd]T∈R,跟踪误差定义为e=x1-x1a本文的控制 证明取系统(I)的Lyapunov函数为 目标为使状态x1逼近期望状态x1d,即e0, v-gd. (9) 2滑模控制器设计 对式(9)Lyapunov函数进行求导 采用滑模控制策略,定义滑模函数如下 av ae as日uah+ =V+V:=be ai ou a at S=ce. (3) aV de 0xi au da 式中:c=[c1c2…c.]T,e=[ee…ea-w].,c2, de ax ou da ot …,cn是使cns-1+cn-1s-2+…+c1为Huwitz多项 r-ye0tu以 式的正实数,同时满足cb≠0. aeax1auaλat 控制输人的选择条件是 {-(e'b)'(e(x)+ e 0u0入 SS<0. (4) 边界层技术常用于解决传统滑模控制中存在的 c'8o(x(t-d)+A中(a,S)月队= at
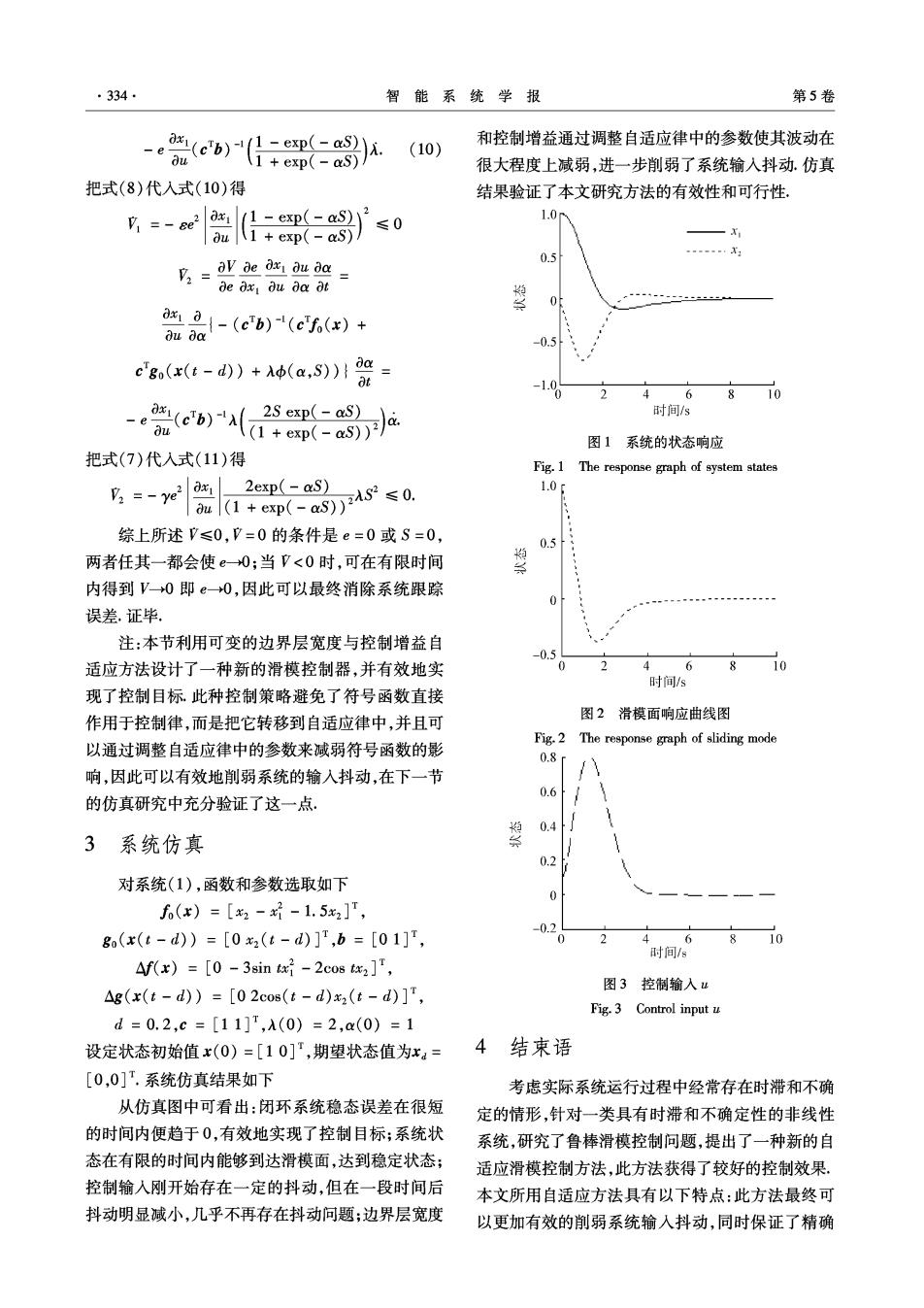
334· 智能系统学报 第5卷 -e (c"b) -exp(-aS)). 和控制增益通过调整自适应律中的参数使其波动在 (10) du 1 exp(-aS) 很大程度上减弱,进一步削弱了系统输入抖动.仿真 把式(8)代入式(10)得 结果验证了本文研究方法的有效性和可行性。 V=-se Oz (1-exp(-as)2 1.0 ≤0 au1 exp(-aS) -X V:av e 0ax au aa 0.5 ---X2 de ox ou da ot a0{-(c'b)(cf(x)+ du dx -0.5 c'go(x(t-d))+d(a.S)) t 1% 46810 -0e62{a 时间/s 图1系统的状态响应 把式(7)代入式(11)得 Fig.1 The response graph of system states 男-aa0 1.0c 综上所述V≤0,V=0的条件是e=0或S=0, 两者任其一都会使e0;当7<0时,可在有限时间 内得到V→0即e0,因此可以最终消除系统跟踪 误差,证毕 注:本节利用可变的边界层宽度与控制增益自 -0.5 适应方法设计了一种新的滑模控制器,并有效地实 0 4 6810 时间/s 现了控制目标此种控制策略避免了符号函数直接 作用于控制律,而是把它转移到自适应律中,并且可 图2滑模面响应曲线图 以通过调整自适应律中的参数来减弱符号函数的影 Fig.2 The response graph of sliding mode 0.8r 响,因此可以有效地削弱系统的输入抖动,在下一节 的仿真研究中充分验证了这一点. 0.4/ 3系统仿真 0.2 对系统(1),函数和参数选取如下 0 f6(x)=[x2--1.5x2]T, -0.2 go(x(t-d))=[0x2(6-d)]T,b=[01]T, 0 4 810 时间s Af(x)=[0-3sin ti-2cos tx2 ] Ag(x(t-d))=[02cos(t-d)x2(t-d)]", 图3控制输入u Fig.3 Control input u d=0.2,c=[11]T,A(0)=2,x(0)=1 设定状态初始值x(0)=[10],期望状态值为xa= 4结束语 [0,0]'.系统仿真结果如下 考虑实际系统运行过程中经常存在时滞和不确 从仿真图中可看出:闭环系统稳态误差在很短 定的情形,针对一类具有时滞和不确定性的非线性 的时间内便趋于0,有效地实现了控制目标;系统状 系统,研究了鲁棒滑模控制问题,提出了一种新的自 态在有限的时间内能够到达滑模面,达到稳定状态; 适应滑模控制方法,此方法获得了较好的控制效果 控制输入刚开始存在一定的抖动,但在一段时间后 本文所用自适应方法具有以下特点:此方法最终可 抖动明显减小,几乎不再存在抖动问题;边界层宽度 以更加有效的削弱系统输入抖动,同时保证了精确

第4期 罗小元,等:不确定非线性时滞系统的自适应滑模控制 ·335· 的的误差跟踪性能,并且使得边界层宽度和控制增 parameters[J].IEEE Transactions on Fuzzy Systems, 益很快趋于它们的最终值,最后给出的仿真结果验 Man,and Cyberetics,2001,9(2):343-348. 证了该方法的有效性 [9]LEE H,KIM E,KANG H J,PARK M.A new sliding- mode control with fuzzy boundary layer[J].Fuzzy Sets and 参考文献: Systems,2001,120(1):135-143. [10]KUO T C,HUANG Y J,CHANG S H.Sliding mode con- [1]GU K,NICULESCU S I.Further remarks on additional dy- namics in various model transformations of linear delay sys- trol with self-tuning law for uncertain nonlinear systems [J].1 SA Transactions,2008,47(2):171-178. tems[J].IEEE Trans Autom Contr,2001,46(3):497- 作者简介: 500. 罗小元,男,1976年生,副教授,博 [2]HUANG Y J,KUO T C.Robust output tracking control for 士,主要研究方向为鲁棒控制、非线性 nonlinear time-varying robotic manipulators[J].Electrical 控制、多智能体协调控制等。主持和参 Engineering,2005,87(1):47-55. [3]SLOTINE J-JE,LI W.Applied nonlinear control[M].En- 与国家自然基金4项、省部级基金3 glewood Cliffs(NJ):Prentice-Hall,1991:21-25. 项,发表论文30余篇. [4]HUANG Y J,KUO TC.Robust position control of DC ser- vomechanism with output measurement noise[J].Electrical 朱志浩,男,1984年生,硕士研究 Engineering,2006,88(3):223-338. 生,主要研究方向为非线性控制,参与 [5]FURUTA K.VSS type self-tuning control[J].IEEE Trans- 国家自然科学基金1项,发表论文3 actions on Industrial Electronics,1993,40(1):37-44. 篇。 [6]LEE P M,OH J H.Improvements on VSS type self-tuning control for a tracking controller[J].IEEE Transactions on Industrial Electronics,1998.45(2):319-325. [7]CHANG W D,HWANG R C,HSIEH J G.Application of 关新平,男,1963年生,教授,博士 an auto-tuning neuron to sliding mode control[J].IEEE 生导师,主要研究方向为非线性控制、 Transactions on Systems,Man,and Cybernetics,2002,32 鲁棒控制、网络控制系统,无线网络及 (4):517-529. [8]LHEE C G,PARK J S,AHN H S,KIM D H.Sliding 应用等.主持国家自然基金3项,省部 mode-like fuzzy logic control with self-tuning the dead zone 级项目4项.发表论文160余篇