
第5卷第5期 智能系统学报 Vol.5 No.5 2010年10月 CAAI Transactions on Intelligent Systems 0ct.2010 doi:10.3969/i.issn.1673-4785.2010.05.005 手写运动的协作基元合成分析方法 刘敏,王国利 (中山大学信息科学与技术学院,广东广州510006) 摘要:研究一种生物运动神经控制机理与数据合成分析相结合的手写运动分析方法.特别地,将运动协作基元的 概念用于手写运动数据分析,研究手写运动的协作基元合成分析方法,建立符合生物运动神经控制规律的手写运动 数据理解模式.提出的协作基元合成分析过程由2个交替迭代的优化算法组成:其一,基于非负矩阵因子分解模式 估计协作基元及调制幅度;其二,采用相似性最大化准则估计协作基元的激活时间.针对笔画切分的实验研究表明, 采用协作基元合成分析方法获得的笔画切分结果,能够很好揭示相邻笔画之间的重叠连接模式,证实了所提方法的 有效性. 关键词:手写运动;运动基元;合成分析;非负矩阵分解;生物运动神经控制;相似最大化准则 中图分类号:1P39文献标识码:A文章编号:1673-4785(2010)05040506 Handwriting movement analysis by synthesis of synergic primitives LIU Min,WANG Guo-li (School of Information Science and Technology,Sun Yat-sen University,Guangzhou 510006,China) Abstract:A novel methodology of handwriting analysis was explored in relation to the biological motor control hy- pothesis and the data analysis by a synthetic approach.In particular,the main concern was the issue of handwriting data analysis with movement primitives,in which the analysis by a synthetic approach was presented to build a data understanding paradigm that respects the synergic hypothesis of the biological motor control.The proposed synthetic analysis approach was comprised of two alternately iterative optimization algorithms;the non-negative matrix factori- zation paradigm was applied for primitive decompositions while the correlative maximization principle was employed for estimating activation time of synergic primitive.The experimental studies for stroke segmentation obtained by the synthesis of synergic primitives validate the proposed method by showing that the superposed connection mode of neighboring strokes can be recognized from handwriting data. Keywords:handwriting movement;movement primitives;synthetic analysis;non-negative matrix factorization;bio- logical motor control;correlative maximization principle 揭示生物运动神经控制的计算机制是运动行为 成计算模型的数据表示和数据处理方法。 分析的重要内容山,在运动神经认知21、仿生机器 运动神经控制协作是生物运动神经认知和神经 人)、运动神经疾病诊疗和康复4们、人机交互界面 计算领域的核心概念和研究基础),在认识和分析 设计5]等领域有重要的应用.手写运动分析是神经 运动神经控制机理方面发挥着重要作用.协作基元假 计算等研究领域最受关注的研究热点[6],其中揭示 说认为,复杂的运动神经控制过程都可以看成是由若 手写运动生成规律所涉及的数据表示和数据处理方 干简单的基本运动神经控制模式(即运动基元)混合 法的研究已引起广泛关注9.本文采用合成分析 叠加的结果.将协作基元假说引入到获取手写运 的模式,研究从观测的手写数据中获取手写运动生 动生成计算模型的数据表示和数据处理方法中,特别 地,采用协作基元卷积混叠的手写数据表示形式,给 收稿日期:2009-12-10. 出了协作基元合成分析的手写数据处理方法. 基金项目:国家自然科学基金资助项目(60775055). 通信作者:王国利.E-mail:isswgl@mail.sysu.ed血.cm 本文研究的主要贡献包括:1)将生物运动神经

·406 智能系统学报 第5卷 控制协作机理与手写运动数据合成分析方法结合, Y轴的分量.给定笔端初始位置po=[x0yo]I,一次 建立了协作基元合成分析模型、较动力学模型] 连续的笔端运动轨迹p(t)=[x(t)y(t)]T可以表 微分几何模型、运动学模型]等手写分析方法, 示为 它依赖和受限于特定模型机理的适应范围,具有更 「x(t) 普遍的适用性;2)在手写数据协作基元合成分析过 =+.()dr, (2) 程中,引入协作基元激活时间参量,强调协作基元的 ()=为+,(r)dr 异步特性,是对已有同步控制协作基元混合表示模 注解2在平面速度域上,依据生物运动神经 型4的发展;3)提出的手写运动合成分析方法,在 协作基元假说,协作基元:(t)对手写运动的贡献 功能上实现了手写运动过程由复杂到简单的分解, 较已有的基于时间或空间的笔画切割策略],允许 是以波形向量作为整体参与的,即w:()一旦被激 活将执行整个过程.特别地,可以将":(t)理解为特 手写运动协作基元在时间和空间上发生重叠,更符 合生物运动神经控制规律16] 定笔划单元的运动生成模板,其起始和终止状态自 然约束为零.需要指出的是,在时间轴上允许不同的 1问题描述及方法概述 协作基元发生重叠和交叉,对应笔画的光滑连接。 注解3序列{T:,c:}可以理解为实现手写运动 本文提出的手写运动数据合成分析方法涉及以 的指令参数,在T:时刻激活并以幅值c:调制:(t) 下2个关键环节.首先,需要表示出手写运动数据的 的控制输入可以描述为c(t)=c,6(t-T:),对应的 合成分析模型.其次在此基础上,建立手写数据合成 分析的实现算法.其中,生物运动协作基元假说是本 输出响应(c⑧*w:)(t)为w:(t)对手写运动的贡 文手写运动数据合成分析方法的基础0 献.如图1所示,式(1)可以等价地表示成如下卷积 如前所述,大量的生物神经运动生理学实验证 叠加形式: 据表明,运动神经中枢是在速度域上组织实施手写 m(t)= (c*w)(t) (3) 运动协作基元的调制和合成过程?,.本文在手写 数据合成分析的过程中将以此为基础,建立手写数 c() () 据的协作基元表示模型.特别地,将观测的手写运动 c"w:(t-7) 在速度域上表示成向量m(:),将手写运动协作基元 c2(t) cw(t-t》 w() 模型化为一组向量波形函数{w:(t)1,则手写运 动的发生过程可以模型化为 cwk-》 e""(t w(0 m(t)=】 ∑cw(t-T). (1) 图1手写运动数据表示模型 式中:T:和c:分别为第i个协作基元的激活时间和 Fig.1 Data represent model for handwriting movement 调制幅度,从数据分析的角度,式(1)右端可以看作 综合注解1和2,作以下合理的约定: 是对左端观测手写数据的解释;从数据合成的角度, 假设1m(t)的支集supp(m(t))覆盖w:(t- 式(1)右端给出了协作基元合成手写数据的模型. T)的支集supp(w:(t-T:),且 将手写运动数据合成分析的任务描述成: supp(m(t))=U supp(wi(t-T;)). 问题1对于给定观测数据m(t),如何获得式 当控制指令c0(t)形式上退化为c0(t)= (1)右端的数据表示? ℃:6(t)时,即假定所有协作基元w:(t)以同步的方式 上述问题可以归结为协作基元w:(t)的提取, 以及激活时间r:和调制幅度c:的估计问题。 发生,则问题1可以简化为波形分析问题1.然而, 注解1本文关注通过数位板获取的手写运动 在手写运动生成过程中,协作基元是以非同步方式 数据,将笔端运动速率作为观测数据m(t),即 发生的,激活时间{T:}具有重要的生物运动神经控 制意义,因此问题1可以看成是参数化的波形分析 m(t)= 「(t)1 L,(t) 问题.由于激活时间{T:}同样是待定的参数,已有的 波形分析方法不再适用,这也是解决问题1面临的 式中:v(t)和v,()分别为笔端运动速率在X轴和 新的技术难点.为此,将问题1分解成2个子问题:

第5期 刘敏,等:手写运动的协作基元合成分析方法 ·407· 问题2已知激活时间{T:}的情形下,确定协 式中:0为全零的列向量,e。表示仅有第k个元素为 作基元{w:(t)}和调制幅度{c:}. 1其余为零的T维列向量.结合式(6)~(8),得到 问题3已知协作基元{w:(t)}和调制幅度 WH=W⊙ (9) {c}的情形下,估计激活时间{r:. 式中:H为第i个波形的调制结构矩阵,定义为 本文求解问题1的基本思路是:采用交替迭代 H:=[0…0⊙0…0]r (10) -1 N-i 计算模式组织上述2个子问题的求解过程,进而间 式中:0是T×T方阵,综合式(1)、(4)、(5)、(7)和 接实现问题1的求解.特别地,在每一轮迭代过程 (9),得到矩阵因子分解的表示形式: 中,问题2的求解环节将以上一轮问题3的求解结 M=WH. (11) 果作为激活时间{τ:}的估计值,问题3的求解环节 则以此轮问题2的结果作为协作基元{w:(t)}和调 式中:H=1cH 注解4式(11)给出了手写运动数据的结构化 制幅度{c}的估计,由此形成问题1的交替迭代求 因子分解表示形式,其中调制结构矩阵H,完全由 解过程.不难看出,寻找问题2和问题3的求解方法 激活时间T:确定,是对矩阵因子H的结构约束 成为解决问题1的关键,是本文的主要研究内容.需 要指出的是,在问题2中,尽管激活时间{T:}已知, 至此,问题2的求解可以归结为如下带结构约 束的矩阵因子分解问题, 但考虑到协作基元的异步发生方式以及非负约束特 问题4对于数据矩阵M以及结构约束矩阵 性,仍然是求解问题1的难点问题.下一节将详细讨 {H},确定和e=[c1c2…cw]T使得 论实现问题2和问题3的求解方法. (w,c)arg minJ(W,c)=: W.c 2主要结果 M-w∑aI, 如上节所述,解决问题1的关键技术环节是寻 [W]前≥0,c≥0,Vij,k. (12) 找问题2和问题3的求解方法,即协作基元分解和 式中:IAIp=tr(ATA)n=(∑)为Frobenius 激活时间参数估计的方法,这是本节重点讨论的内 范数,[A]u表示矩阵A中(k,)处的元素, 容.首先建立协作基元分解的实现方法,然后给出激 注解5对于按式(4)构造的手写数据矩阵M, 活时间的估计策略, 一旦获得问题4的解巾,则按式(5)和(6)可直接提 2.1手写运动协作基元的分解 取出手写运动基元波形的离散序列{W:(). 考虑采用数位板获取的手写运动的离散采样数 注解6问题4的优化目标可以理解为极小化 据{m()j=1,2,…,T.本文拟在式(1)或式(3)的 合成分析模型(1)重构观测手写数据的二次残差. 基础上,将手写数据表示为因子分解的形式,进而能 注意到手写运动协作基元是描述手写运动在X轴 够利用因子分解的手段实现协作基元的波形分解。为 和Y轴速率分量的发生过程.为此,在问题4中引入 此,按如下方式构造手写运动观测数据矩阵M: 非负约束,以排除不合理的运动协作基元分解模式 M=col{m(t),m(t2),…,m(tr)}.(4) 不难发现,问题4面临着与无结构约束的非负 式中:col{1,”2,…,"m}表示由向量序列{y}按列排 矩阵因子分解相同的挑战,即目标函数J(W,c)关 成的矩阵,换言之,矩阵M的第j列为手写运动的 于(W,c)是非凸的.但同样可以借助J(W,c)分别 第j个观测样本m(),对应第个协作基元w:(t). 关于W和c的凸性,将问题4的求解问题分解为交 定义波形矩阵: 替迭代的2个凸优化过程.以下将结合梯度速降的 W=col{w:(t1),w:(t2),…,w:(tr)} (5) 迭代策略建立问题4的交替迭代求解算法, 进一步定义: 分别计算J(W,c)关于W和c的梯度,得到 W=[W1W2·Ww]. (6) 不失一般性,以下将激活时间x:理解为,其中1≤ =-2(MF-w阳H). l,≤l≤T,1≤i≤'≤N.注意到: al =-2u(MW.-HWWe.). W8=col{00,w:(t),…,w(tr-){.(7) 0c: 则求解问题4对应的增量迭代规律可以表示成: 式中:®是T×T方阵,且 []a←-[m]u+6u[M-War]a,(13) ⑨,=col{0,-0,e1,…,er- (8) c:+c+n:tr(MWe -Awwe )(14)

·408 智能系统学报 第5卷 式中:δu和n:是迭代步长因子.为了保证非负约束 式(18)导出的.因此,可以通过对r:(?)在Y:上的 得到满足,需要对上述增量迭代过程施加必要的约 峰值检测过程来求解问题5,即 束,迭代步长因子选择就是其中一种有效的手段.特 东=agm要r(r)=∑m(5)w,(5-). 别地,通过选择合适的迭代步长因子,将式(13)、 其等价地可以写成: (14)中的加性迭代模式转化为乘性迭代模式,就能 够满足非负约束的要求.为此,分别选取6u和?:为 arg mr(w.O.). []a c 注解8T:(r)可以看成M和W⊙,的一种相似 e=[r门g:=tr(wwo) 性度量,即上述激活时间的估计过程是一种基于相 则试(13)、(14)可以重新表示成以下乘性迭代模式: 似性最大化准则的策略。 [MA] []u←[]ai门 (15) 3实验结果 tr(Mwe.) 笔画是文字的最小构成单位,也是最小的文字 c←c tr(fwwe..) (16) 书写过程.文字手写过程中,除了笔画本身,相邻笔 求解上述问题4的算法总结如下:在初始化 画之间的连接模式也是手写技能的重要表现.通过 和c的基础上,每一轮的交替迭代可以首先利用上 切分文字手写运动轨迹,获得笔画及其连接模式在 一轮c的估计值计算出,进而利用式(16)更新c, 手写运动分析和理解中有着重要的作用.例如,笔画 在此基础上用式(15)更新,对比上一轮和本轮 及其连接的光滑性可以用于辅助运动神经控制疾病 J(0,c)的值,若无明显变化,就结束迭代过程,否则 的诊疗[801.然而,在手写识别中广泛采用的基于 继续重复交替迭代过程. 时间或空间点的切分策略52],无法揭示相邻笔画 2.2激活时间参数的估计 重叠的连接模式,本文基于生物运动神经控制机理, 由式(1)或(3)知道,w:(t-T:)对生成m(t)的 将协作基元作为手写运动的最小构成单位,形成能 贡献仅限于区间supp(w:(t-T:).换言之,w:(t- 够揭示相邻笔画重叠连接模式的合成分析方法,较 T:)与m(t)在supp(w:(t-T:))上的波形最有可能 已有的非重叠切分策略对比,基于协作基元合成分 匹配.因此,若将c:W⊙,作为波形模板,通过与M 析的笔画切分方法具有更为广泛的适用性.本节将 进行匹配,就有可能确定出supp(w:(t-T:))或者激 以手写字母‘p'的笔画切分为例,验证手写运动协 活时间T·基于上述思想,将问题3的求解问题归结 作基元提取方法的有效性,实验流程如图2所示. 为以下优化问题 问题5对于每个i,c:≠0,确定激活时间:使得 i:=arg minV:(r)=:‖M-c,W⑨,‖, 式中:Y定义为 化 Y;=t;I supp(w;(t-t;))C supp(m(t)). 循环:交替迭代 (17) 输出Fc 结计成 注解7式(17)给出了保证模板整体匹配的允 结参数 构r 新,更新 许参数r的集合.特别地,对Hr∈Y:,有 始化和c ∑w,-)2=Iw).(18) 容易验证V:()可以等价地表示为 图2字母‘p'的笔画切分实验流程 ()=[m(g)-cm,(g-1 Fig.2 Diagram of stroke segmentation for letter'p' 图2前2个环节描述了字母‘p'的一次连续手 d:-2cr(T). 写运动数据采集过程.采用WACOM公司的数位板 式中: Graphire4CTE440作为手写输人设备,最大读取速 d=:∑【m()2+clw,()I2], 度为100点/s,采样误差小于±0.5mm.通过数位 r(r)=∑m()w,(5- .(19) 板获取笔端的运动轨迹序列,将其转换成X轴和Y 特别地,式(19)与参数?的无关特性是由等式关系 轴速率序列.为了去除书写过程的不确定性影响和
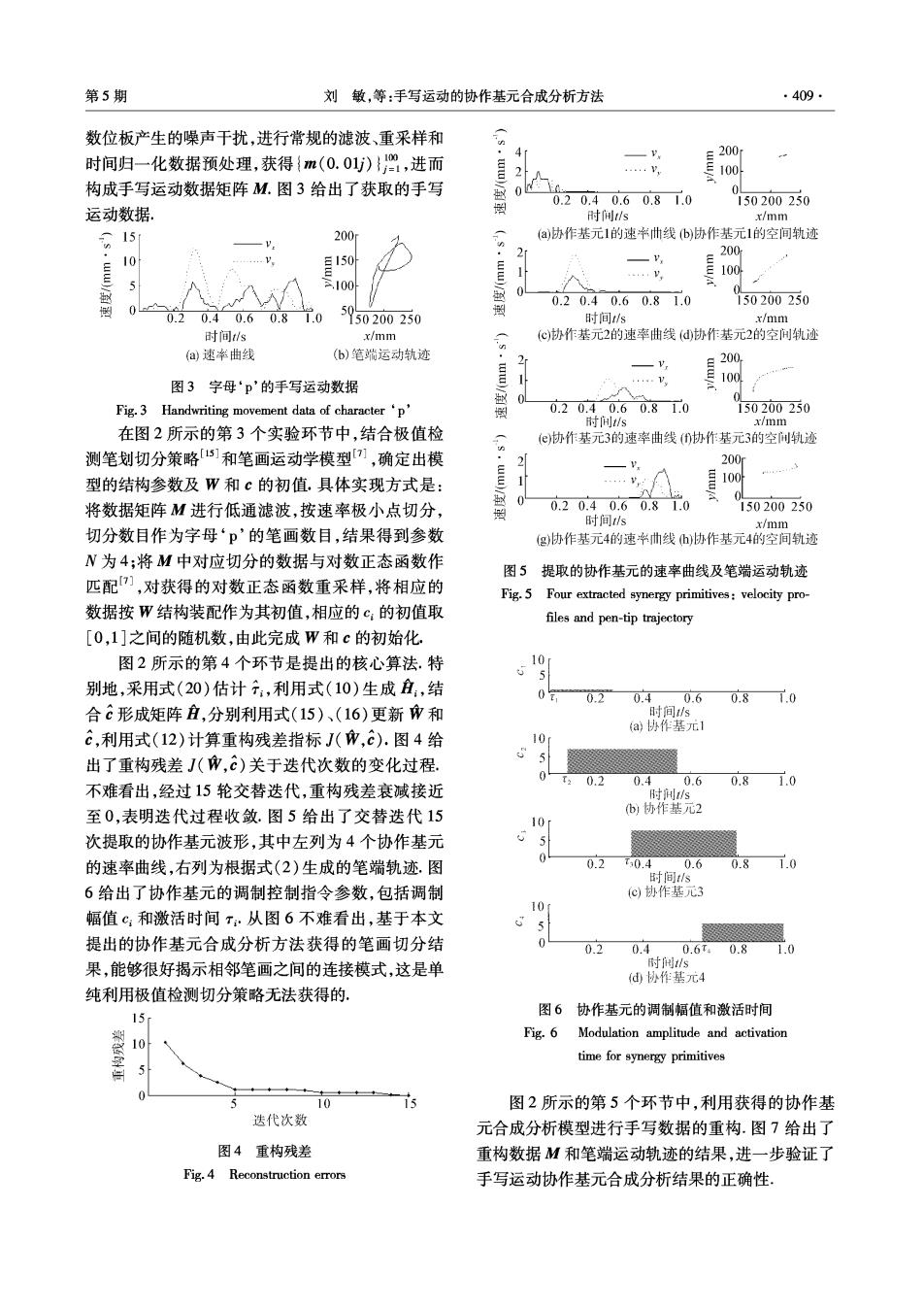
第5期 刘敏,等:手写运动的协作基元合成分析方法 ·409· 数位板产生的噪声干扰,进行常规的滤波、重采样和 时间归一化数据预处理,获得{m(0.01j),进而 4 200, 2 …vy 构成手写运动数据矩阵M.图3给出了获取的手写 具100 裂 0.20.40.60.81.0 150200250 运动数据。 时间t/s x/mm 15 200 (a)协作基元1的速卡州线(b)协作基元1的空间轨迹 E150 2 200 10 V ≥100 0 0.20.40.60.81.0 150200250 0 0.20.40.60.81.0 150200250 删 时间t/s x/mm 时间tls x/mm (c)协作基元2的速率曲线(协作基元2的空问轨迹 a)速率曲线 ()笔端运动轨迹 图3字母‘p'的手写运动数据 1 … 目微 0 Fig.3 Handwriting movement data of character'p' 綱 0.20.40.60.81.0 50200250 时间/s x/mm 在图2所示的第3个实验环节中,结合极值检 (e)协作基元3的速率曲线(0协作基元3的空问轨迹 测笔划切分策略15]和笔画运动学模型),确定出模 200 型的结构参数及W和c的初值.具体实现方式是: 写100 0 将数据矩阵M进行低通滤波,按速率极小点切分, 爱 0.20.40.60.81.0 150200250 时间t/s x/mm 切分数目作为字母‘p’的笔画数目,结果得到参数 (g)协作基元4的速兴曲线山)协作基元4的空间轨迹 N为4;将M中对应切分的数据与对数正态函数作 图5 提取的协作基元的速率曲线及笔端运动轨迹 匹配),对获得的对数正态函数重采样,将相应的 Fig.5 Four extracted synergy primitives:velocity pro- 数据按W结构装配作为其初值,相应的℃:的初值取 files and pen-tip trajectory [0,1]之间的随机数,由此完成W和c的初始化. 图2所示的第4个环节是提出的核心算法.特 10 别地,采用式(20)估计分,利用式(10)生成a,结 09 0.2 0.4 0.60.8T.0 合c形成矩阵,分别利用式(15)、(16)更新0和 时间/s a)协作基元1 c,利用式(12)计算重构残差指标J(,c).图4给 10 出了重构残差J(0,c)关于迭代次数的变化过程. T20.2 0.4 0.6 0.8 1.0 不难看出,经过15轮交替迭代,重构残差衰减接近 时间s 至0,表明迭代过程收敛.图5给出了交替迭代15 b)协作基元2 10 次提取的协作基元波形,其中左列为4个协作基元 0 的速率曲线,右列为根据式(2)生成的笔端轨迹.图 0.2 T30.4 0.6 0.8 1.0 时间/s 6给出了协作基元的调制控制指令参数,包括调制 (C)协作基元3 10 幅值℃:和激活时间T·从图6不难看出,基于本文 5 提出的协作基元合成分析方法获得的笔画切分结 0 0.2 0.4 0.6T40.8 1.0 果,能够很好揭示相邻笔画之间的连接模式,这是单 时间ls d协作基元4 纯利用极值检测切分策略无法获得的, 图6协作基元的调制幅值和激活时间 15 Fig.6 Modulation amplitude and activation 10 time for synergy primitives 10 图2所示的第5个环节中,利用获得的协作基 迭代次数 元合成分析模型进行手写数据的重构.图7给出了 图4重构残差 重构数据M和笔端运动轨迹的结果,进一步验证了 Fig.4 Reconstruction errors 手写运动协作基元合成分析结果的正确性

410 智能系统学报 第5卷 15 一,x重构的v 200 [10]LATASH M L,SCHOLZ J P,SCHONER G.Toward a 10 ·”,*重构的v E150 new theory of motor synergies[J].Motor Control,2007, 11(3):276-308. .100 [11]GHAHRAMANI Z.Building blocks of movement[J].Na- 02 50 0.2 0.40.60.81.0 50200250 tue,2000,407(12):682-683. 时间/s x/mm [12]HOFER J,GRUBER C,SICK B.Biometric analysis of ()协作基元重构的速系t线(b)协作基元重构的轨迹 handwriting dynamics using a script generator model[C]/ 图7重构结果 Proceedings of IEEE Mountain Workshop on Adaptive and Fig.7 Reconstruction results Learning Systems.Logan,USA,2006:36-41. [13]FLASH T,HANDZEL A.Affine differential geometry a- 4结束语 nalysis of human arm movements[J].Biological Cybernet- ic8,2007,96(6):577601. 本文将运动神经控制认知中协作基元的概念引 [14]MUSSA-IVALDI F A,BIZZI E.Motor learning through the 入到手写运动分析过程,研究手写运动数据协作基 combination of primitives[J].Philosophical Transactions: 元合成分析方法,提出了交替迭代的实现策略,是对 Biological Sciences,2000,355(1404):1755-1769. 手写运动数据分析方法的丰富和发展, [15 ]HOLTSBERG A,STERNBY J.Segmentation-based recog- nition:United States,US 2006/0110041 A1[P].2005- 运动协作基元可以看成运动发生过程中具有独 1109. 立生物运动神经控制意义的最小构成单位,手写运 [16]NOVAK K E,MILLER L E,HOUK J C.The use of over- 动协作基元合成分析方法更有助于精细地解析观测 lapping submovements in the control of rapid hand move- 数据背后手写运动发生的模式,这一方式具有相当 ments[J].Experimental Brain Research,2002,144: 的普适性,更符合生物运动神经控制规律.针对手写 351-364. [17]GLASER E M,RUCHKIN D S.Principles of neuronbio- 笔画切分的实验研究结果表明,协作基元合成分析 logical signal analysis[M].New York:Academic Press, 结果能有效揭示相邻笔画可能的重叠连接模式,可 1976:239-245. 进一步应用于模式识别、仿人机器人、辅助运动神经 [18]ROHRER B,FASOLI S,KREBS H I,et al.Movement 损伤康复诊断以及人机交互等领域 smoothness changes during stroke recovery[J].Joural of Neuroscience,2002,22(18):8297-8304. 参考文献: [19]VINJAMURI R.CRAMMOND D J.KONDZIOLKA D.et al.Extraction of sources of tremor in hand movements of [1]WOLPERT D M,GHAHRAMANI Z.Computational princi- ples of movement neuroscience[J].Nature Neuroscience, patients with movement disorders[J].IEEE Transactions on Information Technology in Biomedicine,2009,13(1): 2000,3:1212-1217. 49-56. [2]WINTER D A.Biomechanics and motor control of human [20]DIPIETRO L,KREBS H I,FASOLI S E,et al.Changing movement[M].2nd ed.New York:John Wiley and Sons, 2004:1444. motor synergies in chronic stroke[J].J.Neurophysiology, 2007,98(2):757-768. [3]JENKINS O C,MATARIC M J.Deriving action and behav- ior primitives from human motion data[C]//Proceedings of [21]LEE J,YOON H S,SOH J,et al.Using geometric extre- IEEE/RSJ International Conference on Intelligent Robots ma for segment-to-segment characteristics comparison in and Systems.Lausanne,Switzerland,2002:2551-2556 online signature verification[J.Pattern Recognition, [4]BIZZI E.Motor primitives and rehabilitation[C]//Proceed- 2004,37:93-103 作者简介: ings of Virtual Rehabilitation.Venice,Italy,2007:20-22. 刘敏,女,1976年生,博士研究 [5]SCHOMAKER L.From handwriting analysis to pen-comput- er applications[J].Electronics Communication Engineer- 生,主要研究方向为生物信息处理 ing Journal,1998,10(3):93-102. 6]MARQUARDT C,MAI N.A computational procedure for movement analysis in handwriting[J].Joural of Neuro- science Methods,1994,52(1):39-45 7]PLAMONDON R,DJIOUA M.A multi-level representation paradigm for handwriting stroke generation [J].Human Movement Science,2006,25(4/5):586-607. 王国利,男,1965年生,教授、博士 8]POLYAKOV F,DRORI R,BEN-SHAUL Y,et al.A com- 生导师,德国洪堡学者,中国人工智能 pact representation of drawing movements with sequences of 学会智能空天系统专业委员会委员,主 parabolic primitives[J].PLoS Computational Biology, 要研究方向为信息获取与信息处理 2009,5(7):1-18. 主持完成省部级科研项目6项,获得省 [9]BYE R T.The BUMP model of response planning[D]. 部级科技进步奖2次. Sydney,Australia:The University of New South Wales, 2009