
第5卷第4期 智能系统学报 Vol.5 No.4 2010年8月 CAAI Transactions on Intelligent Systems Aug.2010 doi:10.3969/j.issn.16734785.2010.04.013 ANFIS的板形控制动态影响矩阵方法 张秀玲,逢宗鹏,李少清,张少宇 (1.燕山大学电气工程学院,河北秦皇岛066004:2.燕山大学工业计算机控制工程河北省重点实验室,河北秦皇岛066004) 摘要:针对板形控制系统的非线性和强耦合性,以及传统效应函数法和板形静态影响矩阵法的不足,通过对大量 生产实测数据的计算和分析,提出了板形控制的动态影响矩阵法.通过基于减法聚类的ANFS(自适应神经模糊推 理系统)的板形动态矩阵预测模型,在线求得不断变化的影响矩阵,兼顾了板带生产的实时性与复杂性,仿真实验验 证了其有效性。 关键词:板形控制;自适应神经模糊推理系统:影响炬阵;聚类;模糊 中图分类号:TP18文献标识码:A文章编号:16734785(2010)040360-06 A dynamic influence matrix method for flatness control based on adaptive-network-based fuzzy inference systems ZHANG Xiu-ling,PANG Zong-peng,LI Shao-qing,Zhang Shao-yu (1.College of Electrical Engineering,Yanshan University,Qinhuangdao 066004,China;2.Key Lab of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao 066004,China) Abstract:Flatness control systems have both strong nonlinearity and coupling.Unfortunately traditional effective function methods and the static influrence matrix of flatness can not effectively solve such problems.After analysis of a large volume of production data a new method was proposed,a dynamical influence matrix method for the flat- ness controller.Using the predictive model of the dynamic flatness matrix,and incorporating the subtractive cluste- ring of an Adaptive Neuro-Fuzzy Inference System (ANFIS),the influence matrix was calculated in real time. Both the need for real-time results and the complexities of strip steel production were accommodated.Simulations confirmed the validity of the proposed method. Keywords:flatness control;adaptive neuro-fuzzy inference system;effective matrix;clustering;fuzzy8.there was use of flatness matrix'in Google scholar,but neither static'nor effective'were used before flatness matrix 板形控制技术是现代高精度板带轧制中的关键文提出了板形控制的动态影响矩阵方法,建立了基 技术之一.带钢的轧制过程涉及大量非线性因素,而 于ANIS网络的板形控制影响矩阵预测模型,根据 且轧制过程中的某些条件还具有时变和强耦合特 轧制过程中状态的不断变化,有效地进行板形调整 性,难以建立精确的数学模型,是板形控制中的难 量的改变,实现板形控制,以达到更高的精度, 点.目前,国内外许多有先进板形控制手段的轧机, 1板形控制的影响矩阵设计方法 其板形控制方案的制定,缺乏严密完整的理论基础 和精确快速的数学模型,往往通过大量生产实验摸 1.1影响矩阵的概述 索进行,不但造成财物的大量消耗,而且也制约了控 根据轧机的板形控制功能和工艺实况,选择勒让 制精度和成材率的提高15).因此,全面深人地研究 德正交多项式确定板形缺陷的6种基本模式分别是左 板形控制理论,建立新的精确快速的板形控制模型, 边浪、右边浪、中浪、双边浪、正四分浪和反四分浪1,6, 已经成为板形控制技术发展的必然和迫切要求.本 基于这6种板形基本模式,板形偏差可表示为 △o(y)=aP1(y)+a2P2(y)+a3P3(y), 收稿日期:200906-13. 式中:a1、a2、a3为板形特征值;P1(y)、P2(y)、P3(y) 基金项目:国家自然科学基金资助项目(50675186). 分别为勒让德一次、二次和四次多项式,如式(1)~ 通信作者:张秀玲.E-mail:ysu@yahoo.com.cm, (3)所示:

第4期 张秀玲,等:ANFIS的板形控制动态影响矩阵方法 .361· P1(y)=y, (1) 1.2板形控制的动态影响矩阵方法设计 )=子- (2) 1.2.1板形预测模型 板形控制系统是一个复杂的多变量、多扰动、强 ()=8(35y-30y2+3). (3) 耦合的非线性控制系统,若采用传统的数学方法建 模具有相当难度,而且精度也不能满足板形在线控 现阶段冷轧机生产中,常用的板形调节手段主 制的要求.因此,相比之下,采用智能方法来建立板 要有倾辊调节、弯辊调节、中间辊横移调节以及交叉 形模型具有一定的优越性78], 角和冷却等手段,定义影响系数为板形控制手段单 自适应神经模糊推理系统(ANFIS)是基于数据 位调节量引起的板形改变量,各种调节手段对板形 的一种建模方法,使用一些给定的输入输出数据集 的影响效果如式(4)~(6)所示四, 构建一个模糊推理系统,其隶属度函数参数可用反 f)=AA)=cp,o)+c,)+6,g. 向传播法与最小二乘法相结合的混合学习算法进行 △x1 调节,允许模糊系统用要建模的数据进行学习,使隶 (4) 属度函数适应输入输出数据.并且模糊规则是通过 E)=AAg)=cap,)+ca,)+6w,g), 对大量已知数据的学习得到的,而不是基于经验或 △x2 是直觉任意给定的.这对于那些特性还不被人们所 (5) ()=△(4a) 完全理解或者特性非常复杂的系统是尤为重要的 △x3 =c3P1(y)+cP2(y)+cP3(y): 所以,ANFIS既可表达模糊语言变量又具有学习功 能912.因此,ANFIS非常适合用来建立板形的预测 (6) 模型。 式中:f(y)(y)f3(y)分别为倾辊、弯辊和中间辊 虽然ANFIS的模糊规则具有很强的自学习能 横移影响函数;△(△o1)、△(△σ2)、△(△σ3)分别为 倾辊、弯辊和中间辊调节对残余应力的改变,△x1、 力,但是由于板形的影响因素众多,导致模型输入增 多,使其训练后会存在大量的模糊规则(其个数为 △x2、△x3分别为倾辊量、工作辊弯辊力和中间辊横 各概念逻辑划分数目的乘积),此时网络训练所花 移改变量,cg为影响系数.由△x1、△x2、△x3引起的板 形变化为 费的时间成倍增加,而网络的结构也越发庞大,引起 了“规则爆炸”现象,造成了学习效果的不明显,产 △(△o)=f(y)△x1+f(y)△x2+f(y)△3.(7) 将式(4)~(6)代入式(7)得: 生的大量冗余信息也极大的影响了控制的精度和计 算速度12].因此,本文根据影响系数矩阵的特性 △(△o)=△aP1(y)+△a2P2(y)+△a3P3(y). 分析及求解动态影响矩阵问题的特点,建立了一种 (8) 全新的基于减法聚类的ANFIS板形预测模型,大幅 式中: 度地提高了预报系统精度和鲁棒性, r△a1 cn C12 △x1 尽可能多地考虑了多种影响板形的因素,网络 △a2 C21 C22 C23 △x2 (9) 的输入层节点个数由影响板形的因素决定,确定为 △a -C31 C32 C33 △3 14个,其中11个为轧制基本参数,分别为来料板宽 令 B、入口平均厚度,、出口平均厚度五,、轧制压力 [cu C12 C13 △a1 P(bar)、前张力T、后张力T。、泊松比Y、工作辊直 C= C21 C22 C23 ,△A= △a2 △X △2 径D.、中间辊辊径Dm和支撑辊径D。、轧制温度 -C31 C32 C33 ,△a3 △x3 T(℃):3个为调节参数,分别为倾辊调节量x1、工 (10) 作辊弯辊力2、中间辊横移量3·网络输出为3个 则有 反应板形模式与大小的特征值,即板形特征值a1、a2 △A=C△X, (11) 和a3·板形预测模型拓扑结构如图1所示. 式中:C定义为影响系数矩阵或影响矩阵C,矩阵元 1.2.2影响矩阵预测漠型的设计 素C:为影响系数,其物理意义为第j种板形调节量 影响板形的因素众多,而且关系复杂,板形各调 单位变化对第i种板形模式的影响系数;△A为板形 节手段对板形的影响和调节效果难以用机理模型准 特征参数的变化量;△X为板形调解手段的改变 确描述,另外,机理模型复杂的运算难以满足板形在 量2, 线控制实时性的要求,为此,本文提出从轧制时测得
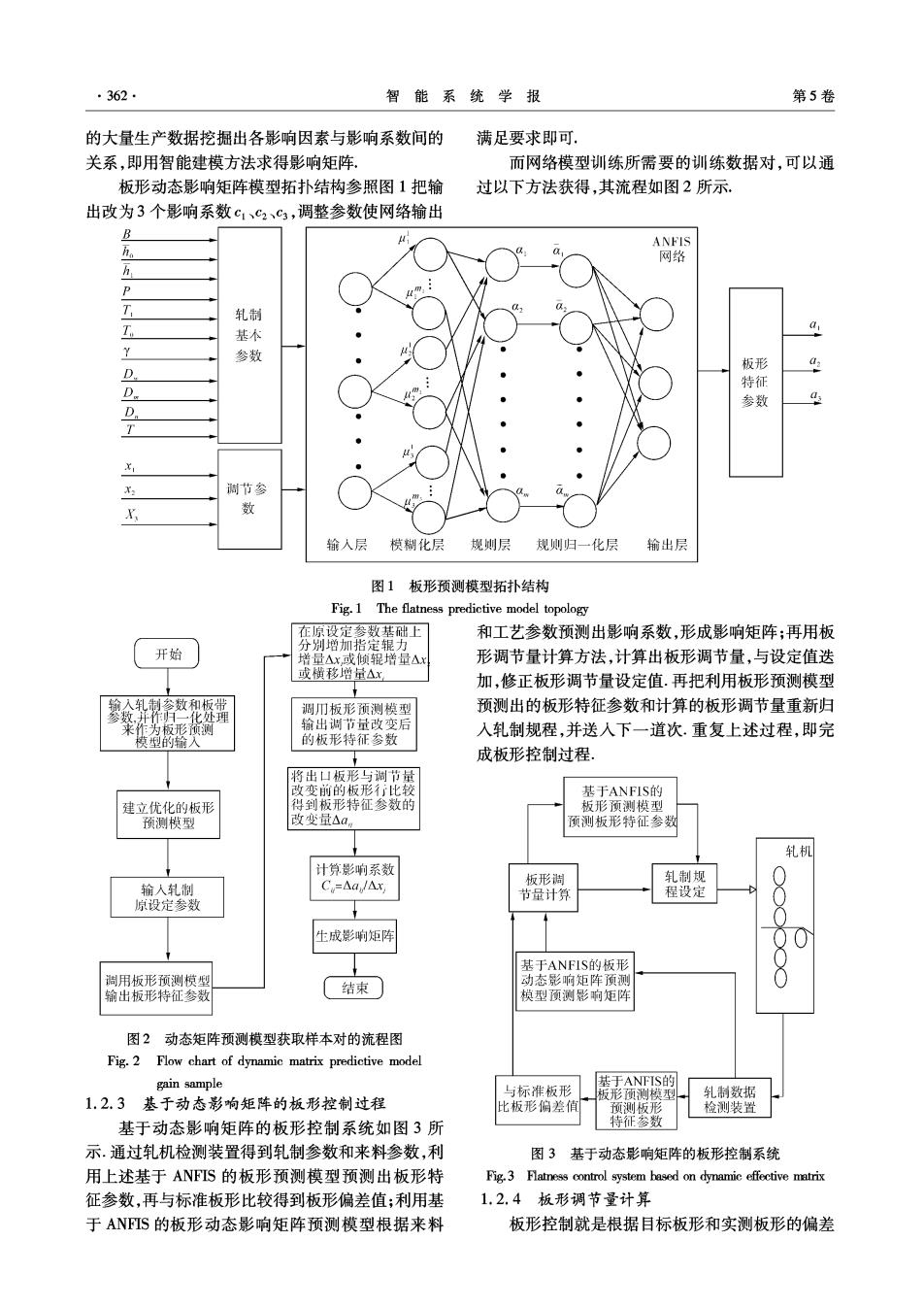
362. 智能系统学报 第5卷 的大量生产数据挖掘出各影响因素与影响系数间的 满足要求即可. 关系,即用智能建模方法求得影响矩阵。 而网络模型训练所需要的训练数据对,可以通 板形动态影响矩阵模型拓扑结构参照图1把输 过以下方法获得,其流程如图2所示. 出改为3个影响系数c1、c2、C3,调整参数使网络输出 B ANFIS 网络 P T 轧制 T. 基不 0 Y 参数 板形 D 特征 D 参数 D T X X2 调节参 X 数 输入层模制化层 规则层规则归一化层 输出层 图1板形预测模型拓扑结构 Fig.1 The flatness predictive model topology 在原设定参数基础上 和工艺参数预测出影响系数,形成影响矩阵;再用板 分别增加指定辊力 开始 增量△x或倾辊增量△x 形调节量计算方法,计算出板形调节量,与设定值迭 或横移增量△x 加,修正板形调节量设定值.再把利用板形预测模型 预测出的板形特征参数和计算的板形调节量重新归 处理 调巾板形预测模型 来作为板形预测 输出调节量改变后 模型的输入 的板形特征参数 入轧制规程,并送人下一道次.重复上述过程,即完 成板形控制过程, 将出口板形与调节量 改变前的板形彳比较 基于ANFIS的 建立优化的板形 得到板形特征参数的 板形预测模型 预测模型 改变量△a 预测板形特征参数 轧机 计算影响系数 轧制规 输人轧制 C=Aa/Ax 板形调 节量计算 程设定 原设定参数 生成影响炬阵 基于ANFIS的板形 调用板形预测模型 动态影响矩阵预测 输出板形特征参数 结束 摸型预测影响炬阵 图2动态矩阵预测模型获取样本对的流程图 Fig.2 Flow chart of dynamic matrix predictive model gain sample 基于ANFIS的 与标准板形 轧制数据 1.2.3基于动态影响矩阵的板形控制过程 板形预测模型 比板形偏差值 预测板形 检测装置 基于动态影响矩阵的板形控制系统如图3所 特征参数 示.通过轧机检测装置得到轧制参数和来料参数,利 图3基于动态影响矩阵的板形控制系统 用上述基于ANFIS的板形预测模型预测出板形特 Fig.3 Flatness control system based on dynamic effective matrix 征参数,再与标准板形比较得到板形偏差值;利用基 1.2.4 板形调节量计算 于ANFIS的板形动态影响矩阵预测模型根据来料 板形控制就是根据目标板形和实测板形的偏差

第4期 张秀玲,等:ANFIS的板形控制动态影响矩阵方法 ·363· 来确定各个控制手段的调节量.板形调节量计算主 板形调节量应为-△X, 要包括倾辊调节量、工作辊弯辊调节量和中间辊横 移量的计算,板形调节量计算的核心思想是板形偏 2 动态影响矩阵法在900HC轧机上 差的最小化,本文利用的计算方法为影响矩阵法.即 的仿真应用 如式(12)所示. △X=C-△A. (12) 以900mmHC六辊轧机为对象,某一带材:轧制 根据检测出的板形特征参数的改变量:△A= 规格:2.2×4820.248×482材质:SPHC.就该带材 △a1 为例,就某板形缺陷分别进行了工作辊弯辊控制方 △a2 ,利用已经建立的动态影响矩阵预测模型可 法调整,中间辊横移控制方法调整,以及2种方法共 .△3 同控制调整,仿真结果分别如表2~表4所示.由于 以预测影响矩阵C,即可迅速算出板形调节量: 在轧机的奇数道次安装了板形仪,1、3、5道次板形 △x1 结果如图4~6所示。 △X= △x2 1)工作辊弯辊控制仿真结果 L△x3 板形控制的目的是消除板形偏差,所以实际的 表1工作辊弯辊控制方法仿真结果 Table 1 The simulation result of work roll bending control method 工作辊弯辊 第1道次 第2道次 第3道次 第4道次 第5道次 C=-0.83 c1=-0.83 c1=-0.55 c1=-177.45 c1=-177.45 影响矩阵参数 c2=88.31 c2=87.92 c2=0.33 c2=-0.82 c2=6.27 c3=-79.20 c3=-78.86 c3=1.08 c3=0.70 c3=3.77 a1=0.5447 a1=0.5636 a1=0.5104 a1=0.4011 a1=0.3968 板形特征参数 a2=-0.8129 42=-0.3081 a2=-0.2321 a2=0.1313 42=0.1300 a3=0.1644 a3=-0.2958 a3=-0.3536 a3=-0.1239 a4=-0.1225 5 0 0050005 时间s 00.500.5 归…化板宽 200500050 时间s 0500.5 妇一化板宽 09500500-1-05D057 时间ts 归一化板宽 a筑1道板形输出显示 b筛2道板形输出显示 (C第3道板形输出显示 图4(a)~(c)工作辊弯辊控制板形结果 Fig.4 (a)~(c)The flatness result of work roll bending control 2)中间辊横移控制仿真结果 205000500-10300.51 时间ts 妇一化板宽 500050 时间s 10.50051 织一化板宽 2050100500--0.5005 时间s 归…化板宽 (a第1道板形输出显示 b)第3道板形输出显示 (c第5道板形输出显示 图5(a)~(c)中间辊横移控制板形结果 Fig.5 (a)~(c)The flatness result of middle roll shiftting control
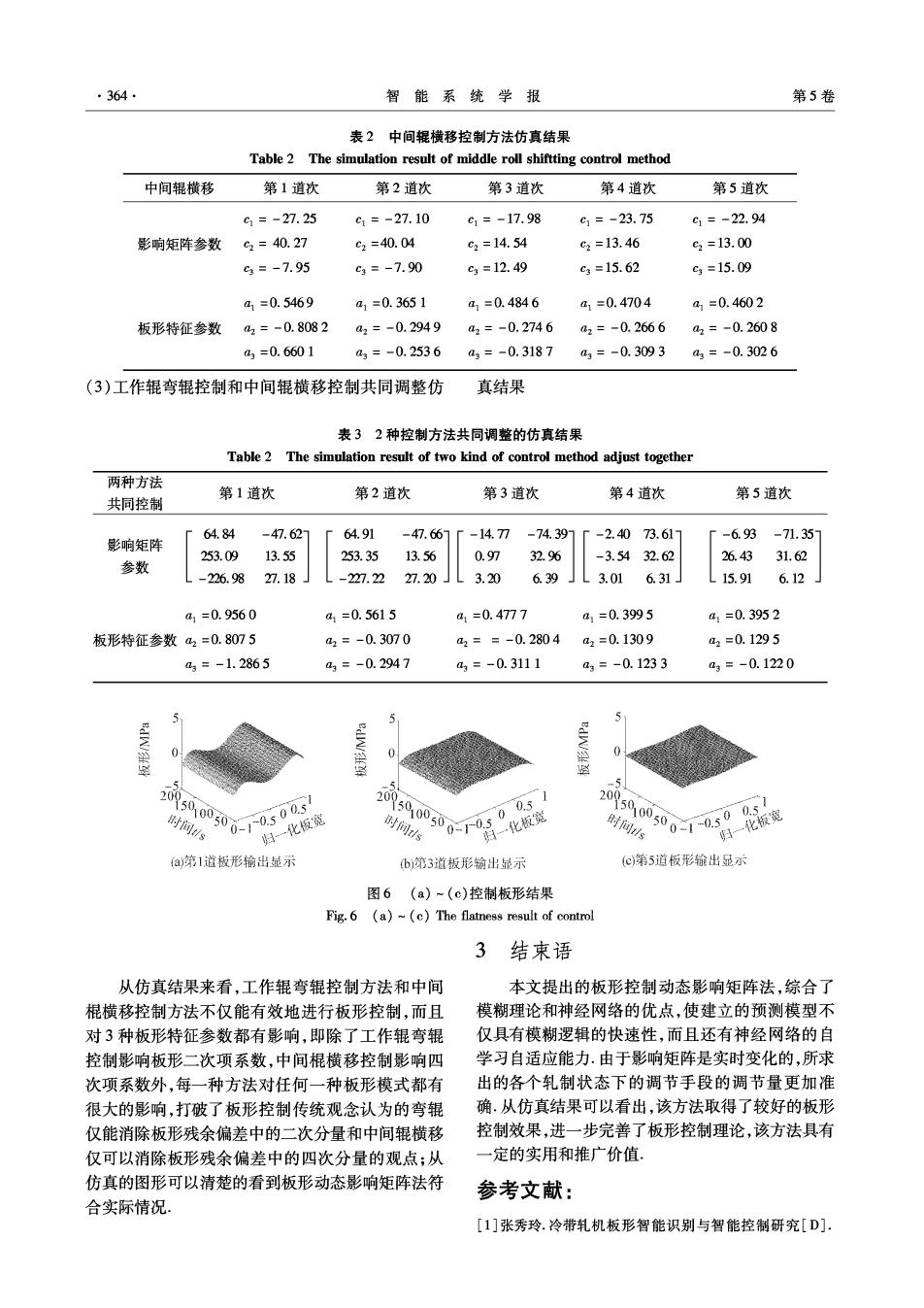
364 智能系统学报 第5卷 表2中间辊横移控制方法仿真结果 Table 2 The simulation result of middle roll shiftting control method 中间辊横移 第1道次 第2道次 第3道次 第4道次 第5道次 c1=-27.25 c1=-27.10 c1=-17.98 c1=-23.75 G1=-22.94 影响矩阵参数 c2=40.27 c2=40.04 c2=14.54 c2=13.46 92=13.00 c3=-7.95 c3=-7.90 c3=12.49 c3=15.62 c3=15.09 a1=0.5469 a1=0.3651 a1=0.4846 a1=0.4704 a1=0.4602 板形特征参数a2=-0.8082 a2=-0.2949 a2=-0.2746 a2=-0.2666 a2=-0.2608 a3=0.6601 a3=-0.2536 a3=-0.3187 a3=-0.3093 a3=-0.3026 (3)工作辊弯辊控制和中间辊横移控制共同调整仿 真结果 表32种控制方法共同调整的仿真结果 Table 2 The simulation result of two kind of control method adjust together 两种方法 共同控制 第1道次 第2道次 第3道次 第4道次 第5道次 64.84 -47.62 64.91 -47.66 -14.7T7 -74.39 -2.4073.61 -6.93 -71.35 影响矩阵 253.09 13.55 253.35 13.56 0.97 32.96 -3.5432.62 26.43 31.62 参数 -226.98 27.18 -227.22 27.20 3.20 6.39 3.01 6.31」 L15.91 6.12 a1=0.9560 a1=0.5615 a1=0.4777 a1=0.3995 a1=0.3952 板形特征参数42=0.8075 a2=-0.3070 a2==-0.2804 a2=0.1309 a2=0.1295 a3=-1.2865 a3=-0.2947 a3=-0.3111 a3=-0.1233 a3=-0.1220 W/ 10500050 时间s 105005 归一化板宽 30o0300 时间s 00. 归…化板宽 2015000500-1-0.50031 时间s …化板宽 a)第1道板形输出显示 b)第3道板形输出显示 (©)第5道板形输出显示 图6(a)~(c)控制板形结果 Fig.6 (a)~(c)The flatness result of control 3结束语 从仿真结果来看,工作辊弯辊控制方法和中间 本文提出的板形控制动态影响矩阵法,综合了 棍横移控制方法不仅能有效地进行板形控制,而且 模糊理论和神经网络的优点,使建立的预测模型不 对3种板形特征参数都有影响,即除了工作辊弯辊 仅具有模糊逻辑的快速性,而且还有神经网络的自 控制影响板形二次项系数,中间棍横移控制影响四 学习自适应能力.由于影响矩阵是实时变化的,所求 次项系数外,每一种方法对任何一种板形模式都有 出的各个轧制状态下的调节手段的调节量更加准 很大的影响,打破了板形控制传统观念认为的弯辊 确.从仿真结果可以看出,该方法取得了较好的板形 仅能消除板形残余偏差中的二次分量和中间辊横移 控制效果,进一步完善了板形控制理论,该方法具有 仅可以消除板形残余偏差中的四次分量的观点;从 一定的实用和推广价值。 仿真的图形可以清楚的看到板形动态影响矩阵法符 参考文献: 合实际情况 [1]张秀玲.冷带轧机板形智能识别与智能控制研究[D]

第4期 张秀玲,等:ANFIS的板形控制动态影响矩阵方法 ·365· 秦皇岛:燕山大学,2002. [9]吴晓莉,林哲辉.MATLAB辅助模糊系统设计[M].西 ZHANG Xiuling.Research on intelligent control and recog- 安:西安电子科技大学出版社,2002:6293 nition of flatness for cold strip mill[D].Qinhuangdao:Yan- Wu Xiaoli,Lin Zhehui.MATLAB Aided Fuzzy System De- shan University,2002. sign[M].Xi'an:Xi'an University of Electronic Science [2]何海涛.宽带钢冷轧机板形在线控制智能模型的研究与 and Technology Press,2002:62-93 应用[D].秦皇岛:燕山大学,2008。 [10]YING LC,PAN M C.Using adaptive network based fuzzy HE Haitao.Research on flatness on-line intelligent control inference system to forecast regional electricity loads[J]. for the wide strip steel cold mill[D].Qinhuangdao:Yans- Energy Conversion and Management,2008,49:205-211 han University,2008. [11]张阿卜.基于减法聚类和自适应神经模糊推理系统的 [3]刘建昌,陈莹莹,张瑞友.基于PS0.BP网络的板形智能 递阶模糊系统的设计[J].控制理论与应用,2004,21 控制器[J].控制理论与应用,2007,24(4):674678. (3):415418. LIU Jianchang,CHEN Yingying,ZHANG Ruiyou.Intelli- ZHANG Abu.Design of hierarchical fuzzy system via sub- gent flatness-controller based on PSO-BP network[J].Jour- tractive clustering and ANFIS[J].Joural of Control Theo- nal of Control Theory and Application,2007,24(4):674- ry and Application,2004,21(3):415-418. 678. [12]杨新,张陶红,余刚,柴天佑.基于ANIS的选矿产品成 [4]RINGWOOD J V.Shape control systems for sendzimir steel 本预测模型[J].系统仿真学报,2007,19(24):5688- mills[J].IEEE Transactions on Control Systems Technolo- 5691. 罗,2000,8(1):7086. YANG Xin,ZHANG Taohong,YU Gang,CHAI Tianyou. [5]ZARATE L E,BITTENCOUT F R.Neural networks and Mineral processing product cost forecasting model based on fuzzy rules based control for cold rolling process via sensitiv- ANFIS[J].Joumal of System Simulation,2007,19(24): ity factors[C]//27th Annual Conference of the IEEE Indus- 56885691 trial Electronics Society.Piscataway,NJ,USA,2001:64- 作者简介: 69. 张秀玲,女,1968年生,博士,教授, [6]LIU Hongmin,ZHANG Xiuling,WANG Yingrui.Transfer 从事神经网络智能控制研究,获国家科 matrix method of flatness control for strip mills[J].Joural 技进步二等奖一项,省部级科技进步一 of Materials Processing Technology,2005,166(2):237- 等奖、二等奖各一项,发表论文60余 242. 篇。 [7]贾春玉,单修迎,牛召平.自调整动态神经网络模型及其 在带材板形预测中的应用[J].钢铁研究学报,2006,18 (12):50-53. 逢宗朋,男,1983年生,硕士研究 JIA Chunyu,SHAN Xiuying,NIU Zhaoping.Self-adjusting 生,研究方向为模糊神经网络优化板形 dynamic neural network model and its application in strip 设计. shape prediction[J.Joural of Iron and Steel Research. 2006,18(12):5053. [8]贾春玉,单修迎,刘宏民,邱格君.模糊神经板形控制模 型在冷轧带钢生产中的应用[J].冶金设备,2008,1:1-5 JIA Chunyu,SHAN Xiuying,LIU Hongmin,QIU Gejun. Application of fuzzy nerve flatness control model in cold roll- ing[J].Metallurgical Equipment,2008,1:1-5