
第5卷第2期 智能系统学报 Vol.5 No.2 2010年4月 CAAI Transactions on Intelligent Systems Apr.2010 doi:10.3969/j.issn.16734785.2010.02.010 6R关节型机器人运动学建模 王立权,刘秉昊2,吴健荣,韩金华1,卢正宇1 (1.哈尔滨工程大学机电工程学院,黑龙江哈尔滨150001;2.哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:为满足新开发的多机器人实验系统编程需要,研究了6R机器人运动学逆解问题推导了代数逆解结果,并 研究了将其用于实际控制系统时,逆解的漏解、增根和多解问题.与传统方法比较,采用了便于程序模块化的坐标系 设置方式,在需要经常更换作业工具的多机器人系统中更为适用.推导过程只需2次矩阵逆乘,步骤简单.基于VC+ +和OpenGL技术编制了系统程序,检验了方法的有效性.以其中一个位姿为例,对比几何方法得出的结果,验证了 算法的正确性.研究的结果适用于MOTOMAN-UP6和PUMA560等相似构型的所有机器人 关键词:逆运动学:机器人;代数解法 中图分类号:TP241文献标识码:A文章编号:16734785(2010)02-015605 Modeling and implementing the inverse kinematics of a six revolute joint robot WANG Li-quan',LIU Bing-hao2,WU Jian-rong,Han jin-hua',LU Zheng-yu (1.College of Mechanical and Electrical Engineering,Harbin Engineering University,Harbin 150001,China) Abstract:To program a new multi-robot system,inverse kinematic equations for a six revolute joint(6R)robot were developed.Their algebraic solutions were then derived.Conditions causing there to be no solution,extraneous roots,or multiple solutions for inverse kinematic equations were studied for equations used in the practical control of a system.Compared with traditional methods,this method is more suitable for a multi-robot system in which work- ing tools are frequently replaced.As only two inverse matrices were involved,the method was simple and easy.In order to verify the effectiveness of the method,it was compiled using VC++and OpenGL software.After selecting a specific position as an example,we proved the correctness of the algorithm by comparing its results to those from geometric analysis.The research is applicable to other robot systems with similar mechanical configurations,such as MOTOMAN-UP6 or PUMA560. Keywords:inverse kinematics:robot:algebraic solution 运动学逆解是机器人控制的基础,已有大量文 用的方便性,个别文献的理论推导还存在瑕疵, 献研究.机器人运动学逆解方法有很多,包括代数 文献[1]理论推导了PUMA560的运动学逆解 法、几何法、数值法,以及神经网络、遗传算法等智能 方程,文献[2-3]给出了一种求解MOTOMAN-UPJ 方法.其中,代数法结果精确、实时性好,在MOTO- 型机器人的逆解方法.文献[4]在文献[2]的基础上 MAN、PUMA型机器人控制中最为实用. 讨论MOTOMAN-SV3X型机器人逆解问题,注意到 为建立开放的多机器人协调作业实验平台,编 了机器人安装位置和所配工具的变化.由于使用反 制适用于多机器人、多工具系统的机器人逆解程序, 正弦、反余弦、反正切表示角度,文献[2]和文献[4] 笔者查阅了大量文献.发现绝大部分文献都是单个 都存在个别漏解问题,国内一些介绍机器人技术的 机器人逆解方法的理论研究,既不考虑实际控制中 专著中也有类似现象.此外,以上文献对推导的多组 非常重要的漏解、增根、多解问题,也不考虑编程应 解没有作进一步处理,其结果尚不能直接用于机器 人控制编程 收稿日期:2008-1220. 基金项目:黑龙江省自然科学基金重点资助项目(ZD200911) 本文结合课题需要,在文献[34]的基础上对逆 通信作者:王立权.E-mail:wangliquan@hrbeu.cdu.cm. 解方法进行改进,寻求一种准确可靠、实时性好、可

第2期 王立权,等:6R关节型机器人运动学建模 ·157· 移植、方便多机器人系统配置和工具换接的逆解方 工具点位姿,即解方程组T=T(01,02,…,06).先 法.基于VC++和OpenGL成功地开发了软件系 以T=T2T3T3T4TT得到正解算法的核心部分 统,将运动学算法融入到带实时三维仿真的控制系 8T=gT(01,02,…,06),再由"T=8T8TT得到最终 统,在实验系统上验证了解算结果, 结果 1D-H坐标系与运动学正解 2运动学逆解方程推导 本文研究的6R机器人结构如图1所示,按D-H 运动学逆解是已知末端位姿求解各关节角度, 法建立机器人坐标系,相应D-H参数如表1,连杆 即由T(0,02,…,06)=T确定的12个非线性方 变换矩阵如式(1).不同于其他文献,这里坐标系 程(其中仅有6个独立方程)来求解01,02,…,0。.由 {6}原点在机器人手腕点,用T表示工具坐标系{t} T=8T6T(01,02,…,06)T作变换可得 相对于坐标系{6}的位姿,增加T表示机器人基座 T(01,02,…,06)=(8T)-1rT(T)-,(2) 坐标系{0}相对于世界坐标系{or}的位姿.在多机 当给定。T和T,右边为常矩阵.于是,求逆解的 器人相对位置和联接工具经常变化的情况下,可根 核心问题是:已知gT,求01,02,…,06 据安装位置和工具形状修改每个机器人的。T和T 由8T=TT TTTST作变换,得: 矩阵,而无需修改核心的运动学算法,有利于软件系 3TT4T=(2T)1(T)-18T(T).(3) 左边: 1 式中: 3D.=a3c3-d43+42, 3p,=a33+d493, 图1连杆坐标系设置 3知.-0. Fig.1 Link-frame assignments 右边: 统的模块化. (2T)-(9T)48T(8T)-1= T= R'Lp:P.]"] Ci -s: o di-1 0 1 sicQi-1 cicai-1 -sQi-1 disqi-1 式中: (1) S:sC:-1C0:-1 cQ:-1 d;cqi- pi=cCaPs +sCaPy -saP:-ac2, 0 0 0 1 P =-c1SaPs-s1S2Py -c2P:a1s2, 式中:C:=cos0:,=sin0,ce:=c08c,sa:=sinc, p:=-siPs ciPy 以下类似. 1)求解01、02、03 表1连杆参数表 考虑式(3)左、右对应元素(3,4)相等,得01三 Table 1 Link parameters atan2(p,P)或0,=atan2(-Py,-p.) a-1/()a-1/mmd,/mm/()变量范围/() 考虑式(3)左、右对应元素(1,4)和(2,4)相等,得: (4) 1 0 ao=0 a3c3-d4s3 c2u -s20-a2, d=0 01 -180-180 a3s3+d4c3=-s2u-C2. (5) 2 -90 a1=120d2=0 02 -170-90 式中:u=CP.+sPy-a1,w=P 3 0 42=220d3=0 -225~70 将(4)和(5)两端平方后相加消去s3、c3,得: 4 -90 43=80d4=20004 -180-180 02=atan2(-v,u)±atan2(√0+h2-m,m). 5 90 a4=0d3=0 -150-150 式中: 6 -90 a3=0 d=0 -180-180 m=写+-2-2-店 运动学正解是已知各关节角度求解机器人末端 -2a2

·158· 智能系统学报 第5卷 若出现2+u2-m2(70180)m (k)],入由第4关节和第6关节许用的最大速度确 2)求解04、05、06 定.04(k+1)表示84目标角度04(k)表示04的当前 由8T=9T8T得: 角度,其余类似。 2T=(8T)18r 至此,求出了全部的01、02、03、04、05、06 (6) 上述求解过程用双变量反正切函数atan2(y, 左边: x)表示角度,求解过程使用了以下结论: CAC5C6 -C4C5S6 -S4C6 -C4S5 若cos0=b,则0=atan2(±√1-b,b)(原文 SsC6 -S586 Cs d -S4C5C6 -C4S6 S4C5S6 -C4C6 S4S5 0 献中为0=atan2(b,±√1-b2),疑为疏误); 0 0 0 1 若acos0+bsin0=0,则0=atan2(a,-b)或 右边: g=atan2(-a,b); 若acos0+bsin0=c,则0=atan2(b,a)±atan2 [ru T12T13 T14 (9T)-18T= T21T22T3 24 (√a2+b+c,c); T31 T32 T33 T34 若as0-koi0=e 6 =atan2(ad -bc,ac +bd) 0 Lasin 0+bcos 0=d' 0 1 式中 3推导结果的讨论 r1l=(C1c2c3-C1s2s3)ng+(s1c2C3-s1s2s3)ny- 3.1角度的表示问题 (s2C3+c2s3)n, 在数学中,y=arcsin(x)的值域是[-T/2, T12=(C1C2c3-Cs2s3)0g+(s1C2C3-S1s23)0y- r/2],y=arccos(x)的值域是[0,r],y=arctan(x) (s2C3+C23)0:, 的值域是(-T/2,π/2),z=atan2(y,x)的值域是 r13=(c1C2c3-c1s23)a.+(s1c2c3-s1s2s3)ay- [-r,π].大多数机器人关节角度是在-180°~ (s2c3+Czs3)a, 180°之间.因此,用双变量反正切函数表示关节角度 r21=(-C1C23-C1s2C3)n-(s1c2s3+s1s2C3)ny+ 更为合适.文献[3,5]直接用反正弦、反余弦、反正 (s2s3-c2c3)n., 切函数表示关节角,而没有考虑实际的机器人关节 22=(-C1C2S3-C1s2C3)0x-(s1C2s3+s1s2C3)0y+ 转动范围,可能造成漏解.对于角度范围超出 -180°~180的关节要分区间讨论. (s2s3-C2C3)02, 3.2增根问题 T23=(-C1c23-C1s2c3)as-(s1c23+s1s2c3)ay+ 通常产生增根的原因有2个:一是解得的目标 (s2s3-c2c3)a, 角度超出机器人关节允许的转动范围;二是代数法 T33 =-s1as +ciay 中运用三角函数公式造成.对于前者,必须通过角度 考虑式(6)左、右对应元素(2,3)相等,得: 范围的校验来别除增根.对于后者,由于不可避免要 0s=atan2(±√1-r2a,r23). 使用三角代换,因此需要借助几何方法来分析可能 若s5≠0,用sigm(s5)表示s5的符号,考虑式(6)两边 的最大逆解组数,以检查推导过程是否引入了增根. 对应元素(1,3)和(3,3)相等,得 若分析得出的最大逆解组数与推导的逆解组数不

第2期 王立权,等:6R关节型机器人运动学建模 ·159· 符,则应继续寻找约束条件,别除增根, 4实验系统及算法检验 本文机器人构型最多有8组逆解,得到8组逆 解,说明代数求解方法没有引入增根. 4.1实验系统 3.3多解问题 根据课题需要,开发了控制系统的软、硬件,图 由第2节推导的结果可知,可能的逆解有8组, 3是机器人实验系统照片.硬件系统以P℃机作为上 如图2所示.实际控制系统只能按其中一组解来执 位机,通过CAN9820总线控制多个下位单片机,每 行,这里采用结构体变量Tree,并引入最佳柔顺准则 个单片机控制一个关节.基于VC+和OpenGL技 式(7)选取惟一解. 术实现机器人的虚拟主从控制,详情见文献[6]. ex=min(公[8(k+)-0,()]) (7) 式中:0(k+1)为目标角度,0(k)为当前角度,k为 权值. 图3机器人系统照片 0. Fig.3 Photo of the robot system 本文所讨论的逆解算法作为算法模块的一个子 0, 程序.由于D-H坐标系设置时将基座、工具形状等 、:4 0e5 因素从核心运动学算法中分离,算法模块可供系统 图2逆解树 中多个机器人共用,并且能够方便地修改其基座位 Fig.2 Tree of inverse solutions 置和工具形状。 Struct Tree/保存逆解的结构体 4.2逆解结果检验 intP://结束标识,初始值为0 利用实验系统可直观地验证逆解结果.为精确 /1,2…表示结束计算的原因 地分析逆解过程,从软件系统中获取运行数据,举例 double thetal; 分析其中一个位姿8T=[1000;010120;001 220;0001],取权值k1=2=k3=1,k4=k5=k6= double theta6;/角度值 0.2.得到的结果如表2所示,与几何方法分析的结 ouble ex; /柔顺值 果一致.图4中给出了4组解,肘关节翻转后可再生 成4组解.表2中加“*”的角度值是参考值(实际 }; 程序中是随机数),最终程序选择了第4组解.将角 具体计算步骤是:计算01→计算02(若2+u2- 度值代人正解表达式,正解结果与给定值一致 m2<0,则P=1,ex=10,结束该组解计算;否则执行 下一步)→判断02是否为增根(若为增根,则P=2, 38.89 82.49° ex=10',结束该组解计算;否则执行下一步)→计算 6.46 67.83 03→判断03是否为增根→计算0→判断0是否为增 3关节Q -151.419 5关节 根→计算0,→计算0。→调用子程序,检验障碍等约束 51.11 -187.51 条件,若不满足则置P值和ex值,否则继续下一步→ 3关节 3关节 计算ex=名k[0,(k+1)-0()].最后,从中选出 -178.56 -148.62 96.429 ex值最小的一组解,并判断ex.若ex<l0',则将该结 2关节 30o-31.38 构体中的角度值作为最终逆解结果,这样就得到了惟 1关 2关节 一逆解.若不满足ex<10',则表明没有可行解,检查 图4机器人的4组解 P值,可以知道原因。 Fig.4 Four solutions of the robot
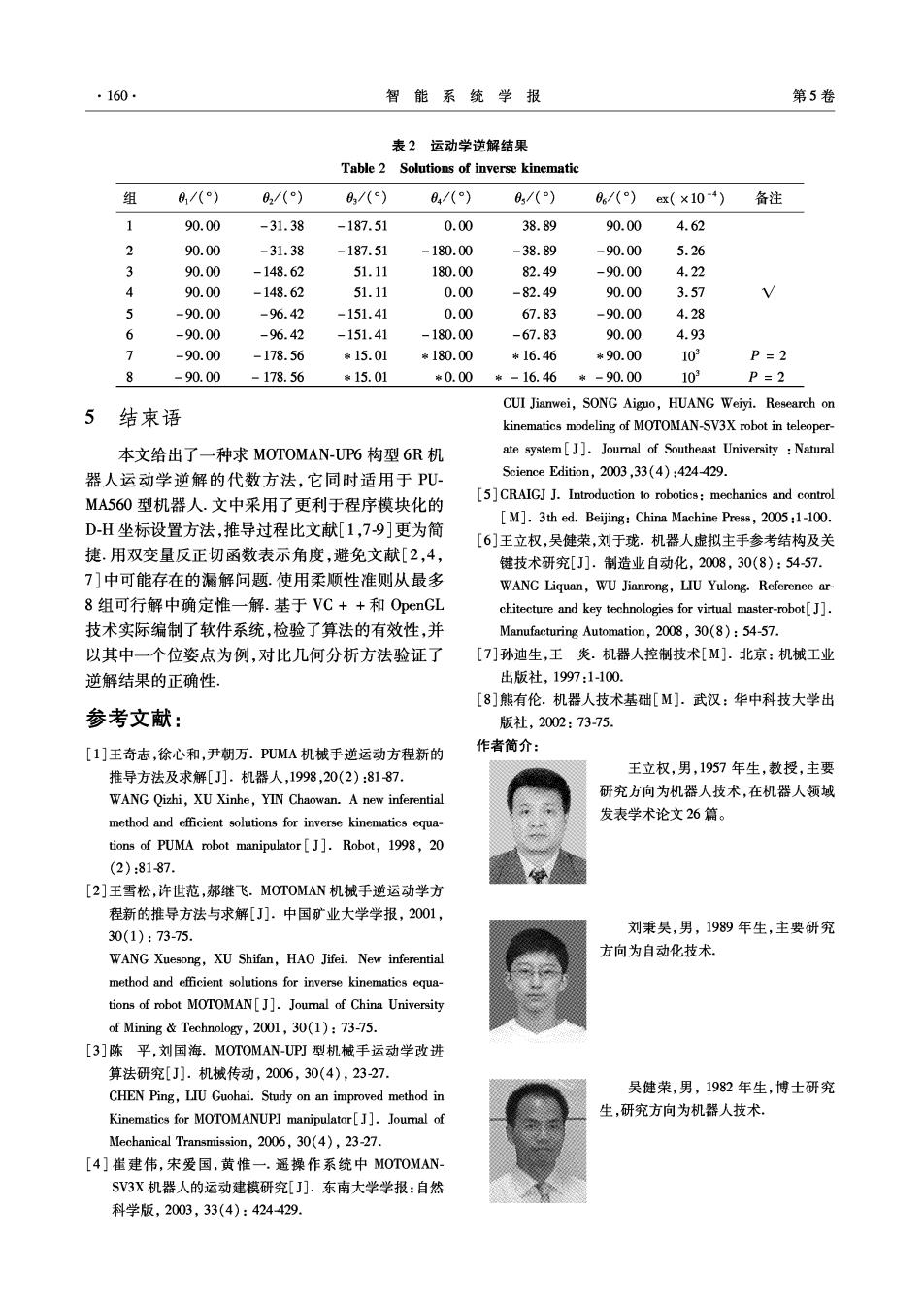
·160. 智能系统学报 第5卷 表2运动学逆解结果 Table 2 Solutions of inverse kinematic 组 9,/() 0,/() 0/() 04/() a/() 0/()ex(×10-4) 备注 1 90.00 -31.38 -187.51 0.00 38.89 90.00 4.62 2 90.00 -31.38 -187.51 -180.00 -38.89 -90.00 5.26 3 90.00 -148.62 51.11 180.00 82.49 -90.00 4.22 4 90.00 -148.62 51.11 0.00 -82.49 90.00 3.57 V 5 -90.00 -96.42 -151.41 0.00 67.83 -90.00 4.28 6 -90.00 -96.42 -151.41 -180.00 -67.83 90.00 4.93 7 -90.00 -178.56 帝15.01 *180.00 *16.46 *90.00 103 P=2 -90.00 -178.56 *15.01 *0.00*-16.46*-90.00 103 P=2 CUI Jianwei,SONG Aiguo,HUANG Weiyi.Research on 5 结束语 kinematics modeling of MOTOMAN-SV3X robot in teleoper- 本文给出了一种求MOTOMAN-UP6构型6R机 ate system[J].Joumal of Southeast University Natural 器人运动学逆解的代数方法,它同时适用于PU Science Edition,2003,33(4):424-429. [5]CRAIGJ J.Introduction to robotics:mechanics and control MA560型机器人.文中采用了更利于程序模块化的 [M].3th ed.Beijing:China Machine Press,2005:1-100. D-H坐标设置方法,推导过程比文献[1,79]更为简 [6]王立权,吴健荣,刘于珑.机器人虚拟主手参考结构及关 捷.用双变量反正切函数表示角度,避免文献[2,4, 键技术研究[J].制造业自动化,2008,30(8):5457. 7]中可能存在的漏解问题.使用柔顺性准则从最多 WANG Liquan,WU Jianrong,LIU Yulong.Reference ar 8组可行解中确定惟一解.基于VC++和OpenGL chitecture and key technologies for virtual master-robot[J]. 技术实际编制了软件系统,检验了算法的有效性,并 Manufacturing Automation,2008,30(8):54-57. 以其中一个位姿点为例,对比几何分析方法验证了 [7]孙迪生,王炎.机器人控制技术[M].北京:机械工业 逆解结果的正确性, 出版社,1997:1-100. [8]熊有伦.机器人技术基础[M].武汉:华中科技大学出 参考文献: 版社,2002:73-75. [1]王奇志,徐心和,尹朝万.PUMA机械手逆运动方程新的 作者简介: 推导方法及求解[J].机器人,1998,20(2):8187. 王立权,男,1957年生,教授,主要 WANG Qizhi,XU Xinhe,YIN Chaowan.A new inferential 研究方向为机器人技术,在机器人领域 method and efficient solutions for inverse kinematics equa- 发表学术论文26篇。 tions of PUMA robot manipulator[J].Robot,1998,20 (2):8187. [2]王雪松,许世范,郝继飞.MOTOMAN机械手逆运动学方 程新的推导方法与求解[J刀.中国矿业大学学报,2001, 刘秉吴,男,1989年生,主要研究 30(1):73-75. WANG Xuesong,XU Shifan,HAO Jifei.New inferential 方向为自动化技术 method and efficient solutions for inverse kinematics equa- tions of robot MOTOMAN[J].Journal of China University of Mining Technology,2001,30(1):73-75. [3]陈平,刘国海.MOTOMAN-UPJ型机械手运动学改进 算法研究[J].机械传动,2006,30(4),23-27 CHEN Ping,LIU Guohai.Study on an improved method in 吴健荣,男,1982年生,博士研究 Kinematics for MOTOMANUPJ manipulator[J].Journal of 生,研究方向为机器人技术 Mechanical Transmission,2006,30(4),23-27. [4]崔建伟,宋爱国,黄惟一.遥操作系统中MOTOMAN SV3X机器人的运动建模研究[J].东南大学学报:自然 科学版,2003,33(4):424429